1.8 Динамика адсорбции

В основе расчета процессов очистки промышленных выбросов и сточных вод лежат закономерности динамики адсорбции. Динамика адсорбционных процессов рассматривает пространственно-временные распределения компонентов между фазами системы, возникающие при перемещении фаз относительно друг друга.

Рассмотрим процесс в колонке, заполненной адсорбентом, причем для удобства анализа примем горизонтальное расположение колонки, в которую подается поток очищаемого газа или жидкости. Проследим за изменением концентрации адсорбирующегося компонента в обеих фазах при условии постоянства во времени концентрации адсорбтива в очищаемом потоке и равенстве концентрации адсорбата в исходном адсорбенте нулю. В начальный момент процесса адсорбент начинает поглощать адсорбтив лобовым слоем адсорбента, причем концентрация адсорбтива в потоке убывает. Частично истощенная по адсорбтиву порция газа далее поступает в следующий слой. В нем начинают проходить процессы поглощения. Рассмотрим процесс в различные промежутки времени (рис. 1.11).

Рис. 1.11. Формирование и перемещение фронта адсорбции по гори- зонтальному адсорберу

В период времени количество поступившего адсорбтива еще недостаточно для насыщения лобового слоя адсорбента и распределение адсорбата в слое характеризуется кривой . При времени процесса > лобовой слой насыщается адсорбатом до величины равновесной адсорбции (емкости). Распределение концентрации вещества в любой из фаз, достигнутое ко времени , называют фронтом сорбции. После этого момента кривая распределения сорбата перемещается с постоянной скоростью U, которая вычисляется по формуле:

, (1.27)

где – скорость потока; С₀ – концентрация адсорбтива; – равновесная адсорбционная емкость.

В период слой адсорбента можно разделить на три зоны: полностью отработанный слой L₁, работающий слой L₀ и еще не вступивший в работу слой L₂. В момент времени кривая распределения перемещается в концевой слой адсорбента. С этого момента – момента "проскока" – в выходящем потоке газа (жидкости) появляется и начинает прогрессивно возрастать концентрация извлекаемого компонента, , причём – время проскока или время защитного действия слоя адсорбента.

Для обеспечения высокой степени очистки перед наступлением "проскока" адсорбер переключают на регенерацию, но при этом часть емкости загруженного в аппарат адсорбента не используется. Степень недоиспользования емкости работающего слоя характеризуют коэффициентом симметричности φ, который определяют из соотношения площадей (рис. 1.11) .

Количество вещества, поглощенное до момента проскока и отнесенное к массе загрузки адсорбера, называют динамической адсорбционной емкостью. Степень использования адсорбционной емкости слоя может быть определена отношением динамической адсорбционной емкости к равновесной величине, т.е. . Величина определяется соотношением высоты слоя адсорбента L и высоты работающего слоя L₀:

. (1.28)

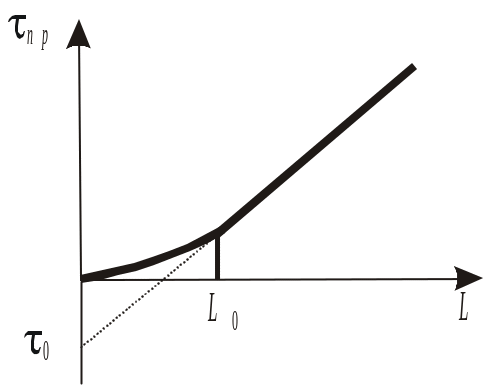
Процесс адсорбции принято характеризовать уравнением Шилова:

, (1.29)

где k – коэффициент защитного действия, показывающий, какое время слой адсорбента толщиной 1 см задерживает поглощаемое вещество до требуемой концентрации в стационарном режиме; – потеря времени защитного действия, связанная с начальным периодом формирования кривой распределения адсорбата.

Для понимания сущности процесса и применимости уравнения Шилова удобно использовать график, приведенный на рис. 1.12.

Коэффициент защитного действия слоя – величина, обратная скорости движения сорбционного фронта (сорбционной волны) .

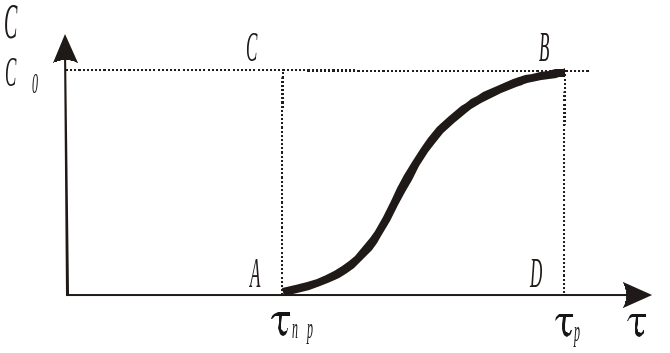
Рис. 1.12. Зависимость времени защитного действия слоя от его длины L	Рис. 1.13. Выходная кривая при погло- щении примеси из потока в непод- вижном слое адсорбента

При экспериментальном исследовании процессов адсорбции обычно снимают выходную кривую (рис. 1.13). По выходной кривой определяют величину работающего слоя L₀, отражающую нарастание концентрации примесей за слоем адсорбента во времени:

, (1.30)

где – разность времени между появлением исходной концентрации компонента на выходе и проскоковой концентрацией за слоем; – время появления максимальной концентрации; φ – коэффициент симметричности выходных кривых или кривых распределения.

Рассмотренные закономерности динамики процессов адсорбции характерны (с достаточной достоверностью) при поглощении одного компонента потока, при несжимаемости подвижной фазы. В этом случае можно пренебречь изменениями плотности потока по длине слоя из-за убыли адсорбтива при перемещении потока в одном направлении. Для полного описания динамики адсорбции в реальных условиях необходима система уравнений материального и теплового балансов, кинетики адсорбции и теплопередачи, уравнения изотерм адсорбции. Более сложные случаи неизотермической адсорбции, адсорбции в нестационарных режимах, адсорбции нескольких компонентов рассмотрены в специальных монографиях.

При очистке промышленных выбросов и сбросов используются в основном периодические процессы, проводимые в аппаратах с неподвижным слоем адсорбента. После окончания очистки, определяемой исчерпанием емкости адсорбента, аппарат переключают на десорбцию. В рабочий цикл могут включать ряд дополнительных операций: сушку и охлаждение адсорбента, повышение и сброс давления и т.д. В последние десятилетия развиваются процессы с движущимся или псевдоожиженным слоем адсорбента. Эти процессы отличаются более высокими скоростями, но требуют от адсорбентов повышенной механической прочности. Какой тип аппарата использовать в конкретном случае решается, исходя из объема очищаемого потока, его состава, требований к очистке, наличия надлежащего сорбента, экономических соображений.

0