1.4. Теория объемного заполнения микропор

Адсорбционные явления, протекающие на поверхности мезо-, макропор и в микропорах принципиально отличаются. Теории физической адсорбции при всем их различии рассматривают процесс как поглощение одного или нескольких последовательных слоев адсорбата на геометрической поверхности адсорбента. Микропоры представляют как области пространства в твердом теле, размеры которых соизмеримы с размерами адсорбируемых молекул. В таком случае при любой природе адсорбционных взаимодействий, обусловливающих физическую адсорбцию, во всем пространстве микропор проявляется адсорбционное поле, создаваемое твердым телом. Ограниченность адсорбционного пространства микропор предопределяет тот факт, что последовательно адсорбирующиеся в микропорах молекулы не образуют адсорбционных слоев. Адсорбция в микропорах характеризуется объемным заполнением микропор. Отсюда основным геометрическим параметром, характеризующим микропористые адсорбенты, является объем микропор, а не их поверхность.

Для микропор введено понятие величины предельной (максимальной) адсорбции А₀, которая соответствует адсорбции пара при давлении, равном давлению насыщенного пара. Величина А₀ зависит от температуры, и эта зависимость определяется термическим коэффициентом предельной адсорбции , который практически постоянен в широком интервале температур:

. (1.18)

Адсорбированное вещество в микропорах в поле адсорбционных сил подобно жидкости, находящейся в сильно сжатом состоянии. В области температур значительно ниже критических плотность адсорбата в первом приближении можно принять равной плотности поглощаемого вещества в жидком состоянии при температуре опыта. Более точные зависимости реальных плотностей адсорбата при разных температурах приведены в специальной литературе. Допущение о том, что плотность адсорбата соответствует плотности сжиженного пара при температуре опыта, облегчает практические расчеты, но имеет смысл только для р = р_s и поэтому не всегда точно выполняется.

В практических расчетах для адсорбентов разной структуры широкое распространение получило степенное уравнение адсорбции Фрейндлиха:

, (1.19)

где А – количество адсорбированного вещества; р – давление адсорбтива; k и n – постоянные величины.

Простота и удовлетворительное описание экспериментальных данных в широком интервале давлений, за исключением интервала очень низких давлений, когда адсорбция описывается уравнением Генри, способствовали широкому распространению уравнения Фрейндлиха.

В расчетах адсорбционных процессов часто используют линейную форму уравнения:

Рис. 1.8. Изотермы адсорбции в координатах уравнения Фрейндлиха

. (1.20)

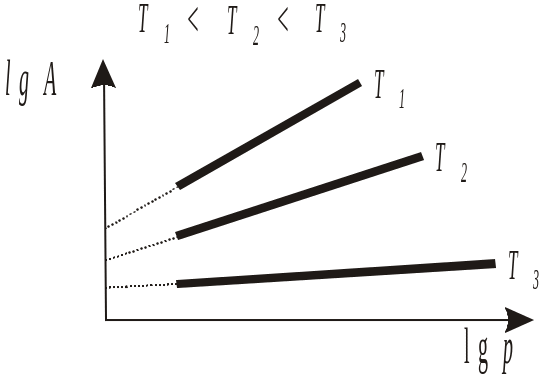
Изотермы адсорбции в координатах lg А-lg р изображаются прямой линией. Тангенс угла наклона прямых позволяет определять величину коэффициента n (рис. 1.8), а отрезки, отсекаемые ими на оси ординат, – lg k. С понижением температуры величина n последовательно увеличивается, приближаясь к предельному значению, равному 1. В предельном случае (низкая адсорбционная способность) адсорбционное равновесие аналогично процессу растворения и подчиняется закону Генри: адсорбция линейно растет с повышением давления. Значения k с ростом температуры уменьшаются.

Для пара уравнение Фрейндлиха является частным случаем более общего уравнения изотермы адсорбции теории объемного заполнения микропор:

, (1.21)

где Е – характеристическая энергия адсорбции.

Если принять, что k = А₀, а n = 0,434RT/E, то последнее уравнение совпадает с уравнением (1.20), что подтверждает сказанное выше.