
- •Индивидуальные задания для зачета по Матлогике
- •1. Полностью определенные булевы функции. Днф и кнф
- •2. Определить сднф, скнф, мднф для функции, заданной вектором:
- •2. Минимизация частично определенных булевых функций
- •1. Найти мднф для функции, заданной вектором:
- •2. Найти мднф для частично определенной булевой функции методом таблиц различий и методом симметричных таблиц. Сравнить результаты.
- •3. Метод резолюций в логике высказываний
- •4. Элементы теории алгоритмов
- •2 По заданной машине Тьюринга т и начальной конфигурации к1 найти заключительную конфигурацию (q0 * заключительное состояние).
- •3. Построить композицию т1т2 машин Тьюринга т1 и т2 (по паре состояний (q10, q21)) и найти результат применения композиции t1t2 к слову p (q20 - заключительное состояние машины т2), если
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
Тверской Государственный Технический Университет
(ТвГТУ)
Факультет ИДПО
Кафедра: «Электронно-вычислительных машин»
Направление 230100: « Информатика и вычислительная техника »
КОНТРОЛЬНАЯ работа
по дисциплине:
«Математической логике»
Выполнил: |
студент группы ИВТ – 226 |
|
Михайлов М. А. |
Проверила: |
Асеева Т. В. |
Тверь
Индивидуальные задания для зачета по Матлогике
№ п/п |
1. Функции алгебры логики |
2. Минимизация булевых функций |
3 Метод резолюций |
4. Машина Тьюринга |
21 |
1.4, 2.1 |
1.21, 2.10 |
1.18, 1.2 |
1.1c, 2.2a, 3.1a, 6 |
1. Полностью определенные булевы функции. Днф и кнф
1. Построить таблицу истинности для формулы и, используя правила равносильных преобразований формул, привести ее к ДНФ и к КНФ. Проверить правильность выполненных преобразований с использованием диаграмм Вейча.
1.4. (x(x˄y)) z;
x |
y |
z; |
x˄y |
(x(x˄y)) |
(x(x˄y)) z |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
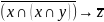 ;
;
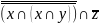 ;
;
 ;
;
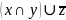 -ДНФ;
-ДНФ;
 -КНФ;
-КНФ;
СДНФ -
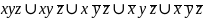
СКНФ -
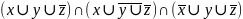
Диаграмма Вейча
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
 ;
;
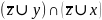 ;
;
2. Определить сднф, скнф, мднф для функции, заданной вектором:
2.1. f= ( 1001 0110 1011 0011);
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
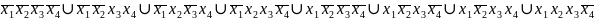 - СДНФ
- СДНФ
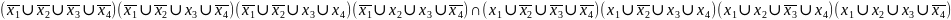 -
СКНФ
-
СКНФ
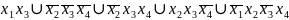 - МДНФ
- МДНФ
2. Минимизация частично определенных булевых функций
1. Найти мднф для функции, заданной вектором:
1.21 f=(*0** 0*11 1*** 000*);
0 |
0 |
* |
1 |
0 |
* |
* |
* |
1 |
1 |
* |
* |
0 |
* |
0 |
* |
МДНФ -
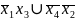
2. Найти мднф для частично определенной булевой функции методом таблиц различий и методом симметричных таблиц. Сравнить результаты.
2.10. N1= (0*0*01*)(0*1**11)(000**11); N0=(*0101**)(*10011*)(1***000);
0*0*01* |
|
0*1**11 |
|
000**11 |
|
0000010 |
02 |
0010011 |
23 |
0000011 |
03 |
0000011 |
03 |
0010111 |
27 |
0000111 |
07 |
0001010 |
12 |
0011011 |
33 |
0001011 |
13 |
0001011 |
13 |
0011111 |
37 |
0001111 |
17 |
0100010 |
42 |
0110011 |
63 |
|
|
0100011 |
43 |
0110111 |
67 |
|
|
0101010 |
52 |
0111011 |
73 |
|
|
0101011 |
53 |
0111111 |
77 |
|
|
*0101** |
|
*10011* |
|
1***000 |
|
0010100 |
24 |
0100110 |
46 |
1000000 |
00 |
0010101 |
25 |
0100111 |
47 |
1001000 |
10 |
0010110 |
26 |
1100110 |
46 |
1010000 |
20 |
0010111 |
27 |
1100111 |
47 |
1011000 |
30 |
1010100 |
24 |
|
|
1100000 |
40 |
1010101 |
25 |
|
|
1101000 |
50 |
1010110 |
26 |
|
|
1110000 |
60 |
1010111 |
27 |
|
|
1111000 |
70 |
|
0 |
1 |
|||||||||||||||
y2y1 |
0 |
1 |
3 |
2 |
6 |
7 |
5 |
4 |
4 |
5 |
7 |
6 |
2 |
3 |
1 |
0 |
|
0 |
* |
* |
1 |
1 |
* |
1 |
* |
* |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
* |
* |
1 |
1 |
* |
1 |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
|
3 |
* |
* |
1 |
* |
* |
1 |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
|
2 |
* |
* |
1 |
* |
0 |
* |
0 |
0 |
0 |
0 |
0 |
0 |
* |
* |
* |
* |
|
6 |
* |
* |
1 |
* |
* |
1 |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
|
7 |
* |
* |
1 |
* |
* |
1 |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
|
5 |
* |
* |
1 |
1 |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
* |
|
4 |
* |
* |
1 |
1 |
0 |
0 |
* |
* |
* |
* |
0 |
0 |
* |
* |
* |
* |
|
МДНФ -

|
|
*0101** |
*10011* |
1***000 |
X7 |
0 |
0 |
0 |
1 |
X6 |
* |
0 |
0 |
0 |
X5 |
0 |
1 |
0 |
0 |
X4 |
* |
0 |
0 |
0 |
X3 |
0 |
1 |
1 |
0 |
X2 |
1 |
0 |
0 |
1 |
X1 |
* |
0 |
0 |
0 |
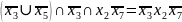
|
|
*0101** |
*10011* |
1***000 |
X7 |
0 |
0 |
0 |
1 |
X6 |
* |
0 |
0 |
0 |
X5 |
1 |
0 |
1 |
0 |
X4 |
* |
0 |
0 |
0 |
X3 |
* |
0 |
0 |
0 |
X2 |
1 |
0 |
0 |
1 |
X1 |
1 |
0 |
0 |
1 |
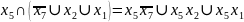
|
|
*0101** |
*10011* |
1***000 |
X7 |
0 |
0 |
0 |
1 |
X6 |
0 |
0 |
1 |
0 |
X5 |
0 |
1 |
0 |
0 |
X4 |
* |
0 |
0 |
0 |
X3 |
* |
0 |
0 |
0 |
X2 |
1 |
0 |
0 |
1 |
X1 |
1 |
0 |
0 |
1 |
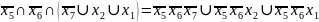
N1 Imax |
0*0*01* |
0*1**11 |
000**11 |
|
+ |
- |
- |
|
- |
+ |
- |
|
- |
- |
+ |
МДНФ -
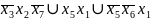
Ответ: МДНФ методом симметричных таблиц
МДНФ методом таблиц различий

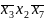 (0***01*)
(0***01*)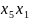 (**1***1)
(**1***1)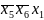 (*00***1)
(*00***1)