
- •Множества. Точка. Операции над множествами. Алгебра множеств. Множества с заданными на них операциями. Алгебраические структуры: группа, кольцо, поле. Поле комплексных чисел.
- •Матрицы. Определитель. Их свойства и вычисления.
- •Решение слау методом Крамера.
- •Миноры матрицы. Ранг матрицы. Элементарные преобразования матрицы.
- •Арифметическое пространство строк. Линейная зависимость. Свойство линейной зависимости. Теорема о базисном миноре.
- •Теорема о совместности. Произвольные слау.
- •Метод Гаусса
- •Линейные пространства. Примеры, определение. Базис линейного пространства, размерности, разложение векторов в пространстве
- •Основные понятия аналитической геометрии. Векторная алгебра. Скалярное, векторное и смешанное произведение векторов.
- •Плоскость в пространстве.
- •Прямая линия в пространстве и на плоскости.
- •Эллипс, гипербола и параболы.
- •Поверхности: цилиндры, поверхности, вращение, эллипсоид, гиперболоид, параболоид, конусы второго порядка.
- •Теоремы последовательностей.
- •Основные элементарные функции, пределы функций, теоремы о пределе.
- •1Ый и 2ой замечательный предел.
- •Непрерывность функций и классификация. Теорема о непрерывн. Функции в точке. Теорема о непрерывн. Функциях в отрезках.
- •Производная функции в точке. Дифференцируемость и непрерывность. Таблица производных. Правило дифференцирования.
- •Производная сложной функции. Таблица производных. Производная функции задана не явно. Логарифм дифференциала. Производная функции заданной параметрически.
- •Обратная функция
- •Исследование функции. Построение графиков.
- •Метод Ньютона
- •Метод Симпсона.
Ответы на математику
Множества. Точка. Операции над множествами. Алгебра множеств. Множества с заданными на них операциями. Алгебраические структуры: группа, кольцо, поле. Поле комплексных чисел.
Множество - совокупность различных элементов, мыслимая как единое целое. Множество может быть замкнутым и незамкнутым, полным и пустым, упорядоченным и неупорядоченным, счётным и несчётным, конечным и бесконечным. В математике то́чкой называют абстрактный объект в пространстве, не имеющий ни объёма, ни площади, ни длины, ни каких-либо других измеримых характеристик. Точка является одним из фундаментальных понятий в математике; любая геометрическая фигура считается состоящей из точек.
Операции над множествами:
Множества
обозначаются заглавными латинскими
буквами, а их элементы – строчными.
Запись a ![]() R означает,
что элемент а принадлежит
множеству R ,
то есть а является
элементом множества R .
В противном случае, когда а не
принадлежит множеству R ,
пишут a
R означает,
что элемент а принадлежит
множеству R ,
то есть а является
элементом множества R .
В противном случае, когда а не
принадлежит множеству R ,
пишут a ![]() R .
R .
Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А .
Говорят,
что множество А содержится
в множестве В ( рис.1 )
или множество А является подмножеством множества В ( в
этом случае пишут А ![]() В), если
каждый элемент множества А одновременно
является элементом множества В .
Эта зависимость между множествами
называется включением.
Для любого множества А имеют
место включения:
В), если
каждый элемент множества А одновременно
является элементом множества В .
Эта зависимость между множествами
называется включением.
Для любого множества А имеют
место включения: ![]() А
и А
А .
А
и А
А .


Сумма
( объединение )
множеств А и В ( пишется А ![]() В )
есть множество элементов, каждый из
которых принадлежит либо А ,
либо В.
Таким образом, е
А
В тогда
и только тогда, когда либо
е
А , либо е
В .
В )
есть множество элементов, каждый из
которых принадлежит либо А ,
либо В.
Таким образом, е
А
В тогда
и только тогда, когда либо
е
А , либо е
В .
Произведение
( пересечение )
множеств А и В ( пишется А ![]() В ,
рис.2 ) есть множество элементов,
каждый из которых принадлежит и А ,
и В .
Таким образом, е
А
В тогда
и только тогда, когда е
А и е
В .
В ,
рис.2 ) есть множество элементов,
каждый из которых принадлежит и А ,
и В .
Таким образом, е
А
В тогда
и только тогда, когда е
А и е
В .
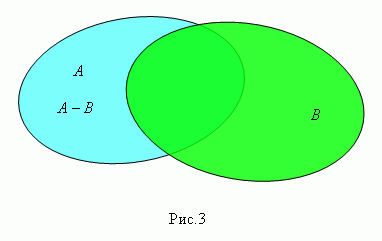
Разность множеств А и В ( пишется А – В , рис.3 ) есть множество элементов, которые принадлежат множеству А , но не принадлежат множеству В.Это множество называется также дополнением множества В относительно множества А.
Симметричная разность множеств А и В ( пишется А \ В ) есть множество:
А \ В = ( А – В ) ( В – А ).
Свойства операций над множествами:

Множества с заданными на них операциями называются алгебраической структурой.
Непустое
множество ![]() с
заданной на нём бинарной
операцией
с
заданной на нём бинарной
операцией ![]() называется
группой
называется
группой ![]() ,
если выполнены следующие аксиомы:
,
если выполнены следующие аксиомы:
ассоциативность:
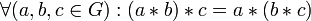 ;
;наличие нейтрального элемента:
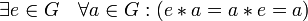 ;
;наличие обратного элемента:
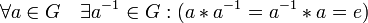
Примерами групп являются действительные числа с операцией сложения, множество вращений плоскости вокруг начала координат и т. п.
Кольцо — это множество R, на котором заданы две бинарные операции: + и × (называемые сложение и умножение), со следующими свойствами:
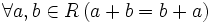 — коммутативность сложения;
— коммутативность сложения;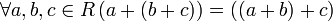 — ассоциативность сложения;
— ассоциативность сложения;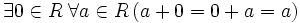 —
существование
нейтрального элемента относительно
сложения;
—
существование
нейтрального элемента относительно
сложения;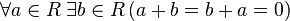 —
существование
противоположного элемента относительно
сложения;
—
существование
противоположного элемента относительно
сложения;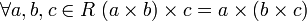 —
ассоциативность
умножения (некоторые авторы не требуют
выполнения этой аксиомы[1])
—
ассоциативность
умножения (некоторые авторы не требуют
выполнения этой аксиомы[1])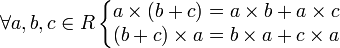 — дистрибутивность.
— дистрибутивность.
Простейшими примерами колец являются алгебры чисел (целых,вещественных, комплексных, …), функций на множестве (всех, непрерывных, гладких, аналитических, …) и матриц.
По́лем называется множество F с
двумя бинарными
операциями ![]() (сложение)
и
(сложение)
и ![]() (умножение),
если оно (вместе с этими операциями)
образует коммутативное ассоциативное кольцо c
единицей
(умножение),
если оно (вместе с этими операциями)
образует коммутативное ассоциативное кольцо c
единицей ![]() ,
все ненулевые элементы которого обратимы.
,
все ненулевые элементы которого обратимы.
Примеры поля: рациональные числа, вещественные, комплексные.
Ко́мпле́ксные[1] чи́сла —
расширение поля вещественных
чисел,
обычно обозначается ![]() .
Любое комплексное число может быть
представлено как формальная сумма
.
Любое комплексное число может быть
представлено как формальная сумма ![]() ,
где
,
где ![]() и
и ![]() —
вещественные числа,
—
вещественные числа, ![]() — мнимая
единица.
— мнимая
единица.
