
- •1. Назначение экономико-математических моделей (эмм). Два принципа их спецификации. Типы уравнений в эмм: поведенческие уравнения и тождества (на примере макромодели).
- •2. Типы переменных в экономических моделях. Структурная и приведённая форма модели (на примере макромодели). Компактная запись.
- •4. Спецификация и преобразование к приведённой форме эконометрических моделей. Эконометрическая модель Самуэльсона–Хикса делового цикла экономики. Компактная запись.
- •Порядок оценивания линейной эконометрической модели из изолированного уравнения в Excel. Смысл выходной статистической информации функции линейн.
- •Случайная переменная и закон её распределения. Нормальный закон распределения и его параметры.
- •Случайная переменная и закон её распределения. Распределение хи-квадрат.
- •Случайная переменная и закон её распределения. Распределение Стьюдента, Квантиль, t крит уровня и её расчёт в Excel.
- •Ковариация Cov(X, y), и коэффициент корреляции, Cor(X, y) пары случайных переменных (X, y). Частная ковариация и частный коэффициент корреляции.
- •Свойства
- •Случайная переменная и закон её распределения. Закон распределения Фишера. Квантиль, f крит уровня и её расчёт в Excel.
- •Случайный вектор и его основные количественные характеристики (на примере вектора левых частей схемы Гаусса – Маркова при гомоскедастичном неавтокоррелированном остатке).
- •Случайный вектор и факторизация его ковариационной матрицы. Случайный вектор случайных остатков в схеме Гаусса – Маркова при гетероскедастичном неавтокоррелированном остатке.
- •Временной ряд и его структура (На примере ввп России).
- •Модели тренда временного ряда.
- •17. Моделирование сезонной составляющей при помощи фиктивных переменных.
- •18. Регрессионная зависимость случайных переменных. Функция регрессии, стандартные модели функции регрессии.
- •19.Схема Гаусса–Маркова (на примере модели Оукена).
- •20.Понятие статистической процедуры оценивания параметров эконометрической модели. Линейные статистические процедуры. Требования к наилучшей статистической процедуре.
- •29.Свойства мнк-оценок параметров линейной модели множественной регрессии (лммр) при нормальном векторе случайных остатков: независимость случайных векторов
- •30.Свойства мнк-оценок параметров линейной модели множественной регрессии (лммр) при нормальном векторе случайных остатков: закон распределение оценки .
- •31. Свойства мнк-оценок параметров линейной модели множественной регрессии (лммр) при нормальном векторе случайных остатков: закон распределения дроби .
- •32. Оценивание параметров линейной модели множественной регрессии (лммр) при нормальном векторе случайных остатков методом максимального правдоподобия (ммп).
- •34. Спецификация и оценивание нелинейных по коэффициентам моделей множественной регрессии со специальными функциями регрессии (на примере производственной модели с функцией Кобба-Дугласа).
- •35. Оптимальное точечное прогнозирование значений эндогенной переменной по линейной модели (случай гомоскедастичного и неавтокоррелированного случайного остатка) на примере модели Оукена.
- •Тест Голдфелда-Квандта гомоскедастичности случайного остатка в лммр
- •37.Тест Дарбина–Уотсона отсутствия автокорреляции случайного остатка в лммр.
- •38.Коэффициент детерминации как мерило качества спецификации эконометрической модели (на примере модели Оукена). Скорректированный коэффициент детерминации.
- •39. Связь коэффициента детерминации с коэффициентом корреляции эндогенной переменной и её оценки (на примере модели Оукена).
- •41. Процедура интервального прогнозирования по оценённой линейной эконометрической модели значений эндогенной переменной (на примере модели Оукена).
- •42.Процедура проверки адекватности оценённой линейной эконометрической модели (на примере модели Оукена).
- •43.Последствия, симптомы и методика устранения ошибки спецификации эконометрической модели, состоящей в неверном выборе функции регрессии.
- •44.Последствия и симптомы ошибки спецификации линейной эконометрической модели, состоящей во включении незначимой объясняющей переменной.
- •45. Последствия и симптомы ошибки спецификации линейной эконометрической модели, состоящей в пропуске значимой объясняющей переменной.
- •46. Последствия и симптомы ошибки спецификации линейной эконометрической модели, состоящей в непостоянстве значений её параметров в области изменения объясняющих переменных; тест Чоу.
- •47. Основные характеристики временного ряда.
- •48. Стационарный временной ряд. Белый шум.
- •49.Оценка характеристик стационарного временного ряда.
- •Частная автокорреляционная функция стационарного временного ряда и алгоритм её оценивания.
- •Модель ar(p) и её идентификация.
- •Модель ma(q) и её идентификация.
- •Оптимальный линейный алгоритм прогнозирования уровней стационарного временного ряда.
- •Модели нестационарных временных рядов. Идентификация модели тренда.
- •Оценивание линейной модели с автокоррелированным остатком ar(1) алгоритмом Хильдретта – Лу.
- •Проблема мультиколлинеарности, типы и симптомы мультиколлинеарности. Методика отбора регрессоров в линейной модели в ситуации мультиколлинеарности.
- •Эконометрические модели в виде систем линейных одновременных уравнений (слоу): примеры и проблема идентификации (на примере модели спроса-предложения блага).
- •Эконометрические модели в виде систем линейных одновременных уравнений (слоу): примеры и проблема оценивания параметров структурной формы (на примере макромодели Кейнса).
- •Необходимое условие идентифицируемости поведенческого уравнения модели слоу (правило порядка). Сверхидентифицируемость параметров поведенческого уравнения.
- •60. Необходимое условие идентифицируемости поведенческого уравнения модели слоу (правило порядка)
- •61. Критерий идентифицируемости поведенческого уравнения модели слоу (правило ранга)
- •62. Понятие инструментальных переменных. Оценивание параметров структурной формы двухшаговым м-ом наименьших квадратов на примере простейшей макромодели Кейнса
- •63. Теорема Слуцкого и оценивание параметров структурной формы косвенным методом наименьших квадратов (кмнк) – на примере простейшей макромодели Кейнса.
Порядок оценивания линейной эконометрической модели из изолированного уравнения в Excel. Смысл выходной статистической информации функции линейн.
У нас построена линейная эконометрическая
модель с изолированными переменными:
нас построена линейная эконометрическая
модель с изолированными переменными:
Рассмотрим спецификацию данного вида.
В этой модели экзогенных переменных х1 и х2 и одна эндогенная переменная уt. Случайное возмущение u предполагается гомоскедастичным. Спецификация содержит 4 параметра: а0, а1, а2, .
Модели данного типа называются линейными эконометрическими моделями в виде изолированных уравнений с несколькими объясняющими переменными или линейной множественной регрессии.
Порядок оценивания модели состоит в следующем:
Ввести исходные данные или открыть из существующего файла, содержащего анализируемые данные;
В данном случае выделяем область пустых ячеек 5*3 (5 строк, 3 столбца) для вывода результатов регрессионной статистики (функция линейн).
В общем случае: подготавливаем область, состоящую всегда из 5 строк, а столбцов столько, сколько коэффициентов требуется оценить, но минимум 2( а0, а1) .
Активизировать Мастер функций любым из способов:
В главном меню выбрать Вставка/Функция
На панели инструментов Стандартная щелкнуть на кнопке Вставка функции;
В окне Категория выбрать Статистические, в окне Функция – ЛИНЕЙН, щелкнуть ОК;
Заполнить аргументы функции:
Известные значения y – диапазон, содержащий данные результативного признака;
Известные значения x – диапазон, содержащий данные факторов независимого признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении. Если Константа =1, то свободный член рассчитывается обычным образом, если Константа=0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию или нет. Если статистика =1, то дополнительная информация выводится, если Статистика =0, то выводятся только оценки параметров уравнения.
Нажать комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.
Щелкнуть ОК.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
a2~ |
a1~ |
a0~ оценка коэффициента |
S(a2~) |
S(a1~) |
S(a0~) стандартные ошибки |
R^2 доля дисперсии эндогенной переменной, объясн. уравнением регрессии |
|
Н/Д |
F статистика Фишера, предназначенная для проверки статической значимости коэф. детерминации |
υ2 стемени свободы |
Н/Д |
|
|
Н/Д |
Случайная переменная и закон её распределения. Нормальный закон распределения и его параметры.
Переменная
величина x
c
областью изменения X
называется случайной, если свои возможные
значения q
из множества X
она принимает в результате некоторого
опыта со случайными элементарными
исходами вида
 .
.
x-
дискретная случайная переменная, если
множество Х состоит из конечного или
счетного количества констант
 .
.
З-н
распределения дискретной случайной
переменной- функция
 скалярного аргумента q
с областью определения
скалярного аргумента q
с областью определения
 ,
характеризующая возможность появления
в опыте значений q
случайной переменной x.
,
характеризующая возможность появления
в опыте значений q
случайной переменной x.
З-н
распределения дискретной случайной
переменной называется вероятностной
функцией, значение которой равны
вероятностям появления в опыте возможного
значения сл. переменной:
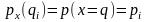
Нормальный закон распределения случайной величины имеет вид (НормРаспр, НормОбр):

параметры: математическое ожидание m и среднее квадратическое отклонение - сигма.
Нормальный закон возникает тогда, когда случайная переменная х формируется под воздействием большого числа независимых факторов.

 оценка
среднего квадратичного отклонения
остатка (оценка случайного возмущения)
оценка
среднего квадратичного отклонения
остатка (оценка случайного возмущения) регрессионная
сумма квадратов
регрессионная
сумма квадратов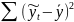 остаточная
сумма квадратов
остаточная
сумма квадратов