8. Линейная комбинация векторов и разложение вектора по системе векторов

Линейной комбинацией векторов с коэффициентами называется вектор , в этом случае говорят так же, что вектор разложен по системе векторов , а числа являются коэффициентами разложения.

Пример 1. Дана система векторов

, , .

Найти линейную комбинацию: .

Решение. 2·(2; 3; 6; -10)-(-2; 4; 0; -5)+3·(1; 5; -1; 3)+0·(-1; 2; -2; 3)=(4; 6; 12; -20)-(-2; 4; 0; -5)+(3; 15; -3; 9)+(0; 0; 0; 0)=(4+2+3+0; 6-4+15+0; 12-0-3+0; -20+5+9+0)=(9; 17; 9; -6)

Вектор разлагается по системе векторов , и коэффициентами разложения являются числа: λ₁=2; λ₂=-1; λ₃=3; λ₄=0.

С помощью векторов удобно записывать систему уравнений:

Введем в рассмотрение векторы-столбцы:

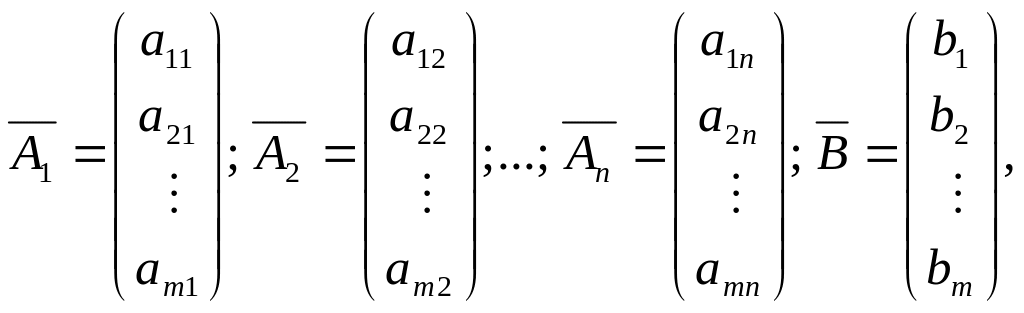
Тогда систему можно записать так:

или

Если совокупность чисел является решением системы (1.2), то вектор разлагается по векторам , и коэффициентами разложения являются числа , т.е. справедливо соотношение: .

Таким образом, чтобы найти разложение вектора по системе векторов достаточно найти любое решение системы уравнений: .

9. Линейно-зависимые и линейно независимые системы векторов

Система векторов называется линейно-зависимой, если можно подобрать такие числа , , . . . , не все равные нулю (есть ≠0), что

( - нуль-вектор)

Система векторов называется линейно-независимой, если из данных векторов нельзя составить нулевую линейную комбинацию с отличными от нуля коэффициентами, т.е. для линейно-независимой системы векторов выражение (1.3) справедливо тогда, когда все коэффициенты =0, .

Справедливы следующие утверждения.

Лемма. Если часть системы векторов линейно-зависима, то и вся система векторов линейно-зависима.

Теорема 1. Если система векторов линейно-зависима, то хотя бы один из них можно представить в виде линейной комбинации остальных векторов.

Следствие 1. Если хотя бы один вектор системы линейно выражается через остальные векторы, то система линейно-зависима.

Следствие 2. В линейно-независимой системе ни один из векторов нельзя выразить через остальные.

Теорема 2: Если каждый из векторов системы линейно выражается через векторы (k<m), то система векторов линейно зависима.

Теорема 3: В n-мерном пространстве любая система, содержащая более чем n векторов линейно - зависима.

Следствие: В n-мерном пространстве любая линейно – зависимая система может содержать не более n векторов.

Таким образом, на плоскости линейно – независимыми могут быть только два вектора. Любой третий вектор можно представить линейной комбинацией этих двух векторов. В 3-х мерном пространстве линейно - независимыми могут быть не более трёх векторов и т.д.

Начало формы

Пример : Является ли система векторов = (1;0;0); = (0;1;0) и = (0;0;1) линейно зависимой?

Решение: Составляем нулевую линейную комбинацию:

(1;0;0)λ₁ + (0;1;0)λ₂ + (0;0;1)λ₃ =(0;0;0)

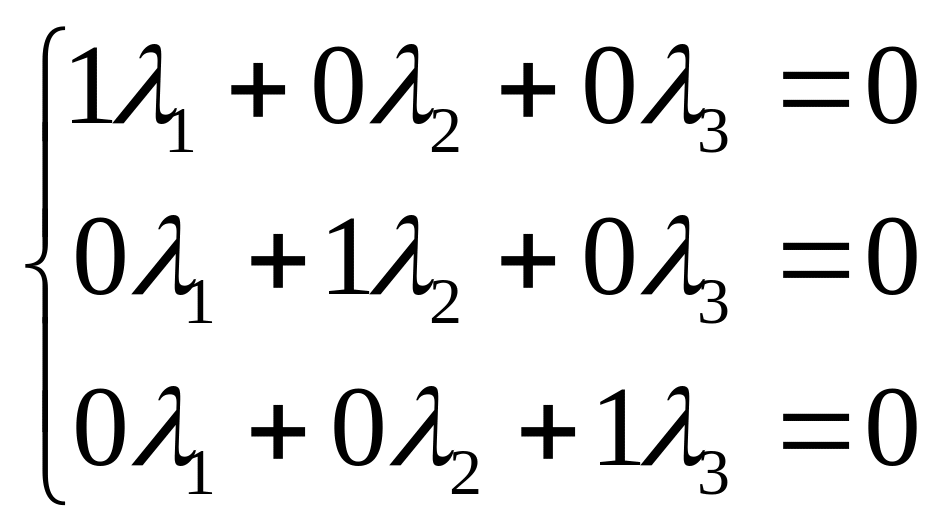или

Все значения , следовательно, система векторов – линейно – независима. Очевидно, что система из n n-мерных ортов является линейно-независимой.