6. Векторное произведение двух векторов

Пусть в пространстве зафиксирован ортонормированный базис R=={O,(i,j,k)}и пусть a,b- любые фиксированные вектора.

Определение.

Векторным произведением векторов a и b (обозначается [a,b] или ab) называется такой третий вектор с, который определяется следующими условиями:

1) модуль вектора с=аbsin( )

2) c перпендикулярен каждому из перемножаемых векторов са, сb,

3) тройка векторов (a,b,c) одинаково ориентирована с тройкой базисных векторов (i,j,k).

Свойства векторного произведения

1. Два вектора колинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

ab  [a,b]=

2. Модуль векторного произведения равен площади параллелограмма, построенного на векторах a и b (согласно определения).

[a,b]=S_пар.

3. Числовой множитель можно выносить за знак векторного произведения.

[a,b]= [a,b]=[a,b].

4. Векторное произведение двух векторов антикоммутативно, то есть если поменять местами сомножители, то векторное произведение изменит знак.

[a,b]= - [b,a].

5. Векторное произведение векторов дистрибутивно относительно суммы

[a+b,c]= [a,c] +[b,c].

Векторное произведение векторов в координатах

Пусть в пространстве задана декартовая прямоугольная система R=={O,(i,j,k)}и относительно этой системы заданы векторы a=(a₁,a₂,a₃), b=(b₁,b₂,b₃), тогда

[a,b]=

Площадь треугольника

Векторное произведение позволяет вместе со скалярным произведением решать метрические задачи в плоскости.

Пусть в пространстве зафиксирован R=={O,(i,j,k)} и дан треугольник М₁М₂М₃ с вершинами М₁(x₁,y₁,z₁), M₂ (x₂,y₂,z₂), М₃(x₃,y₃,z₃). Рассмотрим векторы М₁М₂ и М₁М₃, совпадающие со сторонами треугольника и построим на этих векторах параллелограмм.

S_треуг=1/2S_пар.=1/2[М₁М_2, М₁М₃] (1)

М₁М₂=( x_2- x₁, y_2- y_1, z_2- z₁)

М₁М₃=( x_2- x₁, y_2- y_1, z_2- z₁₎

[М₁М_2, М₁М₃]= (2)

(1),(2) S_треуг=

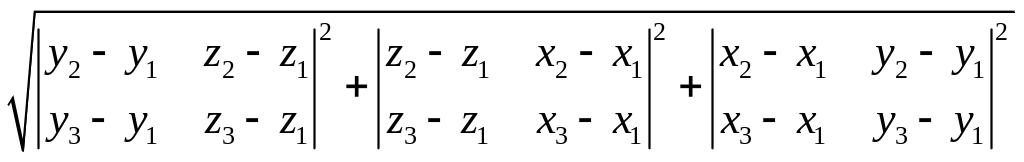
7. Смешанное произведение трёх векторов

Пусть в пространстве зафиксирован ортонормированный базис R=={O,(i,j,k)}и пусть a,b,с- любые фиксированные вектора.

Определение.

Смешанным произведением трёх векторов a,b,с называется число, равное скалярному произведению векторного произведения первых двух векторов на третий.

(a,b,c)=([a,b],c)=(a,[b,c]).

Теорема.

Абсолютная величина смешанного произведения трёх векторов равна объёму параллелепипеда построенного на этих векторах.

S_{параллелеп.}H=V

.

Свойства.

1. (a,b,c)=0 тогда и только тогда, когда {a,b,c}комплонарны.

2. Если поменять местами два соседних сомножителя, то смешанное произведение поменяет знак на противоположный.

(a,b,c)= -(b,c,a).

3.При круговой перестановке смешанное произведение не меняется.

(a,b,c)= (b,c,a)= (c,a,b)

(b,a,c)= (a,c,b)= (c,b,a).

4. Числовой множитель можно выносить за знак произведения.

(a,b,c)= (a,b,c).

5. Смешанное произведение векторов дистрибутивно

(a+b,c,d)= (a,c,d)+(b,c,d).

Вычисление смешанного произведения трёх векторов в координатах

Пусть в пространстве задана декартовая прямоугольная система R=={O,(i,j,k)}и относительно этой системы заданы векторы a=(a₁,a₂,a₃), b=(b₁,b₂,b₃), с=(с₁,с₂,с₃).

(a,b,c)=([a,b],c)

[a,b]=

с=(с₁,с₂,с₃).

(a,b,c)= .

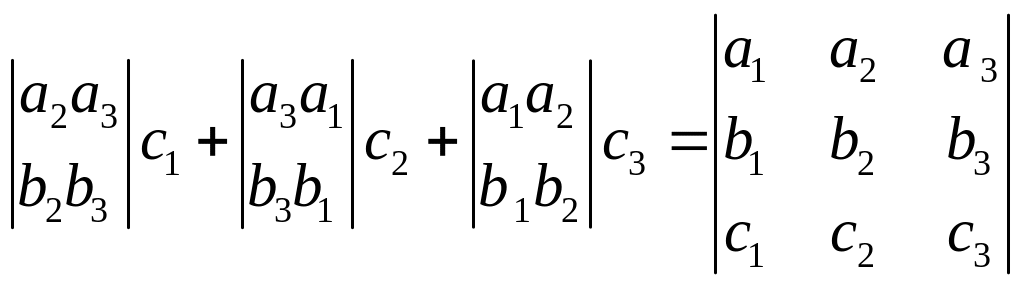То есть смешанное произведение это число, равное определителю, строки которого составлены из координатных строк векторов, входящих в смешанное произведение.

Непосредственно из свойств определителя третьего порядка следуют вышеперечисленные свойства.