1) Кинематика. Основные понятия. Система отсчета, материальная точка, траектория, путь и перемещение материальное точки. Скорость, средняя скорость. Ускорение, тангенсальное и нормальное ускорение. Принцип относительности Галлилея, переходы между различными Системами отсчета.

Кинема́тика — раздел механики, изучающий математическое описание (средствами геометрии, алгебры, математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.). Исходные понятия кинематики — пространство и время.

Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел.

Траекто́рия материа́льной то́чки  — линия в пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве.

Перемеще́ние — изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение.

Ско́рость — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта.

Средняя скорость это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:

Центростремительное ускорение — компонент ускорения точки, характеризующая изменение направления вектора скорости для траектории с кривизной. Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделенному на радиус кривизны. Термин «центростремительное ускорение» в целом эквивалентен термину «нормальное ускорение»; различия лишь стилистические .

Тангенциа́льное ускоре́ние  — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости в отличие от нормальной компоненты, характеризующей изменение направления скорости. Тангенциальное ускорение равно произведению единичного вектора, направленного по скорости движения, на производную модуля скорости по времени.

Принцип относительности - все уравнения механики запишутся одинаково в любой инерциальной системе отсчета — иначе говоря, законы механики не зависят от того, в какой из инерциальных систем отсчета мы их исследуем, не зависят от выбора в качестве рабочей какой-либо конкретной из инерциальных систем отсчета. Также — поэтому — не зависит от такого выбора системы отсчета наблюдаемое движение тел (учитывая, конечно, начальные скорости).

2) Законы движения. Зависимости координат от времени для равномерного и равноускоренного движения. Уравнения траектории (особо обратите внимание на движение тебя брошенного под углом к горизонту). Вращательное движение. Угловая скорость, период и частота обращения. Кинематические Связи (особо обратите внимание на качение без проскальзывания)

Движение с постоянным ускорением называют равноускоренным. Движение с постоянным ускорением подчиняется закону:

 ;

.

При этом уравнения движения в координатной форме имеют аналогичный вид:

 ;

.

Равноме́рное движе́ние — механическое движение, при котором тело за любые равные отрезки времени проходит одинаковое расстояние. Равномерное движение материальной точки — это движение, при котором скорость точки остаётся неизменной. Перемещение, пройденное точкой за время , задаётся в этом случае формулой .

Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной.

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

3) Заклны Ньютона. Инерциальные и неинерциальные системы отсчета. Силы в механике (сила упругости, сила трения)

1ый закон: Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.

2ой закон: В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:

 — ускорение материальной точки;  — сила, приложенная к материальной точке;  — масса материальной точки.

3закон: Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

Неинерциа́льная систе́ма отсчёта — система отсчёта, к которой не применим закон инерции (говорящий о том, что каждое тело, в отсутствие действующих на него сил, движется по прямой и с постоянной скоростью), и поэтому для согласования сил и ускорений в которой приходится вводить фиктивные силы инерции. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, является неинерциальной.

Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой справедлив первый закон Ньютона (закон инерции): все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерно или покоятся^[1]. Эквивалентной является следующая формулировка, удобная для использования в теоретической механике^[2]:

Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время — однородным.

Си́ла упру́гости — сила, возникающая при деформации тела и противодействующая этой деформации.

Закон Гука: В простейшем случае одномерных малых упругих деформаций формула для силы упругости имеет вид:

,

где  — жёсткость тела,  — величина деформации .

В словесной формулировке закон Гука звучит следующим образом:

Сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению тела и направлена противоположно направлению перемещения частиц тела относительно других частиц при деформации.

Сила трения - это сила, возникающая в месте соприкосновения тел и препятствующая их относительному движению

4) Закон всемирного тяготения. Законы Кеплера. Орбитальное движение. Первая космическая скорость.

(Зако́н всео́бщего тяготе́ния Ньюто́на) — закон, описывающий гравитационное взаимодействие в рамках классических рамках. Этот закон был открыт Ньютоном в 1666 году. Он гласит, что сила гравитационного притяжения между двумя материальными точками массы и , разделёнными расстоянием , пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:

Здесь  - гравитационная постоянная, равная м³/(кг с²).

Первый закон Кеплера (закон эллипсов)

Первый закон Кеплера.

Каждая планета Солнечной системы обращается по эллипсу,в одном из фокусов которого находится Солнце. Форма эллипса и степень его сходства с окружностью характеризуется отношением , где — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), -большая полуось. Величина называется эксцентритетом эллипса. При , и, следовательно, эллипс превращается в окружность.

Второй закон Кеплера (закон площадей)

Второй закон Кеплера.

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

Третий закон Кеплера (гармонический закон)

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.

, где и  — периоды обращения двух планет вокруг Солнца, а и  — длины больших полуосей их орбит.

Пе́рвая косми́ческая ско́рость — скорость, которую необходимо придать объекту, который после этого не будет использовать реактивное движение, чтобы вывести его на круговую орбиту (пренебрегая сопротивлением атмосферы и вращением планеты). Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.

5) Импульс материальной точки, импульс системы материальных точек, изменение импульса, импульс силы.

И́мпульс (Количество движения) – векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:

.

В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:

И́мпульс си́лы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени.

6) Замкнутые (изолированные) системы отсчета. Сохранение импульса системы материальных точек. (вывод)

Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.

Вывод из формализма Ньютона

Рассмотрим второй закон Ньютона

Перепишем его для системы из N частиц:

где суммирование идет по всем силам, действующим на n-ю частицу со стороны m-ой. Согласно третьему закону Ньютона, силы вида и будут равны по абсолютному значению и противоположны по направлению, то есть Тогда после подстановки полученного результата в выражение (1) правая часть будет равна нулю, то есть:

или

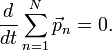
Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит:

(постоянный вектор).

То есть суммарный импульс системы частиц есть величина постоянная. Нетрудно получить аналогичное выражение для одной частицы.

Следует учесть, что вышеприведенные рассуждения справедливы лишь для замкнутой системы

Также стоит подчеркнуть, что изменение импульса зависит не только от действующей на тело силы, но и от продолжительности её действия.

7) Работа силы. Энергия. Полная механическая энергия системы материальных точек.(вывод)

Кинетическая энергия, потенциальная, потенциальная энергия упругого взаимодействия.

Эне́ргия — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется во времени. Это утверждение носит название закона сохранения энергии.

В физике механи́ческая эне́ргия описывает сумму потенциальной и кинетической энергии, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.

8) Сохранение Энергии. Теорема об изменении полной механической энергии.

Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени.

Теорема об изменении полной механической энергии.

ΔE = А , где ΔE – изменение полной механической энергии системы тел. А – работа внешних сил над системой и работа внутренних неконсервативных сил (типа силы трения).

9) Колебания. Гармонические колебания. Условия установления колебаний. Закон движения при гармонических колебаниях. Превращения энергии при колебаниях

Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.

Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

или

,

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд  — полная фаза колебаний,  — начальная фаза колебаний.

10) Механические гармонические колебания. Пружинный и математический маятники. Период колебаний. Зависимости скорости, ускорения и координаты от времени. Энергия колебаний.

Кинетическая энергия материальной точки, которая совершает прямолинейные гармонические колебания:

(3) или (4) (3) или (4) Потенциальная энергия материальной точки, которая совершает гармонические колебания под действием упругой силы F, будет равна (5) или (6) Сложив (3) и (5), найдем выражение для полной энергии: (7)

Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости k, один конец которой жёстко закреплён, а на втором находится груз массы m.

Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения.Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.

В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене. Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:

Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:

, где f(x) — это равнодействующая внешних сил соотнесённая к единице массы груза.

В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:

Математи́ческий ма́ятник – осциллятор представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения.Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен

и не зависит от амплитуды колебаний и массы маятника.

Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние, в котором он находился в первоначальный момент, выбранный произвольно).

При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W:

(Скорость тела v = ds/dt)

        Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы:

где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.

        Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем:

Сравнивая формулы

для кинетической и потенциальной энергии механического маятника, можно сделать следующие выводы:

1. Полная механическая энергия тела не изменяется при колебаниях: 2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника. 3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на  (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная - минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.

11) МКТ. Основные постулаты и явления их подтверждающие.

Молекулярно-кинетическая теория (сокращённо МКТ) — теория XIX века, рассматривавшая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений:

• все тела состоят из частиц: атомов, молекул и ионов

• частицы находятся в непрерывном хаотическом движении (тепловом);

• частицы взаимодействуют друг с другом путём абсолютно упругих столкновений.