8.Основные принципы определения объема выборки.

Выборка (выборочная сов-сть) – ограниченная группа респондентов, идентичная всему иссл-му множ-ву.

Генеральная сов-сть (изучаемая) – цел. аудит., на кот. распростр-ся выводы, сдел. при изуч. выборки.

След. сформир. такую выборку из генер. совок-ти, инф-я о кот. будет репрезентативной (представительной).

Объем выборки зависит от 2х факторов: стоимости сбора инф-ции и стремления к опред. степени статистич. достоверности результатов, кот. надеется получить иссл-тель. Чем больше размеры выборки (чем ближе они к размерам ген. сов-ти в целом), тем надежнее и достовернее получ. данные. ошибка выборки может зависеть не только от ее величины, но и от степени различий между отд. единицами внутри данной ген. сов-сти. Если, напр., нормы потребления продукта у разных людей сущ-венно различны, это гетерогенная ген. сов-сть, если они различаются меньше – гомогенная. Чем больше различия, тем больше возм. ошибка выборки. Объем выборки зав. от уровня однородности изуч. объектов: чем больше однородность, тем меньшая числ-сть может обеспечить статистически достоверные выводы.

Определение объема зав. также от уровня доверит. интервала допустимой стат. ошибки (случ. ошибки, связ. с природой любых стат.погрешностей).

Чем важнее решение, тем больше объем. На объем выборки может влиять хар-р исследования. Если это качеств. (поисковые) МИ, то на объем выборки это не влияет. А если это описат. МИ, то объем выборки больше.

Методы опред-я объема выборки:

1) произвольный метод – на уровне 5-10% от ген. совок-ти;

2) традицион. метод – провед-е периодич. иссл-й 500, 1000 или др. кол-ва респонд.;

3) статистический метод – опред-е статист. надежности информации;

5) эмпирический метод: выборка счит. достаточ., когда нов. сведения вносят незначит. измен-я (кот. можно пренебречь) в собран. рез-ты иссл-я;

6) затратный метод, основ-й на размере расх., кот. допустимы при пров. иссл-я.

9.Норм.Распределение. Правило 3х сигм.

Нормальное распределение используется для отражения социально-экономических явлений. Поэтому оно используется для обоснования параметров выборочной совокупности.

Практическое значение:

Если исследования простой случайной выборки, то можно определить ошибку при помощи Z – отклонений.

, где Z –стандартное распределение, оно отражает стандартное значение отклонения, µ - средняя генеральная совокупность, Xi – значение совокупности, σ – среднеквадратическое отклонение.

, где n – объем выборки, Z² – требуемый уровень надежности, σ² – дисперсия генеральной совокупности, H²– требуемый уровень точности.

Если данные представленные долевой средней, т.е. характеризуются %-ом долей, то

, где Р – доля признака, 1-р – доля объектов, не обладающих признаком, - долевое среднеквадратичное отклонение.

Определение объема выборки при использовании долей

, где р – доля существующего признака.

Интервал доверия//надежность позволяет с учетом точности определить выборочное значение.

Доверительный интервал -

Исп.в мат.статистике и практич.деят-ти. Если исп.случ.выборка, можно уст.ошибку, допустимую при помощи Z-отклонения.

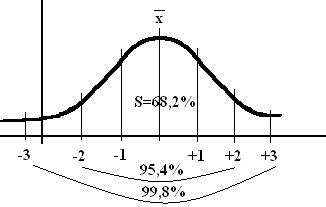
Правило трёх сигм — практически все значения нормально распределённой случайной величины лежат в интервале (-3;+3). Более строго — не менее чем с 99,7 % достоверностью, значение нормально распределенной случайной величины лежит в указанном интервале. При условии что величина истинная, а не полученная в результате обработки выборки.

Если же истинная величина неизвестна, то следует пользоваться не σ, а s. Таким образом, правило 3-х сигм преобразуется в правило трех s.

Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.

_{Пусть имеется нормально распределённая случайная величина  с математическим ожиданием, равным а и дисперсией 2. Определим веро­ятность попадания  в интервал (а – 3; а + 3), то есть вероятность того, что  принимает значения, отличающиеся от математического ожидания не более, чем на три среднеквадратических отклонения.}

_{P(а – 3<  < а + 3)=Ф(3) – Ф(–3)=2Ф(3)}

_{По таблице находим Ф(3)=0,49865, откуда следует, что 2Ф(3) практи­чески равняется единице. Таким образом, можно сделать важный вывод: нормальная случайная величина принимает значения, отклоняющиеся от ее математического ожидания не более чем на 3.}

_{(Выбор числа 3 здесь условен и никак не обосновывается: можно было выбрать 2,8, 2,9 или 3,2 и получить тот же вероятностный результат. Учитывая, что Ф(2)=0,477, можно было бы говорить и о правиле 2–х “сигм”.)}