Основное уравнение мкт в форме Клаузиуса.
P,V,T – параметры состояний, характеризующие термодинамическую систему.
Уравнение
Менделеева - Клаперона:
,
феноменологическое уравнение
Это уравнение описывает равновесное состояние термодинамической системы.
Равновесное состояние – такое состояние, при котором все параметры системы остаются постоянными
Принцип локального равновесия – позволяет рассчитывать локальные состояния по уравнению равновесного состояния
Вывод уравнения:
Будем считать, что взаимодействия со стенкой упругое и применим для описания этого взаимодействия закон Ньютона.
=>
ν – частота
соударений
=>
=>
=>
– основное уравнение МКТ в форме
Клаузиуса.
Связывает V и P c энергией движения молекул
Связь скорости теплового движения молекул с температурой. Уравнение Больцмана.
Распределение энергии по степеням свободы молекул. Понятие температуры в МКТ.
,
где <ε>
- среднее значение кинетической энергии
молекулы
k – постоянная Больцмана
Уравнение Больцмана:
Запишем
уравнение
.
Это формула определяет только энергию
поступательного движения.
Но наряду с поступательным движением возможны также вращение молекул и колебания атомов в молекуле.
Т.к. оба эти движения тоже связаны с некоторым запасом энергии, определить общую энергию позволяет положение о равнораспределении энергии по степеням свободы молекулы.
Числом степеней свободы механической системы называют количество независимых величии, с помощью которых может быть задано положение системы. Степени свободы бывают поступательные, вращательные, колебательные). Рассматривает атомы как материальные точки, молекулы с жесткой связью атомов.
Например, для одноатомной молекулы, число степеней свободы(i) равно 3.
Для двухатомной молекулы – 5(3 поступательных, 2 вращательных(2 оси вращения, третья бессмысленна))
Для многоатомной молекулы – 6(3 поступательных, 3 вращательных(3оси вращения))
Для
любой молекулы обязательны 3 поступательных
степени свободы. Т.к. ни одна из них не
имеет преимущества перед остальными,
на каждую из них приходится по формуле
энергия равная
.
В классической статической физике выводится закон равнораспределения, согласно которому на каждую степень свободы приходится в среднем одинаковая кинетическая энергия равная .
Таким
образом, средняя энергия молекулы должны
равняться:
.(Уравнение
МКТ в форме Больцмана).
Понятие температуры в МКТ
К определению понятия температуры можно прийти на основании следующих соображений. Если соприкасающиеся тела находятся в состоянии теплового равновесия, т.е. не обмениваются энергией путем теплопередачи, то этим телам приписывается одинаковая температура.
Если при установлении теплового контакта между телами одно из них передает энергию другому посредством теплопередачи, то первому приписывается большая температура, чем второму.
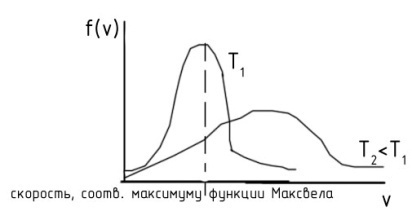
Распределение молекул по скоростям их движения (распределение Максвелла).
Максвелл предположил, что скорость частиц газа подчиняется закону Гаусса.
Из условий:
- компоненты скорости независимы
- подчиняются закону Гаусса
- вероятности умножаются
выведем:
