6) Момент импульса. Закон сохранения момента импульса.

Момент импульса – векторное произведение радиус-вектора на импульс точки

, где L - момент импульса

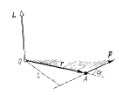
С помощью момента импульса рассчитывают вращательное движение

Свойства

1. - аксиальный вектор, его направление определяется правилом правой руки

2. – аддитивный вектор

3. Зависит от положения точки отсчета и ,соответственно, системы отсчета

Если продифференцируем по времени:

- момент силы

Для системы материальных точек:

;

, если , то L – const – закон сохранения момента импульса.

Момент импульса в замкнутой системе остается постоянным, т.е не меняется со временем

Фундаментальный закон .является следствием изотропности пространства.

7. Закон изменения момента импульса. Момент силы. Момент инерции тела (пример расчета).

продифференцируем по времени:

- момент силы

Для системы материальных точек:

;

, если , то – закон изменения момента импульса

Момент силы – вектор.

Свойства:

1. аксиальный

2. аддитивный

3. зависит от выбора СО

Момент инерции:

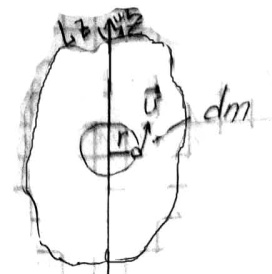
, где I - момент инерции материальной точки

,где

Свойства момента инерции:

1. аддитивная величина

2. скалярная величина

3. зависит от выбора оси

4. зависит от конфигурации(формы) тела

Характеризует инерционные свойства тела при вращательном движении

;

– уравнение движения вращающегося тела(второй закон Ньютона)( подобна формуле: ma=∑F)

Примеры вычисления момента инерции:

1. - формула для вычисления момента инерции обруча, точки, тонкого цилиндра вокруг оси

2. Для вычисления момента инерции плоского диска относительно оси, совпадающей с геометрической осью

П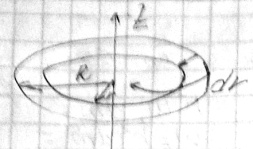 усть R – радиус диска, r – радиус обруча, М - масса диска

; →

3. в

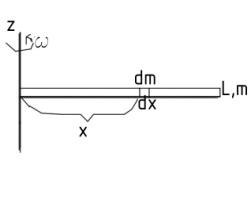
Момент инерции тонкого длинного стержня

Ось вращения проходит через конец стержня

,

Ось вращения проходит через середину стержня

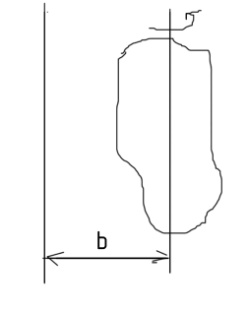
Теорема Штейнера

Момент инерции I относительно произвольной оси z равен моменту инерции I0 относительно оси z0, параллельной данной и проходящей через центр масс тела плюс произведение массы m тела на квадрат расстояния b между осями

7. Работа, мощность. Работа консервативных и неконсервативных сил.

Работа силы:

Работа - скалярная величина

Cилы:

1. консервативные – силы, работа которых не зависит от пути(траектории, формы), а зависит только от начального и конечного положений

Консервативные силы являются потенциальными.

Консервативные силы: силы упругости, сила Архимеда, силы инерции

2. Неконсервативные силы – работа зависит от формы траектории

Неконсервативные силы: сила сопротивления среды

Неконсервативные силы являются непотенциальными, диссипативными

Мощность – скорость, с которой совершается работа; работа, совершаемая силой за единицу времени.

Мощность – алгебраическая величина

Единица мощности – ватт=Дж/с

7. Потенциальная энергия. Связь силы и потенциальной энергии.

Потенциальная энергия – потенциальная возможность совершения какого-либо количества работы

Свойства потенциальной энергии:

1. скалярная величина

2. алгебраическая величина

3. определяется с точностью до произвольной постоянной величины(неопределенной)

4. в общем случае неаддитивная

;

Пример:

=>

при r₀→∞:

Сила притяжения всегда имеет отрицательную потенциальную энергию.

Связь силы и потенциальной энергии

перемножим скалярно на =>

=> ;

grad – вектор, который показывает направление максимальной скорости изменения той функции, к которой он применяется.

Знак “–“ показывает, что сила направлена в сторону убывания