Операции над векторами:

1. Сложение

Суммой a + b векторов a и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а.

2. Вычитание

Разностью а – b векторов а и b называется такой вектор с, который в сумме с вектором b дает вектор а.

3. Произведение

Произведением ka вектора а на число k называется вектор b, коллинеарный вектору а, имеющий модуль, равный |k||a|, и направление, совпадающее с направлением а при k>0 и противоположное а при k<0.

 

Свойства умножения вектора на число:

Свойство 1. k(a + b) = ka + kb.

Свойство 2. (k + m)a = ka + ma.

Свойство 3. k(ma) = (km)a.

Длиной или модулем ненулевого вектора  называется длина отрезка . Длина нулевого вектора  равна нулю.

Единичный вектор, направленный вдоль оси Х, обозначается i, единичный вектор, направленный вдоль оси Y , обозначается j, а единичный вектор, направленный вдоль оси Z, обозначается k. Векторы i, j, k называются ортами, они имеют единичные модули, то есть i = 1, j = 1, k = 1.

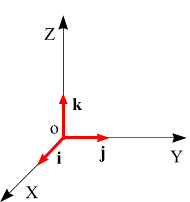
Проекция вектора на ось.

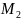
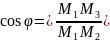
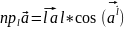, 0≤ ≤π

Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат.

Направление вектора однозначно задается направляющими косинусами. Для единичного вектора направляющие косинусы равны его координатам.

Если в пространстве задан вектор , то его направляющие косинусы вычисляются по формулам:

Здесь, и - углы, которые составляет вектор с положительными направлениями осей , и соответственно.

Основное свойство направляющих косинусов:

Сумма квадратов направляющих косинусов равна единице.

Если известны направляющие косинусы вектора , то его координаты могут быть найдены по формулам:

Аналогичные формулы имеют место и в трехмерном случае - если известны направляющие косинусы вектора , то его координаты могут быть найдены по формулам: