1. Понятие матрицы. Транспонирование матрицы. Равенство матриц. Виды матриц.

Матрица- прямоугольная таблица чисел или функции, содержащая m-строк и n-столбцов одинаковой длины.

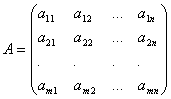
Матрица, полученная из данной матрицы А заменой каждой ее строки столбцом с тем же номером называется матрицей, транспонированной к данной.

Две матрицы равны когда они одного размера и все их элементы совпадают. Есл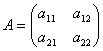и

и , то A=B, если a₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁ и a₂₂ = b₂₂.

Виды матриц:

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной.

Если в матрице число строк равно числу столбцов, то матрица называется квадратной.

Диагональная матрица — квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.

или

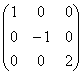
Диагональная матрица, у которой каждый элемент главной диагонали равен 1, называется единичной.

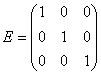
Квадратная матрица называется треугольной, если все элементы, лежащие ниже главной диагонали равны 0.

Матрица, все элементы которой равны 0, называется нулевой.

2. Понятие матрицы. Виды матриц. Линейные операции над матрицами и их свойства.

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу

Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:

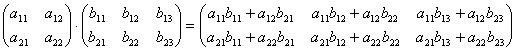
Свойства:

1. А+В=В+А

2. А+(В+С)=(А+В)+С

3. А+0=А

4. А=А

5. А-А=0

6. α(А+В)=αΑ+αВ

7. (α+β)*А=

8. α(Аβ)=(αβ)А

9. А(ВС)=(АВ)С

10. А(В+С)=АВ+АС

11. (А+В)С=АС+ВС

12. (αβ)А=α(ВА)

13. = +

14. 

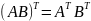
15. АВ≠ВА (в общем случае) при согласованности матриц

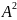16. =АА

3. Определители второго и третьего порядков. Формулы для их вычисления и свойства. Миноры, алгебраические дополнения. Основное свойство (теорема Лапласа) о разложении определителя по элементам строки или столбца.

Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом: a₁₁a₂₂ – a₁₂a₂₁.

Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:

Свойства определителей:

1. при транспонировании матрицы определитель сохраняется

2. при перестановке 2 параллельных рядом определитель меняет знак.

3. Определитель, имеющий 2 одинаковых ряда, равен 0.

4. Общий множитель элементов какого-то ряда можно вынести за знак определителя.

5. Если элементы какого-то ряда определителя представляют собой сумму 2 слагаемых, то определитель может быть разложен на сумму 2 соответствующих определителей.

6. Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.

7. Определитель треугольной матрицы равен произведению элементов главной диагонали.

Минор k -го порядка матрицы – определитель матрицы, составленный из элементов данной матрицы, стоящих на пересечении произвольно выделенных ее k строк и k столбцов с сохранением их порядка, т.е. минор k-го порядка есть определитель квадратной матрицы размера k x k.

Каждая n x m матрица имеет миноров k-го порядка. Минорами 1-го порядка являются элементы матрицы. Если номера строк, в которых расположен минор, совпадают с номерами столбцов, то он называется главным минором.

Базисный минор матрицы – отличный от нуля минор k-го порядка этой матрицы такой, что все содержащие его миноры (k+1)-го порядка равны нулю, или же минор (k+1)-го порядка не существует. Порядок любого базисного минора матрицы совпадает с рангом матрицы, причем каждый столбец (строка) матрицы есть линейная комбинация линейно независимых столбцов (строк), в которых расположен базисный минор.

В квадратной матрице n-го порядка дополнительным минором к минору k-го порядка называется определитель (n-k)-го порядка, полученный из данной матрицы вычеркиванием тех k столбцов и строк, в которых расположен минор k-го порядка.

Алгебраическим дополнением минора матрицы называется  его дополнительный минор, умноженный на (-1) в степени, равной сумме номеров строк и номеров столбцов минора матрицы.

 В частном случае, алгебраическим дополнением элемента матрицы называется его дополнительный минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.

Теорема Лапласса: Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

4. Квадратная матрица n-го порядка и ее определитель. Вырожденная и невырожденная квадратная матрицы. Миноры, алгебраические дополнения. Присоединенная (союзная) матрица.

Матрица называется вырожденной, если ее определитель равен нулю, и невырожденной, если определитель матрицы отличен от нуля.

Союзная матрица — это матрица, элементы которых являются алгебраическими дополнениями, соответствующих элементов исходной матрицы.

5. Присоединенная (союзная) матрица. Матрица, обратная данной. Алгоритм и формула вычисления обратной матрицы. Матричные уравнения AX=B, XA=B (вывод решения).

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует.

Формула:

Алгоритм:

1. Сначала находим определитель матрицы.

Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.

2. Находим матрицу миноров .

3. Находим матрицу алгебраических дополнений .

4. Находим транспонированную матрицу алгебраических дополнений .

5. Ответ.

Матричные уравнения:

AX=B ХА=В

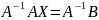
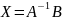Х=В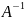

6. Элементарные преобразования строк матрицы. Понятие ступенчатой матрицы. Ранг матрицы. Вычисление ранга матрицы с помощью элементарных преобразований. (на примере 4 из т.р 1). Теорема о ранге матрицы.

Элементарные преобразования матриц:

1) Перестановка местами параллельных строк (столбцов) матриц.

2) Нулевой ряд вычеркиваем.

3)Умножение "ряда" на нулевое число.

4) Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Матрица называется ступенчатой, если выполнены следующие условия:

• после нулевой строки идут только нулевые строки.

• опорный элемент в каждой последующей строке расположен правее, чем предыдущий.

Пример ступенчатой матрицы:

Ранг матрицы -число ненулевых строк в ее ступенчатом виде.

Пример. Найти ранг матрицы:

Решение. Приведем матрицу А к ступенчатому виду.

Теорема о ранге матрицы.

Строчный и столбцовый ранги матрицы А  совпадают.

7. Система m линейных уравнений с n переменными (общий вид). Матричная форма записи такой системы. Определение решения системы. Совместные и несовместные, определенные и неопределенные системы линейных уравнений.

Система m линейных уравнений с n переменными имеет вид:

или

где

-произвольные числа, называемые соответственно коэффициентами при переменных и - свободными членами уравнений.

Решением системы (1) называется такая совокупность n чисел ,

при подстановке которых каждое уравнение системы обращается в верное равенство.

Решить систему, значит выяснить совместна она или нет.

Система линейных уравнений называется совместной, если она имеет хотя бы одно решение.

Система линейных уравнений называется несовместной, если она не имеет ни одного решения.

Совместная система линейных уравнений называется определенной, если она имеет единственное решение.

Совместная система линейных уравнений называется неопределенной, если она имеет много решений.

8. Решение систем n линейных уравнений с n переменными с помощью обратной матрицы. (вывод формулы для Х из матричного уравнения АХ=В) (на примере 3 а из т.р.1)

Пусть число уравнений системы равно числу переменных, т.е. m=n. Тогда матрица системы является квадратной, а ее определитель называется определителем системы.

Уравнение можно записать в матричном виде

А*Х=B

Умножая слева обе части матричного равенства на матрицу ,получим . Так как , то решением системы методом обратной матрицы будет матрица-столбец:

.

9. Теорема Крамера (формула Крамера) решения системы n линейных уравнений с n переменными. (на примере 3 б из т.р. 1)

Теорема Крамера. Пусть |A|— определитель матрицы системы А, а — определитель матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов. Тогда, если , то система имеет единственное решение, определяемое по формулам:

10. Метод Гаусса решения системы m линейных уравнений с n переменными. (на примере 4 из т.р. 1)

Метод Гаусса — метод последовательного исключения переменных — заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Рассмотрим решение системы m линейных уравнений с n переменными в общем виде:

Если m=n, то рассмотрим расширенную матрицу. Учитывая правую часть, приведем данную матрицу к треугольному виду:

Система линейных уравнении соответствующее данной матрице запишем в следующем виде:

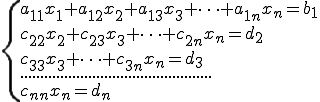
Если в данном уравнении то, в первую очередь найдем , а затем, постепенно поднимаясь, находим остальные решения -

.