13 Вопрос

Закон смещения Вина

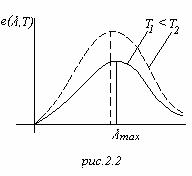температура входит в выражение для испускательной способности лишь в виде отношения .. Уже это обстоятельство позволяет предвидеть некоторые особенности интересующей нас функции. Тщательные измерения ряда исследователей привели к установлению эмпирического хода функции - и позволили проверить теоретические выводы Вина.

Кривые, полученные в результате этих исследований, приведены на рис. 1.9. Они выражают в функции . Из рисунка видно, что - для каждой температуры обладает максимумом. Для определения положения этого максимума в шкале А, перейдем в выражении закона Вина (7.1) от к , пользуясь соотношением :

.

Приравняв нулю производную , нетрудно видеть, что положение максимума удовлетворяет условию

,                                                                    (7.2)

 

Рис. 1.9.  Кривые распределения энергии в спектре черного тела для разных температур.

 

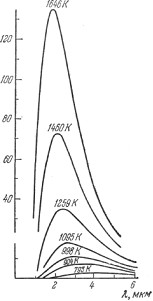
Метод исследования состоял в изучении распределения энергии по спектру излучения, посылаемого абсолютно черным телом различной температуры. Схема опытов приведена на рис. 1.8. Здесь S— абсолютно черное тело заданной температуры, L — линза, концентрирующая излучение на щели

где b не зависит от температуры. Приведенные на рис. 1.9 экспериментальные кривые подтверждают это заключение и дают возможность определить b.

Современное значение

В указанной форме закон Вина носит название закона смещения, ибо он показывает, что положение максимума функции по мере возрастания температуры смещается в область коротких волн.

В соответствии со сказанным выше можно решить задачу о положении максимума на кривой спектрального распределения в координатах , т. е. соответствующего формуле (7.1) Определяя положение максимума этой функции из условия =0, найдем, что оно соответствует соотношению

        ,

где а не зависит от Т и согласно измерениям а = 0,5100 см*град.

14 Вопрос

Формула Рэлея-Джинса

Закон Рэлея-Джинса — закон излучения Рэлея-Джинса для равновесной плотности излучения абсолютно чёрного тела u(ω,T) и для испускательной способности абсолютно чёрного тела f(ω,T) который получили Рэлей и Джинс, в рамках классической статистики (теорема о равнораспределении энергии по степеням свободы и представление об электромагнитном поле как о бесконечномерной динамической системе).

Правильно описывал низкочастотную часть спектра, при средних частотах приводил к резкому расхождению с экспериментом, а при высоких — к абсурдному результату (см. ниже), означавшему неудовлетворительность классической физики.

Вывод формулы

(график в координатах f(ω,T) от λ)

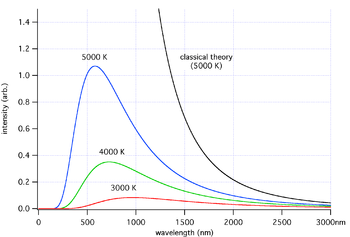
Зависимость испускательной способности абсолютно черного тела от длины волны для разных температур (выделены цветом) и её вид, исходя из классических рассуждений Релея и Джинса (черный цвет)

Основываясь на законе о равнораспределении энергии по степеням свободы: на каждое электромагнитное колебание приходится в среднем энергия, складываемая из двух частей kT. Одну половинку вносит электрическая составляющая волны, а вторую  —— магнитная. Само по себе, равновесное излучение в полости, можно представить как систему стоячих волн. Количество стоячих волн в трехмерном пространстве дается выражением:

.

В нашем случае скорость v следует положить равной c, более того, в одном направлении могут двигаться две электромагнитные волны с одной частотой, но со взаимно перпендикулярными поляризациями, тогда (1) в добавок следует помножить на два:

.

Итак, Релей и Джинс, каждому колебанию приписали энергию . Помножив (2) на ,получим плотность энергии, которая приходится на интервал частот dω:

,

тогда:

.

Зная связь испускательной способности абсолютно черного тела f(ω,T) с равновесной плотностью энергией теплового излучения , для f(ω,T) находим:

Выражения (3) и (4), называют формулой Релея-Джинса.

Формулы (3) и (4) удовлетворительно согласуются с экспериментальными данными лишь для больших длин волн, на более коротких волнах согласие с экспериментом резко расходится. Более того, интегрирование (3) по ω в пределах от 0 до для равновесной плотности энергии u(T) дает бесконечно большое значение. Этот результат, получивший название ультрафиолетовой катастрофы, очевидно, входит в противоречие с экспериментом: равновесие между излучением и излучающим телом должно устанавливаться при конечных значениях u(T). Однако ошибки в выводе формулы Релея-Джинса с классической точки зрения  —— нет. Очевидно несогласие с экспериментом вызвано некими закономерностями, которые несовместимы с классической физикой. Эти закономерности были определены Максом Планком: в 1900 году ему удалось найти вид функции u(ω,T), соответствующий опытным данным, в дальнейшем называемую формулой Планка.