44 Колебательно-вращательный спектр

Колебательно-вращательный спектр называют также ин фракрасным: спектром. Разрешающая способность обычного спектрального прибора слишком мала для разделения. При повышении давления или при конденсировании фаз эти линии исчезают, так как продолжительность существования отдельного вращательного состояния настолько сильно изменяется лри соударениях молекул, что наблюдается уширение и перекрывание линий. Спектры в ближней инфракрасной области i ( i от 1000 до 50 000 нм) обусловлены колебаниями атомов. Колебания возникают, если поглощение электромагнитного излучения связано с изменением направления и величины дипольного момента молекул. Поэтому молекулы, состоящие, например, из двух атомов, не могут давать инфракрасные спектры. Схема вращательного спектра комбинационного рассеяния молекулы типа симметричного волчка. Линии ветви S, накладывающиеся на линии ветви R, на рисунке. Колебательно-вращательные спектры возникают при перехода. Интенсивность колебательно-вращательных спектров испускания мала, они исследуются очень редко, практически исследуются спектры поглощения и спектры комбинационного рассеяния. В этом наиболее частом случае в спектре поглощения наблюдаются переходы только с основного колебательного уровня, а в спектре комбинационного рассеяния интенсивны только стоксовы полосы, также соответствующие переходам с основного колебательного уровня. Колебательно-вращательные спектры ( инфракрасные и комбинационного рассеяния) двухатомных молекул. Колебательно-вращательные спектры охватывают не только многоатомные молекулы с постоянным дипольным моментом. Колебательные спектры с низким разрешением присутствуют в инфракрасной области и области рамановских частот. Правила отбора, определяющие число линий рамановских и инфракрасных спектров, очень сильно зависят от симметрии. Так, например, линейная трехатомная молекула ВАВ обладает двумя сильными линиями в инфракрасном спектре и только одной сильной линией ( иной частоты) в раман-спектре. Оба спектра дополняют друг друга. Схема вращательного спектра комбинационного рассеяния двухатомной молекулы. Колебательно-вращательные спектры испускания редко исследуются из-за малой интенсивности.

Билет 45. Комбинационное рассеяние света

Комбинационное рассеяние света, рассеяние света веществом, сопровождающееся заметным изменением частоты рассеиваемого света. Если источник испускает линейчатый спектр, то при К. р. с. в спектре рассеянного света обнаруживаются дополнительные линии, число и расположение которых тесно связаны с молекулярным строением вещества. К. р. с. открыто в 1928 советскими физиками Г. С. Ландсбергом и Л. И. Мандельштамом при исследовании рассеяния света в кристаллах и одновременно индийскими физиками Ч. В. Раманом и К. С. Кришнаном при исследовании рассеяния света в жидкостях (в зарубежной литературе К. р. с. часто называют эффектом Рамана). При К. р. с. преобразование первичного светового потока сопровождается обычно переходом рассеивающих молекул на другие колебательные и вращательные уровни (см. Молекулярные спектры), причём частоты новых линий в спектре рассеяния являются комбинациями частоты падающего света и частот колебательных и вращательных переходов рассеивающих молекул — отсюда и назв. «К. р. с.».

Для наблюдения спектров К. р. с. необходимо сконцентрировать интенсивный пучок света на изучаемом объекте. В качестве источника возбуждающего света чаще всего применяют ртутную лампу, а с 60-х гг. — лазерный луч. Рассеянный свет фокусируется и попадает в спектрограф, где спектр К. р. с. регистрируется фотографическим или фотоэлектрическим методами.

К. р. с. наиболее часто связано с изменением колебательных состояний молекул. Такой спектр К. р. с. состоит из системы спутников, расположенных симметрично относительно возбуждающей линии с частотой n. Каждому спутнику с частотой n — ni (красный, или стоксов, спутник) соответствует спутник с частотой n + ni (фиолетовый, или антистоксов, спутник). Здесь ni— одна из собственных частот колебаний молекулы. Таким образом, измеряя частоты линий К. р. с., можно определять частоты собственных (или нормальных) колебаний молекулы, проявляющихся в спектре К. р. с. Аналогичные закономерности имеют место и для вращательного спектра К. р. с. В этом случае частоты линий определяются вращательными переходами молекул. В простейшем случае вращательный спектр К. р. с. — последовательность почти равноотстоящих симметрично расположенных линий, частоты которых являются комбинациями вращательных частот молекул и частоты возбуждающего света.

Согласно квантовой теории, процесс К. р. с. состоит из двух связанных между собой актов — поглощения первичного фотона с энергией hn (h — Планка постоянная) и испускания фотона с энергией hn' (где n' = n ± ni), происходящих в результате взаимодействия электронов молекулы с полем падающей световой волны. Молекула, находящаяся в невозбуждённом состоянии, под действием кванта с энергией hn через промежуточное электронное состояние, испуская квант h (n — ni), переходит в состояние с колебательной энергией hni. Этот процесс приводит к появлению в рассеянном свете стоксовой линии с частотой n — ni (). Если фотон поглощается системой, в которой уже возбуждены колебания, то после рассеяния она может перейти в нулевое состояние; при этом энергия рассеянного фотона превышает энергию поглощённого. Этот процесс приводит к появлению антистоксовой линии с частотой n + ni ().

Билет 46. Вынужденное излучение

Представление о квантовых энергетических уровнях атомов было введено в физику Н.Бором в 1913 г. Оно очень естественно объяснило линейчатые атомные спектры как результат процессов спонтанного (самопроизвольного) и з л у ч е н и я и резонансного (избирательного) п о г л о щ е н и я света атомами .

В 1919 г. Эйнштейн показал, что наряду с процессами спонтанного излучения и резонансного поглощения существует третий процесс — вынужденное (индуцированное) излучение. По Эйнштейну свет резонансной частоты, т. е. той частоты, которую атомы способны поглощать, переходя на более высокий квантовый уровень, должен вызывать высвечивание атомов, уже находящихся на этом верхнем уровне.

Характерная особенность вынужденного излучения состоит в том, что

испускаемый свет не отличим от вынуждающего света, т.е. совпадает с ним по всем признакам:по частоте, фазе, поляризации и направлению распространения.

Это означает, что вынужденное излучение добавляет в световой пучок точно такие же кванты, какие уводит из него резонансное поглощение. Поэтому на опыте проявляется только разность поглощения и вынужденного излучения.

Поглощают свет атомы, находящиеся на нижнем из двух участвующих в игре уровней, излучают же атомы, находящиеся на верхнем уровне. Ввиду этого, если среда содержит на нижнем уровне больше атомов, чем на верхнем, то преобладает поглощение н световой пучок ослабляется средой.

Напротив, если больше населен верхний уровень, то преобладает вынужденное излучение и среда усиливает проходящий свет. В последние годы это явление получило применение в очень перспективных приборах — квантовых усилителях и генераторах света.

Билет 47. Первый лазер (1960)

1960 год: Теодор Мейман продемонстрировал работу первого оптического квантового генератора — лазера[7]. В качестве активной среды использовался рубин (оксид алюминия Al2O3 с небольшой примесью хрома Cr), а вместо объёмного резонатора был использован открытый оптический резонатор. Этот лазер работал в импульсном режиме на длине волны в 694,3 нм[3]. В декабре того же года был создан гелий-неоновый лазер, излучающий в непрерывном режиме (А. Джаван, У. Беннет, Д. Хэрриот). Изначально лазер работал в инфракрасном диапазоне, затем был модифицирован для излучения видимого красного света[6].

Билет 48.Теплоемкость кристаллов

Модель Эйнштейна. В модели Эйнштейна считают, что атомы колеблются независимо друг от друга и что частоты колебаний всех атомов одинаковы. В таком случае для подсчета внутренней энергии кристалла, содержащего атомов, достаточно рассмотреть один осциллятор, а затем домножить результат на - число осцилляторов. Пусть каждый осциллятор имеет частоту . Средняя энергия, запасенная в таком осцилляторе, вычисляется с использованием распределения Бозе-Эйнштейна:

где - среднее число квантов энергии, "запасенных" в осцилляторе.

Энергия кристалла, содержащего атомов, тогда вычисляется как , а теплоемкость при постоянном объеме - дифференцированием энергии по температуре:

Модель дает хорошее совпадение с экспериментом для температур выше 50-100 К (не слишком близких к абсолютному нулю). График зависимости приведен на рис. 3.10.

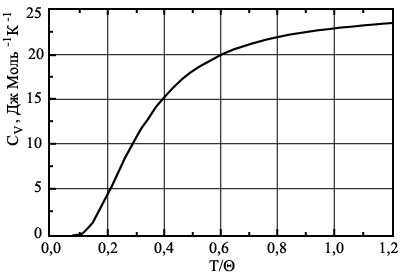При (случай высоких температур) , что соответствует известному закону Дюлонга и Пти. При (случай низких температур) при , как этого требует третье начало термодинамики. Однако, убывание оказывается более быстрым, чем наблюдают экспериментально . Это связано с некорректностью допущений о независимости колебаний отдельных атомов. Известно, что атомы взаимодействуют друг с другом, например ( раздел 3.2), в кристалле существуют упругие волны с разной длиной волны, соответствующие коллективным, зависящим друг от друга, колебаниям атомов

Билет 49. Закон Дюлонга – Пти

Закон Дюлонга-Пти - закон, согласно которому произведение удельной теплоемкости и относительной атомной массы для всех простых твердых тел приблизительно равно 25 (при условии, что удельная теплоемкость выражена в Дж. моль-1К-1).

Закон Дюлонга и Пти соблюдается для твердых одноатомных тел при достаточно высоких температурах. Для большинства тел такой достаточно высокой температурой является уже комнатная температура. Однако для некоторых тел с малой атомной массой, например для бериллия, бора, углерода (алмаза), комнатная температура недостаточно высока, и они подчиняются закону Дюлонга и Пти лишь при более высокой температуре. Наоборот, при охлаждении все тела обнаруживают отступления от закона Дюлонга и Пти. При охлаждении теплоемкость всех тел уменьшается.

Билет 50. Формула ДеБая

ЛАНЖЕВЕНА — ДЕБАЯ ФОРМУЛА, связывает диэлектрическую проницаемость e полярных диэлектриков с дипольным моментом р составляющих его молекул. Л.— Д. ф. имеет вид:

где Т — абс. темп-pa, М — молекулярная масса, r — плотность в-ва, a0—

электронная поляризуемость молекул, NA —Авогадро постоянная. Л,— Д. ф.— обобщение Клаузиуса — Моссотти формулы на случай полярного диэлектрика. Электрич. поле E вызывает преимуществ. ориентацию дипольных моментов молекул вдоль поля, чему препятствует тепловое движение. Вычисление проекции постоянного дипольного момента молекулы на направление E позволяет определить т. н. ориентац. поляризуемость молекул, приближённо равную р^2/3kT. Учёт ориентац. поляризуемости приводит к Л.- Д. ф.

Л.— Д. ф. была получена в 1912 П. Дебаем (P. Debye), который применил к полярным диэлектрикам формулу франц. физика П. Ланжевена (P. Langevin), полученную в 1905 при расчёте намагниченности парамагн. газов. Л.— Д. ф. применяется для определения дипольных моментов молекул по зависимости левой части (1) от Т-1. Область применения Л.— Д. ф. ограничена газами и парами из полярных молекул, разбавленными растворами полярных жидкостей в неполярных растворителях. Ф-ла (1) приближённо справедлива при условии рЕ<<kT, т.е. для относительно слабых полей и не очень низких темп-р.

Билет 51.Статистика Ферми Дирака

Статистика Ферми — Дирака в статистической физике — квантовая статистика, применяемая к системам тождественных фермионов (как правило, частиц с полуцелым спином, подчиняющихся принципу запрета Паули, то есть, одно и то же квантовое состояние может занимать не более одной частицы); определяет статистическое распределение фермионов по энергетическим уровням системы, находящейся в термодинамическом равновесии; предложена в 1926 г. итальянским физиком Энрико Ферми и одновременно английским физиком Полем Дираком, который выяснил её квантово-механический смысл; позволяет найти вероятность, с которой фермион занимает данный энергетический уровень.

Работы по статистике Ферми — Дирака были опубликованы в 1926, а в 1927 она была применена Арнольдом Зоммерфельдом к электронам в металле.

В статистике Ферми — Дирака среднее число частиц в состоянии с энергией есть

где:

• — среднее число частиц в состоянии i,

• — энергия состояния i,

• — кратность вырождения состояния i (число состояний с энергией ),

• — химический потенциал (который равен энергии Ферми 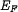при абсолютном нуле температуры),

k — постоянная Больцмана,

T — абсолютная температура.

В (идеальном) ферми-газе в пределе низких температур . В этом случае (полагая уровни энергии невырожденными ), функция распределения частиц называется функцией Ферми:

Билет 52. Распределение Бозе Эйнштейна

В классической физике распределение частиц по энергиям описывается хорошо известными из курса молекулярной физики распределением Максвелла

и распределением Больцмана

Здесь и - соответственно кинетическая и потенциальная энергии частицы, T- температура, k- постоянная Больцмана, и - нормировочные константы.

Распределение Бозе Эйнштейна:

Оно описывает распределение бозе-частиц по энергиям и определяет среднее число бозе-частиц , находящихся в квантовом состоянии с энергией . Величину называют также числом заполнения энергетического уровня с энергией .

Проанализируем следствия, вытекающие из вида распределения Бозе-Эйнштейна. Как следует из (6.39) , число бозе-частиц, находящихся на одном энергетическом уровне ( в одном состоянии ), ничем не ограничено и при малых значениях параметра может оказаться очень большим. Это важная отличительная особенность бозе-частиц.

Распределение Бозе-Эйнштейна используется для описания свойств систем, состоящих из бозе-частиц: как простых, например, фотонов, фононов, так и более сложных, составных, например, атомов , электронов, образующих куперовские пары, и т.д. С его помощью описываются свойства теплового излучения, теплоемкость кристаллов и многие другие физические явления. Что же касается поведения обычных газов, атомы которых являются бозе-частицами, то анализ показывает, что при нормальных температурах и давлениях эти газы не являются вырожденными и подчиняются классической статистике. Вырождение наступает либо при очень низких температурах, либо при очень высоких давлениях, т.е. при тех условиях, при которых газы перестают быть идеальными. Таким образом, для этих газов статистика Бозе-Эйнштейна в той области, в которой справедлива кинетическая теория газов, практически не отличается от классической статистики Больцмана.

Билет 53. Фермионы и Бозоны

Установлено, что симметрия или антисимметрия волновых функций определяется спином частиц. В зависимости от характера симметрии все элементарные частицы и построенные из них системы (атомы, молекулы) делятся на два класса: частицы с полуцелым спином (например электроны, нейтроны и протоны) описываются антисимметричными волновыми функциями и подчиняются статистике Ферми–Дирака; эти частицы называются фермионами. Частицы с нулевым, или целочисленным, спином (например фотоны, мезоны) описываются симметричными функциями (волновыми) и подчиняются статистике Бозе–Эйнштейна; эти частицы называются бозонами.

Сложные частицы (например атомные ядра), составленные из нечетного числа фермионов, являются фермионами (суммарный спин – полуцелый), а из четного – бозонами (суммарный спин – целый).

Зависимость характера симметрии волновых функций системы тождественных частиц от спина частиц теоретически обоснована швейцарским физиком В. Паули, что явилось еще одним доказательством того, что спины являются фундаментальной характеристикой микрочастиц.

Билет 54.Электропроводность металлов

Удельное электрическое сопротивление (р) металла — это сопротивление (в омах) столбика металла длиной 1 см с поперечным сечением 1 см2. Величина, обратная удельному сопротивлению, называется удельной электропроводностью и измеряется в обратных омах. При нормальных условиях сопротивление куска металла при данной температуре не зависит от силы тока и этот факт является основой закона Ома, согласно которому сила тока прямо пропорциональна разности потенциалов и обратно пропорциональна сопротивлению данного проводника.

Так как удельное электросопротивление и удельная электропроводность относятся к единице объема, они не очень удобны для обсуждения. Некоторые авторы используют понятие «атомная электропроводность», которая означает удельную электропроводность, деленную на множитель, пропорциональный числу атомов в единице объема.

Если значения для различных металлов при комнатной температуре нанести на график в функции атомного номера, получится отчетливо периодическая кривая, однако результаты осложняются тем, что температура выбрана совершенно произвольно. В одной из ранних работ Бенедикса, Грюнайзена и Бридгмана электропроводности элементов сравнивались при температурах, равных половине характеристической температуры для каждого металла. Это обеспечивает сравнение металлов в приблизительно одинаковых условиях с точки зрения атомных колебаний.

Если построить кривую зависимости атомной электропроводности от атомного номера, обнаруживается отчетливая периодичность, согласно которой наибольшей атомной электропроводностью обладают одновалентные щелочные металлы и одновалентные медь, серебро и золото. Увеличение числа валентных электронов на атом не приводит к более высокой электропроводности. Это в настоящее время объяснено на основе электронной теории. Мы видели, что в изоляторе имеющееся число валентных электронов достаточно как раз для заполнения данной энергетической зоны, которая отделена от следующей, более высокой незанятой зоны энергетическим зазором (запрещенной зоной). Это связано с тем, что электроны в состояниях, соответствующих положению на поверхности зоны Бриллюэна, удовлетворяют условиям брэгговского отражения внутри кристалла. Эти эффекты означают, что увеличение числа электронов, приходящихся на один атом, не означает соответствующего увеличения числа электронов, которые могут эффективно участвовать в результирующем потоке в любом одном направлении.

При переходе от одновалентного элемента к следующему двухвалентному элементу всегда наблюдается резкое падение атомной электропроводности: при переходе от двухвалентного элемента к следующему за ним трехвалентному эффект выражен менее резко. Переходные металлы и элементы, кристаллизующиеся по правилу, имеют относительно низкие электропроводности (на атом), однако при переходе от сурьмы к висмуту (в группе V В) резко возрастает.