
- •1.Интерференция
- •Дифракция света
- •4. Дифракция световых волн:принцип Гюйгенса-Френеля,Дифракция Френеля(Зоны Френеля),Дифракция Фраунгофера,Дифракция на круглом отверстии и на круглом диске
- •6. Дифракционная решетка
- •7 Дисперсия разрешающая способность
- •8. Способы получения поляризованного света
- •9. Эффект керра
- •11 Вопрос
- •12 Вопрос
- •13 Вопрос
- •14 Вопрос
- •15 Вопрос
- •17 Вопрос
- •18 Вопрос
- •19 Вопрос
- •20 Вопрос
- •21)Опыт Боте
- •22)Фотоэффект (внешний)
- •26) Формула Ридберга
- •Обобщённый принцип неопределённости
- •Общие наблюдаемые переменные, которые повинуются принципу неопределённости
- •31. Уравнение Шрёдингера.
- •32. Пси функция.
- •33. Потенциальная яма.
- •35. Атом водорода
- •36.Штерна-Герлаха опыт
- •39.Квантовые числа.
- •44 Колебательно-вращательный спектр
39.Квантовые числа.
Ква́нтовое число́ в квантовой механике — численное значение какой-либо квантованной переменной микроскопического объекта (элементарной частицы, ядра, атома и т. д.), характеризующее состояние частицы. Задание квантовых чисел полностью характеризует состояние частицы.
Некоторые квантовые числа связаны с движением в пространстве и характеризуют пространственное распределение волновой функции частицы. Это, например, радиальное (главное) (nr), орбитальное (l) и магнитное (m) квантовые числа электрона в атоме, которые определяются как число узлов радиальной волновой функции, значение орбитального углового момента и его проекция на заданную ось, соответственно.
Некоторые другие квантовые числа никак не связаны с перемещением в обычном пространстве, а отражают «внутреннее» состояние частицы. К таким квантовым числам относится спин и его проекция.
Квантовые числа — энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.
Главное квaнтовое число n определяет общую энергию электрона и степень его удаления от ядра (номер энергетического уровня); оно принимает любые целочисленные значения, начиная с 1(n = 1, 2, 3, . . .)
Орбитальное (побочное или азимутальное) квантовое число l определяет форму атомной орбитали. Оно может принимать целочисленные значения от 0 до n-1 (l = 0, 1, 2, 3,..., n-1). Каждому значению l соответствует орбиталь особой формы. Орбитали с l = 0 называются s-орбиталями, l = 1 – р-орбиталями (3 типа, отличающихся магнитным квантовым числом m), l = 2 – d-орбиталями (5 типов), l = 3 – f-орбиталями (7 типов).
Магнитное квантовое число m определяет ориентацию орбитали в пространстве относительно внешнего магнитного или электрического поля. Его значения изменяются от +l до -l, включая 0. Например, при l = 1 число m принимает 3 значения: +1, 0, -1, поэтому существуют 3 типа р-АО: рx, рy, рz.
Спиновое квантовое число s может принимать лишь два возможных значения +1/2 и -1/2. Они соответствуют двум возможным и противоположным друг другу направлениям собственного магнитного момента электрона, называемого спином (от англ. веретено). Для обозначения электронов с различными спинами используются символы:
 и
и  .
.
Билет 40. Эффект Зеемана
р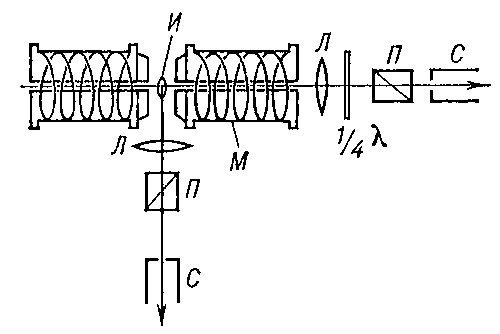 асщепление
спектральных линий под действием
магнитного поля. Для наблюдения З. э.
источник света, испускающий линейчатый
спектр, располагается между полюсами
мощного электромагнита (рис. 1) . При этом
каждая спектральная линия расщепляется
на несколько составляющих. Расщепление
весьма незначительно (для магнитных
полей Зеемана эффект 20 кэ составляет
несколько десятых Å),
поэтому для наблюдения З. э. применяют
спектральные приборы с высокой разрешающей
способностью.
асщепление
спектральных линий под действием
магнитного поля. Для наблюдения З. э.
источник света, испускающий линейчатый
спектр, располагается между полюсами
мощного электромагнита (рис. 1) . При этом
каждая спектральная линия расщепляется
на несколько составляющих. Расщепление
весьма незначительно (для магнитных
полей Зеемана эффект 20 кэ составляет
несколько десятых Å),
поэтому для наблюдения З. э. применяют
спектральные приборы с высокой разрешающей
способностью.
Все компоненты
зеемановского расщепления . Картина
расщепления и поляризация компонент
зависят от направления наблюдения. В
простейшем случае в направлении,
перпендикулярном направлению магнитного
поля (поперечный З. э.), обнаруживаются
(рис. 2) 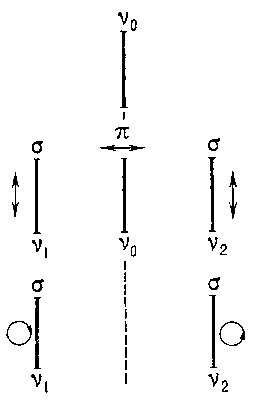 3
линии: несмещенная π-компонента,
поляризованная по направлению поля, и
2 симметрично по отношению к ней
расположенные σ-компоненты, поляризованные
перпендикулярно полю. При наблюдении
в направлении поля (продольный З. э.)
остаются только σ-компоненты, поляризованные
в этом случае по кругу.
3
линии: несмещенная π-компонента,
поляризованная по направлению поля, и
2 симметрично по отношению к ней
расположенные σ-компоненты, поляризованные
перпендикулярно полю. При наблюдении
в направлении поля (продольный З. э.)
остаются только σ-компоненты, поляризованные
в этом случае по кругу.
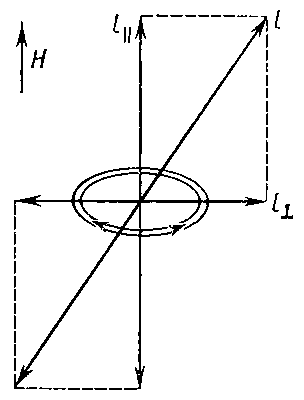 Первое объяснение З.
э. дал Г. Лоренц в 1897. Он рассматривал
электрон в атоме как гармонический
осциллятор частоты излучающий в
отсутствие внешнего поля спектральную
линию этой частоты. В однородном внешнем
магнитном поле Н движение линейно
колеблющегося электрона можно разложить
на линейное колебание вдоль направления
поля и два круговых колебания (с
противоположными направлениями вращения)
в плоскости, перпендикулярной Н (рис.
3). На линейное колебание поле Н не
действует, и его частота остаётся равной
v0; частоты круговых составляющих
изменяются, т.к. электрон в магнитном
поле получает дополнит. вращение вокруг
направления магнитного поля с частотой
Δv = 1/4π(e/me) Н,
где е/ме — отношение заряда электрона
к его массе (см. Лармора прецессия).
Частоты этих колебаний становятся
равными v1 = v0 + Δv и
v2 =vo — Δv. Т. о., атом
в магнитном поле испускает 3 линии с
частотами v0, v1 и v2 (зеемановский триплет).
Такая картина расщепления — простой
(или нормальный) З. э. — получается только
для одиночных спектральных линий (см.
Атомные спектры), а также в предельном
случае очень сильных магнитных полей
(эффект Пашена — Бака). Как правило,
наблюдается более сложная картина:
спектральная линия расщепляется на
большее число компонент с различными
значениями Δv — сложный (или аномальный)
З. э.; получается спектральная группа
равноотстоящих π-компонент и две
симметрично от неё расположенные группы
равноотстоящих σ-компонент. Полное
объяснение З. э. даёт квантовая теория.
Квантовая система, например атом,
обладает магнитным моментом μ, который
связан с механическим моментом количества
движения М и может ориентироваться в
магнитном поле только определённым
образом. Число возможных ориентаций μ
равно степени вырождения уровня энергии
(см. Вырождение), т. е. числу возможных
состояний атома с данной энергией Е. В
магнитном поле каждой ориентации μ
соответствует своя дополнительная
энергия ΔЕ. Это приводит к снятию
вырождения — уровень расщепляется.
Первое объяснение З.
э. дал Г. Лоренц в 1897. Он рассматривал
электрон в атоме как гармонический
осциллятор частоты излучающий в
отсутствие внешнего поля спектральную
линию этой частоты. В однородном внешнем
магнитном поле Н движение линейно
колеблющегося электрона можно разложить
на линейное колебание вдоль направления
поля и два круговых колебания (с
противоположными направлениями вращения)
в плоскости, перпендикулярной Н (рис.
3). На линейное колебание поле Н не
действует, и его частота остаётся равной
v0; частоты круговых составляющих
изменяются, т.к. электрон в магнитном
поле получает дополнит. вращение вокруг
направления магнитного поля с частотой
Δv = 1/4π(e/me) Н,
где е/ме — отношение заряда электрона
к его массе (см. Лармора прецессия).
Частоты этих колебаний становятся
равными v1 = v0 + Δv и
v2 =vo — Δv. Т. о., атом
в магнитном поле испускает 3 линии с
частотами v0, v1 и v2 (зеемановский триплет).
Такая картина расщепления — простой
(или нормальный) З. э. — получается только
для одиночных спектральных линий (см.
Атомные спектры), а также в предельном
случае очень сильных магнитных полей
(эффект Пашена — Бака). Как правило,
наблюдается более сложная картина:
спектральная линия расщепляется на
большее число компонент с различными
значениями Δv — сложный (или аномальный)
З. э.; получается спектральная группа
равноотстоящих π-компонент и две
симметрично от неё расположенные группы
равноотстоящих σ-компонент. Полное
объяснение З. э. даёт квантовая теория.
Квантовая система, например атом,
обладает магнитным моментом μ, который
связан с механическим моментом количества
движения М и может ориентироваться в
магнитном поле только определённым
образом. Число возможных ориентаций μ
равно степени вырождения уровня энергии
(см. Вырождение), т. е. числу возможных
состояний атома с данной энергией Е. В
магнитном поле каждой ориентации μ
соответствует своя дополнительная
энергия ΔЕ. Это приводит к снятию
вырождения — уровень расщепляется.
Билет 41. Принцип Паули
Принцип Паули, который часто называют еще принципом запрета, ограничивает число электронов, которые могут находиться на одной орбитали. Согласно принципу Паули, на любой орбитали может находиться не более двух электронов и то лишь в том случае, если они имеют противоположные спины (неодинаковые спиновые числа). Поэтому в атоме не должно быть двух электронов с одинаковыми четырьмя квантовыми числами (n, l, ml, ms).
Атом
лития имеет три электрона. Орбиталь с
самой низкой энергией - 1s-орбиталь -
может быть заселена лишь двумя электронами,
причем у этих электронов должны быть
разные спины. Если обозначать спин +1/2
стрелкой, направленной вверх, а спин
−1/2 - стрелкой, направленной вниз, то
два электрона с противоположными
(антипараллельными) спинами на одной
орбитали можно схематически представить
так:
![]()
Третий электрон в атоме лития должен занимать орбиталь, следующую по энергии за самой низкой орбиталью, то есть 2s-орбиталь.
Билет 42. Энергия молекул
Вспомним, что температура связана со средней энергией (приходящейся на одну молекулу) только поступательных степеней свободы молекулы:
![]() ,где k — постоянная
Больцмана. В этой записи учтен так
называемый принцип равнораспределения
энергии по степеням свободы: на каждую
поступательную степень свободы при
термодинамическом равновесии приходится
в среднем энергия
,где k — постоянная
Больцмана. В этой записи учтен так
называемый принцип равнораспределения
энергии по степеням свободы: на каждую
поступательную степень свободы при
термодинамическом равновесии приходится
в среднем энергия
![]() .
Этот принцип иногда называют теоремой,
иногда законом, иногда постулатом о
равнораспределении энергии по степеням
свободы. Важно не название. Важно другое
— что он распространяется не только на
поступательные, но и на любые степени
свободы молекулы. Это означает, что для
нагревания до температуры Т газа,
молекулы которого обладают при этой
температуре i степенями свободы, нужно
каждую из них «накормить» энергией
. Так что в результате потребуется в
среднем, в расчете на одну молекулу,
энергия
.
Этот принцип иногда называют теоремой,
иногда законом, иногда постулатом о
равнораспределении энергии по степеням
свободы. Важно не название. Важно другое
— что он распространяется не только на
поступательные, но и на любые степени
свободы молекулы. Это означает, что для
нагревания до температуры Т газа,
молекулы которого обладают при этой
температуре i степенями свободы, нужно
каждую из них «накормить» энергией
. Так что в результате потребуется в
среднем, в расчете на одну молекулу,
энергия
![]()
,в
расчете на один моль, содержащий число
молекул, равное постоянной Авогадро
NA, -
![]() ,где R — универсальная газовая постоянная,
в расчете на один килограмм —
,где R — универсальная газовая постоянная,
в расчете на один килограмм —
![]() ,где М — молярная масса. Напомним, что
множитель при Т называется среднемолекулярной,
молярной или удельной теплоемкостью
соответственно.
,где М — молярная масса. Напомним, что
множитель при Т называется среднемолекулярной,
молярной или удельной теплоемкостью
соответственно.
Вернемся к колебательному движению молекул. Сколько степеней свободы соответствуют колебаниям вдоль одной линии? Оказывается, две: нужно знать не только положение относительно равновесия, но и скорость. С точки зрения энергии: одинаковый вклад ( ) дает как средняя кинетическая энергия атомов, так и средняя потенциальная энергия их взаимодействия. Таким образом, если для жесткой гантельки i = 5, то в случае замены жесткого стерженька одномерной пружинкой i = 7.
Билет 43.
Несферические ядра, помимо колебательных уровней в спектре возбуждения и уровней, связанных с переходами нуклонов ядра на более высокие оболочки, имеют также уровни в спектрах возбуждения, которые имеют вращательную природу. Уровни спектров возбуждения, возникающие вследствие вращения несферических ядер, имеют ряд характерных особенностей; последовательность таких уровней часто называют вращательной полосой. Пример вращательной полосы для четно- четного ядра 170Hf показан на рис. 7.5.
|
Энергии уровней вращательной полосы можно получить в результате решения уравнения Шредингера с гамильтонианом, отражающим вращательные степени свободы ядра. Следует подчеркнуть, что, согласно квантовой теории, вращательные степени свободы присущи исключительно несферическим объектам.

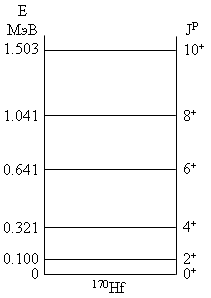 Рис.
7.5.
Вращательная полоса ядра 170Hf
.
Рис.
7.5.
Вращательная полоса ядра 170Hf
.