31. Уравнение Шрёдингера.

Уравне́ние Шрёдингера — уравнение, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах. Его можно назвать уравнением движения квантовой частицы. Установлено Эрвином Шрёдингером в 1926 году.

Позволяет найти волновые функции частиц, движущихся в различных силовых полях.

  ,   — постоянная Планка;   — масса частицы,   —потенциальная энергия частицы,   —оператор Лапласа, результат действия которого на некоторую функцию представляет собой сумму вторых частных производных по координатам:

Из уравнения (1) следует, что вид волновой функции определяется функцией , т.е. характером сил, действующих на частицу.

частное решение для специального случая, когда   не является функцией времени, можно записать в виде:

где функция   должна удовлетворять уравнению:

которое получается из уравнения Шрёдингера (1) при подстановке в него указанной выше формулы для   (2)

32. Пси функция.

Волнова́я фу́нкция (функция состояния, пси-функция) — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния квантовомеханической системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):

где  — координатный базисный вектор, а  — волновая функция в координатном представлении.

Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния.

В координатном представлении волновая функция зависит от координат (или обобщённых координат) системы. Физический смысл приписывается квадрату её модуля , который интерпретируется как плотность вероятности (для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами в момент времени :

.

Тогда в заданном квантовом состоянии системы, описываемом волновой функцией , можно рассчитать вероятность того, что частица будет обнаружена в любой области пространства конечного объема :

Волновая функция по своему смыслу должна удовлетворять так называемому условию нормировки, например, в координатном представлении имеющее вид:

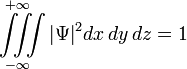
Это условие выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией где-либо во всём пространстве равна единице. В общем случае интегрирование должно производиться по всем переменным, от которых зависит волновая функция в данном представлении.

33. Потенциальная яма.

Потенциальная яма – область пространства, где присутствует локальный минимум потенциальной энергии частицы. Термин "П. я." происходит от вида графика, изображающего зависимость потенциальной энергии V частицы, находящейся в силовом поле, от её положения в пространстве (в случае одномерного движения — от координаты х; рис. 1).

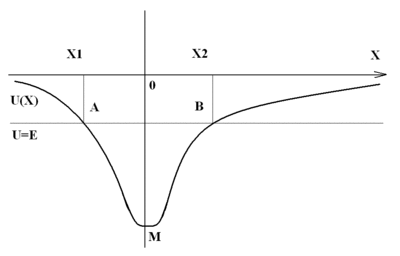
Характеристики П. я. — ширина (расстояние, на котором проявляется действие сил притяжения) и глубина (равная разности потенциальных энергий частицы на "краю" ямы и на её "дне", соответствующем минимальной потенциальной энергии). Основное свойство П. я. — способность удерживать частицу, полная энергия E которой меньше глубины ямы V₀; такая частица внутри П. я. будет находиться в связанном состоянии.

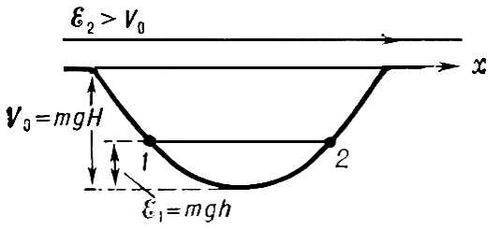
В классической механике частица с энергией E < V₀ не сможет вылететь из П. я. и будет всё время двигаться в ограниченной области пространства внутри ямы; устойчивому равновесию отвечает положение частицы на "дне" ямы (оно достигается при кинетической энергии частицы Екин = E — V = 0). Если же E > V₀, то частица преодолеет действие сил притяжения и покинет яму. Примером может служить движение упругого шарика, находящегося в поле сил земного притяжения, в чашке с пологими стенками (рис. 2).

В квантовой механике, в отличие от классической, энергия частицы, находящейся в связанном состоянии в П. я., может принимать лишь определённые дискретные значения, т. е. существуют дискретные уровни энергии (см., например, рис. 6 к ст. Квантовая механика). Однако такая дискретность уровней становится заметной лишь для систем, имеющих микроскопические размеры и массы. По порядку величины расстояние DE между уровнями энергии для частицы массы m в "глубокой" яме ширины а определяется величиной DE ~ /ma² ( — Планка постоянная). Наинизший (основной) уровень энергии лежит выше "дна" П. я. (см. Нулевая энергия). В П. я. малой глубины (V_o £ /ma²) связанное состояние может вообще отсутствовать (так, протон и нейтрон с параллельными спинами не образуют связанной системы, несмотря на существование сил притяжения между ними).

Кроме того, согласно квантовой механике, частица, находящаяся в П. я. со "стенками" конечной толщины (типа кратера вулкана), может покинуть П. я. за счёт туннельного эффекта даже в том случае, если её энергия меньше высоты ямы (ср. со ст. Потенциальный барьер).

Форма П. я. и её размеры (глубина и ширина) определяются физической природой взаимодействия частиц. Важный случай — кулоновская П. я., описывающая притяжение атомного электрона ядром. Понятие "П. я." широко применяется в атомной и молекулярной физике, а также в физике твёрдого тела и атомного ядра.

3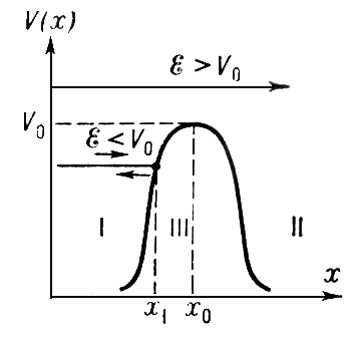 4. Потенциальный барьер в физике, пространственно ограниченная область высокой потенциальной энергии частицы в силовом поле, по обе стороны которой потенциальная энергия более или менее резко спадает. П. б. соответствует силам отталкивания.

На рис. изображен П. б. простой формы для случая одномерного (по оси х)движения частицы. В некоторой точке х = x₀ потенциальная энергия V (х) принимает максимальное значение V₀, называется высотой П. б. П. б. делит пространство на две области (I и II), в которых потенциальная энергия частицы меньше, чем внутри П. б. (в области III).

В классической механике прохождение частицы через П. б. возможно лишь в том случае, если её полная (кинетическая + потенциальная) энергия E превышает высоту П. б. E ³ V₀; тогда частица пролетает над барьером. Если же энергия частицы недостаточна для преодоления барьера, E < V₀, то в некоторой точке x₁ частица, движущаяся слева направо, останавливается и затем движется в обратном направлении. То есть П. б. является как бы непрозрачной стенкой, барьером, для частиц с энергией, меньшей высоты П. б., — отсюда название "П. б.".

В квантовой механике, в отличие от классической, возможно прохождение через П. б. частиц с энергией E < V₀ (это явление называется туннельным эффектом) и отражение от П. б. частиц с E > V₀. Такие особенности поведения частиц в квантовой физике непосредственно связаны с корпускулярно-волновой природой микрочастиц (см. Квантовая механика). Туннельный эффект существен лишь для систем, имеющих микроскопические размеры и массы. Чем уже П. б. и чем меньше разность между высотой П. б. и полной энергией частицы, тем больше вероятность для частицы пройти через него.