Обобщённый принцип неопределённости

Теорема. Для любых самосопряжённых операторов: и , и любого элемента x из H такого, что ABx и BAx оба определены (то есть, в частности, Ax и Bx также определены), имеем:

Это прямое следствие неравенства Коши — Буняковского.

Следовательно, верна следующая общая форма принципа неопределённости, впервые выведенная в 1930 г. Говардом Перси Робертсоном и (независимо) Эрвином Шрёдингером:

Это неравенство называют соотношением Робертсона — Шрёдингера.

Оператор AB − BA называют коммутатором A и B и обозначают как [A,B]. Он определен для тех x, для которых определены оба ABx и BAx.

Из соотношения Робертсона — Шрёдингера немедленно следует соотношение неопределённости Гейзенберга:

Предположим, A и B — две физические величины, которые связаны с самосопряжёнными операторами. Если ABψ и BAψ определены, тогда:

,

где:

— среднее значение оператора величины X в состоянии ψ системы, и

— оператор стандартного отклонения величины X в состоянии ψ системы.

Приведённые выше определения среднего и стандартного отклонения формально определены исключительно в терминах теории операторов. Утверждение становится однако более значащим, как только мы заметим, что они являются фактически средним и стандартным отклонением измеренного распределения значений. См. квантовая статистическая механика.

То же самое может быть сделано не только для пары сопряжённых операторов (например координаты и импульса, или продолжительности и энергии), но вообще для любой пары Эрмитовых операторов. Существует отношение неопределённости между напряжённостью поля и числом частиц, которое приводит к явлению виртуальных частиц.

Возможно также существование двух некоммутирующих самосопряжённых операторов A и B, которые имеют один и тот же собственный вектор ψ. В этом случае ψ представляет собой чистое состояние, которое является одновременно измеримым для A и B.

Общие наблюдаемые переменные, которые повинуются принципу неопределённости

Предыдущие математические результаты показывают, как найти отношения неопределённости между физическими переменными, а именно, определить значения пар переменных A и B, коммутатор которых имеет определённые аналитические свойства.

• самое известное отношение неопределённости — между координатой и импульсом частицы в пространстве:

• отношение неопределённости между двумя ортогональными компонентами оператора полного углового момента частицы:

где i, j, k различны и J_i обозначает угловой момент вдоль оси x_i.

• следующее отношение неопределённости между энергией и временем часто представляется в учебниках физики, хотя его интерпретация требует осторожности, так как не существует оператора, представляющего время:

• Следует подчеркнуть, что для выполнения условий теоремы, необходимо, чтобы оба самосопряженных оператора были определены на одном и том же множестве функций. Примером пары операторов, для которых это условие нарушается, может служить оператор проекции углового момента L_z и оператор азимутального угла 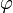. Первый из них является самосопряженным только на множестве 2π-периодичных функций, в то время как оператор , очевидно, выводит из этого множества. Для решения возникшей проблемы можно вместо взять 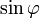, что приведет к следующей форме принципа неопределенности^[1]:

.

Однако, при условие периодичности несущественно и принцип неопределенности принимает привычный вид:

.