4.4. Расчет посадок по теории вероятности

Получение сопряжений с заданным зазором в подвижных посадках или с заданным натягом в неподвижных посадках, а также зазора или натяга в переходных посадках при сборке, является случайным событием, а сами величины зазоров или натягов - случайными. При этом важно знать, какова степень возможности получения сопряжений с зазором или натягом в заданных пределах, либо зазора или натяга для переходных посадок.

Степень возможности появления случайных событий или величин оценивается вероятностью.

В посадках случайной величиной является разность Δ = Dr – dr

Если Δ< 0, имеем натяг, если Δ > 0 - зазор. Чтобы определить вероятность получения при сборке величины Δ в заданных пределах, надо знать, кроме предельных отклонений, закон распределения размеров сопрягаемых деталей в пределах допуска. В машиностроении наибольшее применение имеет закон нормального распределения, выражающийся уравнением

у=_е(х-х)²/2σ²/σ√2π (6)

где у - плотность вероятности, σ - среднее квадратическое отклонение случайной величины; х - случайная величина; х -среднее арифметическое значение случайной величины; е = 2,718 - основание натуральных логарифмов.

Случайными величинами могут быть размеры деталей, отклонения, зазоры, натяги и др. Для расчетов этот закон применяется в преобразованном виде, получаемом путем замены рассматриваемой величины х безразмерной z

z=(х-х)/ σ

Уравнение (6) после замены будет иметь вид

у=_е(-z)²/2/σ√2π (7)

Задаваясь значениями z = 0; 0,2; 0,5; 1,0; 1,5; 2; 3, находят у

На рис.4.2 дано графическое изображение этой функции.

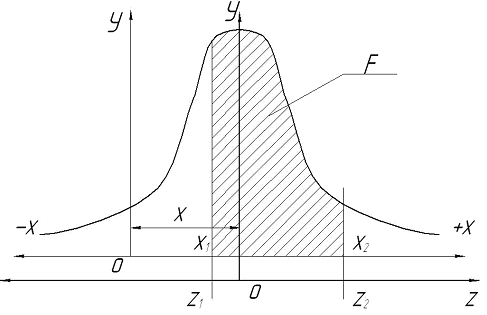
Рис. 4.2 Кривая нормального распределения.

Вероятность того, что случайная величина x примет значение, находящееся в пределах X1 ≤ X ≤ X2 определяется заштрихованной площадью F. Значениям X1 и Х2 соответствуют значения Z1 и Z2

z₁=(х₁-х)/ σ; z₂=(х₂-х)/ σ

Площадь F определяется так:

F=_x1∫^x2 ydx; dz=dz/σ;

Обозначим

=Ф(z)

получим

F= Ф(z₂)- Ф(z₁)

Значения интеграла Ф(z) приведены в приложении П1, из которого находим, что Ф (3) == 0,49865 при z = 3. Поскольку вся площадь, ограниченная кривой нормального распределения, представляет собой 2Ф(z) = 1, а Ф(3) - Ф(-3) = 2·0,498651, то безразмерная случайная величина практически не может выходить за пределы 3 ≤ z≤-3

При изготовлении деталей размеры их не могут выходить за предельные dнб и dнм которым соответствуют вышеуказанные значения случайной величины z т.е.

zнб =( dнб – d)/ σ=3

zнм=( dнм – d)/ σ=-3

Вычитая из первого уравнения второе, получим

dнб - dнм=T=6σ

При известном допуске на размер среднее квадратическое отклонение σ = Т/6. В посадках определяется разность двух случайных величин Dr и dr

Из теории вероятности известно, что если две или несколько случайных величин подчиняются закону нормального распределения, то сумма или разность их также подчиняется этому закону, а среднее квадратическое отклонение суммы или разности их находится по формуле

σ_∑=

где σ1 и σ2 - средние квадратические отклонения случайных величин 1 и 2.

Применительно к посадкам получим

σ_П=

Среднее арифметическое значение случайной величины для посадки определяется следующим образом

Δ=(D_c-d_c)/2=(ES+EI)/2 –(es+ei)/2

Из вышеизложенного видно, что для использования закона нормального распределения при расчете вероятности любых случайных величин надо знать среднее арифметическое значение случайной величины, среднее квадратическое отклонение случайной величины, граничные значения случайной величины.