50) назначение и возможности пакета маткад.

Mathcad – программное средство, среда для выполнения разнообразных математических расчетов, предоставляющая пользователю инструменты для работы с формулами, числами, текстами и графиками.

Mathcad позволяет выполнять как численные, так и аналитические вычисления, имеет удобный математико-ориентированный интерфейс и средства графики. Может оказать помощь в решении математических задач. Mathcad сочетает в себе возможности проведения расчетов и подготовки форматированных научных и технических документов.

В Mathcad предусмотрены панели инструментов, с помощью которых удобно вводить специальные символы. Построение графиков, вычисление интегралов и другие сложные операции выполняются заполнением в документе помеченных позиций.

Данная среда содержит:

• обширную библиотеку встроенных математических функций;

• инструменты построения двумерных и трехмерных графиков различных типов;

• средства создания текстов;

• программные конструкции, позволяющие писать программы для решения задач, которые сложно решать стандартными инструментами.

51) задание векторов и матриц в маткад и действия с ними

Векторы и матрицы рассматриваются в программе Mathcad как одномерные и двумерные массивы данных.

Матрица создается с помощью диалогового окна Вставить матрицу (рис. 1.6), которое открывают командой Вставка > Матрица (Insert > Matrix) или первой кнопкой на панели "Матрица" (рис. 1.7). Вектор задается как матрица, имеющая один столбец. В диалоговом окне задается число строк и столбцов, а после вставки на рабочий лист матрица содержит вместо элементов заполнители, вместо которых следует вставить число, переменную или выражение.

Рис. 1.6	Рис. 1.7

Для матриц определены сложение, умножение на число, перемножение и другие операции. Допустимо использование матриц вместо скалярных выражений: в этом случае предполагается, что указанные действия должны быть применены к каждому элементу матрицы, и результат также представляется в виде матрицы:

Для работы с элементами матрицы используют индексы элементов. Нумерация строк и столбцов матрицы начинается с нуля, что задается системной переменной ORIGIN, и может быть изменено пользователем (например, блок ORIGIN:=1 устанавливает начальный индекс равным единице). Индекс элемента задается числом, переменной или выражением и отображается как нижний индекс. Он вводится после щелчка на кнопке Индекс (Subscript, x_n) на панели инструментов Mатрица (Matrix) или нажатием символа "[" после имени массива (см. приложение "Горячие клавиши"). Индексы двумерных матриц записываются через запятую.

Иногда (например, при построении графиков) требуется выделить вектор, представляющий собой столбец матрицы. Номер столбца матрицы отображается как верхний индекс, заключенный в угловые скобки:  . Для его ввода используется кнопка Столбец (Matrix Column) на панели инструментов Матрица или соответствующая "горячая" клавиша.

Для задания некоторой последовательности элементов матрицы используют диапазоны. Диапазон фактически представляет собой вектор, содержащий арифметическую прогрессию, определенную первым, вторым и последним элементами. Чтобы задать диапазон, следует указать значение первого элемента, через запятую значение второго и через точку с запятой значение последнего элемента. Точка с запятой при задании диапазона отображается как две точки (..). Диапазон можно использовать как значение переменной, например х:=0,0.01..1. Если разность прогрессии равна единице (то есть, элементы просто нумеруются), значение второго элемента и соответствующую запятую опускают.

52) способы решения слау в маткад.

Решение систем линейных уравнений с помощью функции lsolve.

Для решения систем линейных уравнений в MathCAD существует встроенная функция lsolve(A,B), которая возвращает вектор X для системы линейных уравнений при заданной матрице коэффициентов и векторе свободных членов.

Для решения системы линейных уравнений с помощью функции lsolve необходимо создать матрицу коэффициентов системы линейных уравнений.

Рисунок 5.1 - Матрица составленная из коэффициентов системы линейных уравнений

Далее создаем вектор свободных членов системы линейных уравнений «b». Вектор задается тем же образом, что и матрица, но размерностью в один столбец и четыре строки.

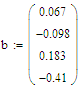
Рисунок 7.2 – Вектор свободных членов системы линейных уравнений

За тем решим систему с помощью функции lsolve. Для этого записываем следующее:

Рисунок 7.3 – Вектор soln для системы линейных уравнений при заданной матрице и векторе свободных членов.

После, выводим полученный вектор, содержащий корни системы,  с помощью знака «=».

Рисунок 7.4 – Вектор содержащий корни систем

6 Решение системы линейных уравнений по формулам Крамера.

Создаем матрицу и вектор свободных членов как в предыдущем способе решения системы уравнений. Далее нам необходимо найти определитель матрицы, считаем его в программном пакете, он равен:

Рисунок 6.1 – Результат вычисления определителя

После, заменяем в созданной матрице первый столбец вектором  свободных членов, используя операцию выделения столбца матрицы и вычисляем её определитель. Аналогично из матрицы коэффициентов создать матрицу, в которой второй столбец заменен вектором свободных членов. В нашем случае данную операцию необходимо выполнить 4 раза.

Рисунок 6.2 – Замена столбца исходной матрицы на солбец свободных членов и значение определителей для полученных матриц.

За тем, находим корень уравнения, разделив определитель матрицы с замененным первым столбцом на определитель матрицы коэффициентов. Остальные корни системы уравнений найдем аналогично.

Рисунок 8.4 – Корни уравнения

7 Решение системы линейных уравнений методом Гаусса.

Для того, чтобы решить систему методом Гаусса составляем основную матрицу и вектор свободных членов как и в предыдущих решениях.

Рисунок 9.1 – Матрица и вектор-столбец свободных членов

За тем, сформируем расширенную матрицу системы, для этого воспользуемся функцией augment(A,b) – она добавляет к столбцам матрицы системы уравнений справа вектор – столбец свободных членов. Таким образом, в поле ввода ввести Ar:=, затем выбрать меню «Вставить» - «Функция» - augment, в первых двух темных квадратах задать значения A и b. И выводим расширенную матрицу системы.

Рисунок 9.2 – Добавление к системе уравнений вектора – столбца свободных членов и вывод расширенной матрицы

Далее, приводим расширенную матрицу системы к ступенчатому виду, для чего воспользуемся встроенной функцией rref(A), которая приводит матрицу к ступенчатому виду с единичным базисным минором. То есть в поле ввода задать «Ag:=», выбрать из списка функций функцию «rref», в темном квадрате задать значение «Ar». И вывести расширенную матрицу системы в ступенчатом виде.

Рисунок 9.3 – Приведение матрицы к ступенчатому виду с единичным базисным минором и сама расширенная матрица системы в ступенчатом виде.

За тем сформируем вектор – столбец решения системы уравнений при помощи функции submatrix(A, ir, jr, ic, jc), где ir, jr – начальная и конечная для выделения строки, а ic, jc – начальный и конечный для выделения столбца. То есть, мы выводим блок матрицы «А» с элементами расположенными в строках c ir по jr и столбцах с ic по jc. Для этого в поле ввода с клавиатуры вводим x:=, выбираем функцию submatrix, в значении которой через запятую задаем соответственно значения 1, 4, 5, 5. Далее, выводим вектор – столбец решения системы уравнений.

Рисунок 9.4 - Формирование вектора при помощи функции submatrix и сам вектор – столбец решения системы уравнений

53) графики функций в маткад