15. Числовые характеристики вариационного ряда. Построение гистограмм частот и относительных частот.

Отдельные значения, снимаемые с карты в ряде точек, называются вариантами (xi), т.е. из совокупности значений извлечена выборка, а наблюдаемые значения (xi) называются вариантами, которые образуют статистические ряды.

Ряды могут быть сгруппированы и ранжированы по определенным числовым интервалам. Аналогии такой группировки на карте может служить любая равномерная ступенчатая шкала. Ступени шкалы соответствуют интервалам группировки. Число- вариант в каждом интервале называется частотой (ni). Отношение частоты к объему выборки называется относительной частотой (Wi):

Wi= ni / n, где n – выборка

Или относительная частота определяется в процентах(%):

Wi= ni / n * 100%

Рассмотрим пример, с целью изучения совокупности рек на данном участке карты по их длине измеряем длину (L) всех рек.

Этот статистический ряд, его численность = 60 (выборка). При достаточном количестве наблюдений, с целью изучения характера изменчивости признака, статистический ряд может быть разделен на группы. Возмем для этого разность крайних значений признака Xmin= 5, Xmax= 165, разность = 160. Разделим на 8 групп (например) с интервалом 20 мм в каждой группе.

Число членов каждой группы, находящейся в определенном интервале значения признака, называется частотой.

Доля объектов с данным значением признака или просто отношение частоты к числу членов в совокупности называется относительной частотой или частностью.

В таблице 2 приведен сгруппированный ряд или статистическая совокупность. Если требуется узнать ту часть совокупности, которая находится в различных пределах значения признака, то последовательно суммируют частоты каждого интервала и получают, таким образом, накопленные частоты (частости).

Для наглядности представления сгруппированного ряда служат различные графики статистического распределения, в частности полигон и гистограмма.

Полигоном частот называют ломанную, отрезки которой соединяют точки (x1,y1),(x2,y2),…( xk,yk).

Для построения полигона частот на оси абсцисс откладывают варианты xi, а на ось ординат – соответствующие им частоты ni. Точки (xi, ni) соединяют отрезками прямых и получают полигон частот.

Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (x1,w1),(x2,w2),…( xk,wk).

Рисунок 1. Полигон и гистограмма частот.

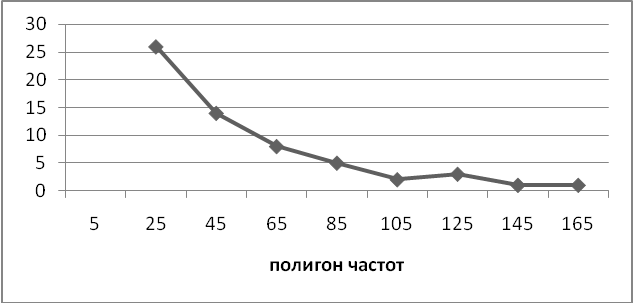
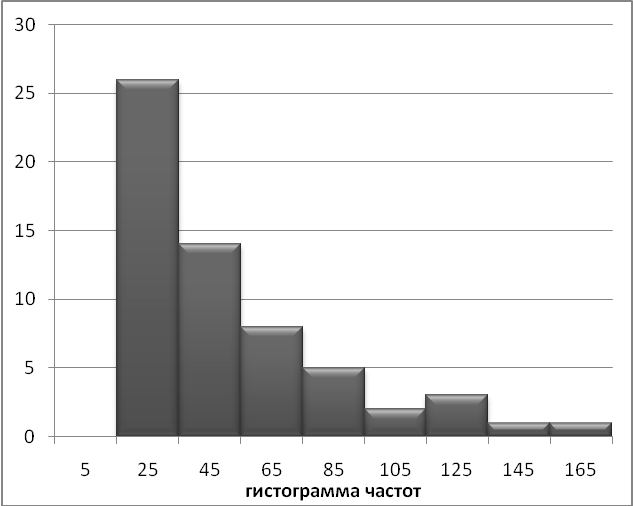
Аналогично строится полигон относительных частот (частостей).

Непрерывное изменение признака более правильно передается гистограммой, на которой частота или частость изображается прямоугольником с основанием равным ширине интервала и высотой равной частоте (частости).

В случае необходимости статистический ряд группируют также по неравным интервалам, тогда для правильной характеристики распределение значений признака вместо частот и частостей вычисляется по плотности распределения, т.е. количество случаев или их доля на единицу ширины интервала.

16. Методы классификации пространственных данных. Построение гистограмм по плотности распределения.

Методы классификации пространственных данных, разнообразны. Классификация объектов, основанная на группировки значений одного из полей атрибутивной таблицы часто применяется при построении картограмм, картодиаграмм и значковых карт. В ГИС возможно автоматическое выделение интервалов, шкал, при этом построенные шкалы могут быть постоянными или переменными интервалами.

Границы ступеней шкалы, определяются на основе числовых характеристик характерных точек статистического (вариационного) ряда, составленного из значений заданного поля отсортированных в порядке возрастания (см. вопрос 17).

Одним из видов группировки статистического ряда, группировка по неравным интервалам, тогда для правильной характеристики распределения значений признака. Вместо частот и частостей вычисляются ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ, т. е. количество случаев или их доля на единицу ширины интервала.

Гистограмма плотности распределения

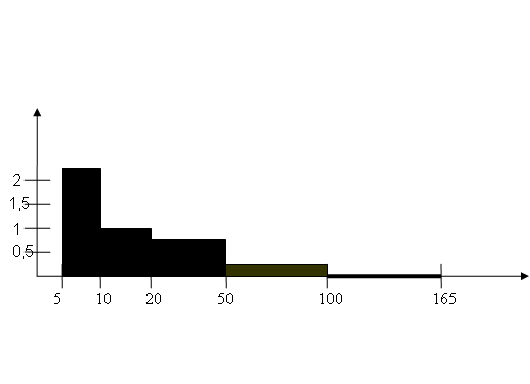
17. Автоматическая классификация объектов по их атрибутивному параметру.

В Гис легко получить (например в ArcView) информацию о числовых, статистических характеристиках значений вариационного поля атрибутивной таблицы: min и max значение; среднее значение х₀; дисперсии D; стандартному отклонению, общему количеству значений n и их сумме.

За нижнюю границу первого интервала принимаются значения х_min, за верхнюю границу х_max; определение всех остальных граничащих значений интервала производится согласно установленному методу классификации (группировки) и заданному числу классов K. Обычно в ГИС используется 5 методов группировки, значений к. л. показателей (атрибута):

1) равных классов (квантилей);

2) равных интервалов;

3) естественных интервалов (границ);

4) равных площадей;

5) стандартных отклонений.

Метод равных классов (квантилей) – устанавливаются границы интервалов, согласно правилу: в каждый класс должно попасть одинаковое количество объектов или приблизительно одинаковое, если отношение n/k не равно целому числу, этот способ используется, когда нужно охарактеризовать группы объектов по величине к. л. показателя, как часть целого.

Метод равных интервалов применяют для построения шкалы с постоянным интервалом, длина интервала L определяется, как величина равная х_min - х_max/K. При большом разбросе в значениях некоторые выделенные интервалы могут оказаться пустыми, т.е. не один объект не попадет в такой интервал.

При использовании метода естественных интервалов их границы определяются по характерным точкам (в местах сравнительно больших значений статического ряда), отмечают естественные скачки в значениях показателей, которые хорошо видны на столбчатых гистограммах построенных по этим значениям. Этот метод подходит для классификации неравно распределенных данных. В большинстве ГИС этот метод применяется по умолчанию.

При использовании метода равных площадей осуществляют разбиение полигональных объектов, определяя точки разбиения так, чтобы общая площадь полигонов в каждом классе была приблизительно одинакова. Сначала рассчитывают общую площадь всех объектов, ее делят на число классов (которые необходимо знать), чтобы определить значение площадей для каждого класса. Этот метод по результатам близок к методу равных классов.

Метод стандартных отклонений основан на значениях двух числовых характеристик статистического ряда, среднем значением х₀ и стандартным отклонением ; Ġ = Границы интервалов устанавливают шагом Ġ или ¼ или ½ по обе стороны от точки х₀, разбиение на классы продолжается до тех пор граничные значения не достигнут предельных х_min и х_max , или не удалятся от среднего на величину ± 3 Ġ. Этот метод характеризует значение объекта в сравнении со средним показателем по всей картографируемой территории.

При выделении интервалов шкал, следует обращать внимание на тип переменных:

1) номинальный; 2) порядковый; 3) интервальный; 4) относительный и на то, как много измеряющая информация обеспечивает шкала их измерения.

Номинальные переменные – используют только для качественной классификации.

Порядковые – позволяют ранжировать (упорядочивать) объекты, указав какие из них в большей или в меньшей степени обладают качественным выражением в данной переменной. Они не позволяют сказать, на сколько больше или на сколько меньше.

Интервальные – позволяют не только упорядочивать объекты переменных, численно выразить и сравнить различия между ними, например, температура измерена в ⁰С образует интервальную шкалу, в такой шкале, следует определить, на сколько одно значение больше другого.

Относительные – схожи с интервальными, характерная особенность – наличие абсолютного нуля, для них верны соотношения Х в 2 раза больше, чем соотношение У, примерами шкал являются измерения во времени и в пространстве.

18. Методы представления географического пространства. Растровая модель

Растровый метод основан на разбиении пространства на множество элементов поверхности. Форма элементов растра может быть различной, но одинаковой по размеру (ячейки). Пространство в таком случае отображается через цепочки соединенных ячеек, представленных, в свою очередь, линиями. Растровые атрибуты не содержат точной координатной информации для объектов географического пространства, поскольку оно поделено на дискретные ячейки одинакового размера. На карте каждой ячейке присвоено 1 значение атрибута, однако число атрибутов может стать сколь угодно большим, если ячейка связана с базой данных. Растровая модель дает информацию о том, что расположен в данной части территории, и чем больше размер ячейки, тем меньше разрешение растра, и соответственно меньше точность положения точек, линий и областей, заключенных в ней.

Растровые модели удобны для хранения и анализа данных, распределенных неравномерно. Растр представляет собой матрицу изображения (х) с присвоенными им кодами, показывающими либо цвет изображения, либо класс объекта. Значения пикселов могут выбираться самостоятельно, в зависимости от изменения вычислений.

К растровым моделям относятся гриды (регулярные сетки), построение которых в ГИС, используют для анализа и моделирования непрерывных распределений данных. Гриды созданы на основе векторных данных, размер растра (разрешение) выбирают в зависимости от масштаба и сложности рисунка местности или карты.

Растровые модели используются для представления различных типов тематической, картографической информации, т.е. для отражения почвенно-растительного покрова, геолого-морфологических характеристик, составления карт плотности населения. Эти модели удобно использовать для выявления взаимосвязей, и часто они являются основными при создании ГИС.

19. Методы представления географического пространства. Векторная модель

Векторная модель – метод основан на присвоении точных пространственных пар координат (х;у) в любой точке. Пространство при этом рассматривается – как непрерывное.

Линии представляются как группы пар координат, связанных вершинами, а области как замкнутая последовательно соединенными линиями, начальная и конечная точек которой совпадают.

Векторная модель – представление объектов набором координатных пар, описывающих геометрические свойства объектов и их пространственную локализацию.

Векторная модель используется для представления точечных, линейных и площадных объектов. Векторные данные хранятся в идее точек и линий, связанных геометрически и математически, они дают информацию, где находится объект.

Векторные модели получаются с использованием дигитайзеров, а растровые – при помощи сканеров.