Растекание жидкости по поверхности твердых тел

Капля жидкости, нанесенная на поверхность, может оставаться на ее определенном участке, и система будет находиться в равновесии в соответствии с законом Юнга: или же растекаться по поверхности так, что краевой угол не устанавливается. В обоих случаях система переходит в состояние с минимальной энергией Гиббса.

Рассмотрим условия растекания жидкости по поверхности. Эти условия сводятся к росту межфазной поверхности на границе жидкость - газ, к росту площади границы раздела жидкость - твердое тело и к уменьшению поверхности твердое тело - газ. Принимая это во внимание, изменение энергии Гиббса можно записать следующим образом: или Для самопроизвольно протекающего процесса dG<0, условием растекания является dS>0. Следовательно, или .

Если разность заменить выражением из уравнения Дюпре, то получим условия растекания в следующем виде:

или

Учитывая, что , получаем

Таким образом, растекание происходит в нашем случае, если работа адгезии превышает работу когезии растекающейся жидкости. Другими словами, жидкость растекается, если её межмолекулярные связи разрушаются в результате адгезии.

Следует отметить, что краевые углы смачивания, существующие в процессе растекания, называются динамическими.

Капиллярные явления при проникновении расплава металла.

При производстве КМ жидкофазным способом армирующие волокна, соприкасаясь друг с другом, образуют капилляры - узкие сосуды, у которых расстояние между стенками соизмеримо с радиусом кривизны поверхности жидкости. Кривизна возникает в результате взаимодействия жидкости со спинками сосуда (адгезия, смачивание). Специфика поведения жидкости в капиллярных сосудах зависит от , смачивает или не смачивает жидкость стенки сосуда. Рассмотрим положение уровней жидкости в двух сосудах на границе раздела трёх фаз.

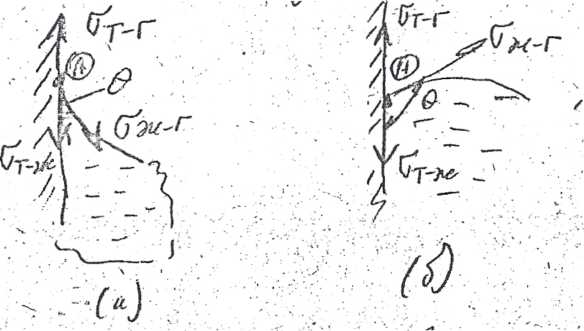
Итак, опять в точке А жидкость подвержена действию трёх сил поверхностного натяжения:

γ_т-ж (на рисунке σ_т-ж) - между стенкой твёрдого тела и жидкостью; σ_т-г - между стенкой и воздухом; σ_ж-г - между жидкостью и воздухом.

Поскольку σ_т-г не равна γ_т-ж, жидкость у точки А может подниматься или опускаться вдоль стенки в зависимости от того, какая из двух сил (γ_т-ж или σ_т-г) окажется большей.

Если σ_т-г ˃γ_т-ж то поверхность раздела примет форму (а), при этом уровень жидкости повысится, и мениск будет вогнутым, то есть имеет место смачивание.

Если же σ_т-г ˂γ_т-ж, , то жидкость у края будет опускаться, и мениск будет выпуклым (б).

Искривление поверхности жидкости создает дополнительное давление, которое не имеет практического значения в широких сосудах, но в капиллярах вызывает поднятие или опускание жидкости на значительную величину. Высота поднятия (или опускания) равна дополнительному (его называют давлением Лапласа) давлению. Чтобы высоту капиллярного поднятия связать с характеристиками смачивания, радиус мениска следует выразить через угол смачивания и радиус капилляра:

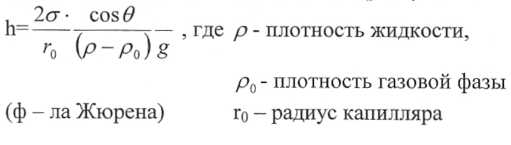
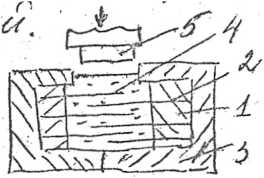
Капиллярные явления имеют большое значение в технике. В частности, при получении КМ методом пропитки, а точнее - компрессионной пропитки. Метод заключается в укладке армирующего каркаса из волокон или частиц в форму, нагрева формы с каркасом, заливке в форму матричного расплава, подаче давления, необходимого для пропитки на зеркало расплава с помощью плунжера, выдержке до затвердевания матричного сплава и охлаждения формы. Дополнительное давление необходимо для обеспечения пропитки, т.к. промежутки между волокнами образуют капилляры. Обычно таким образом изготовляют локально армированные детали, что позволяет существенно улучшить их эксплуатационные свойства и сэкономить дорогостоящий наполнитель.

Сначала компрессионное литье использовали как способ улучшения качества нормированных отливок, но в начале 80-ых годов установили, что его можно использовать для изготовления отливок из КМ с алюминиевой матрицей. Экспериментально установлены следующие допустимые значения параметров технологического процесса:

Температура заливки - 650°-950° С Температура пресс- формы - 150— 315°С

Температура подогрева наполнителя - 300°- 1000° С

Давление пропитки -20-150 МПа

Время выдержки под давлением -30-120 секунд

Скорость прессующего поршня — от миллиметров до десятков миллиметров в секунду.

Теория пропитки армирующего каркаса расплавом строится на предположении о чисто гидродинамическом характере пропитывания, поэтому давление р_кр, обеспечивающее начало течения, определяется как сумма сопротивлений течению, а величина сопротивлению - по уравнению капиллярного противодействия в зазоре между элементами каркаса. Другими словами, между объемным содержанием и размерами частиц наполнителя с одной стороны, и величиной краевого угла смачивания, с другой. Для одномерного пучка волокон с плотной упаковкой

,

где σ – поверхностное натяжение, r_f -радиус волокна, V_f - объёмное содержание волокна.

Для описания самого процесса течения обычно используют уравнения, учитывающие гидродинамическое сопротивление в капиллярах. Тогда градиент давления вдоль потока Δp/Δz, обеспечивающий течение со скоростью u, будет для ламинарного режима:

где η- динамическая вязкость расплава

Поскольку с увеличением длины пропитанного слоя градиент давления уменьшается, скорость течения снижается, а длина пропитанного слоя изменяется во времени (τ) по параболическому закону:

l = кτ⁰_'⁵,

где к - константа пропитывания.

Расчеты, выполненные по рассмотренной теории для алюминиевой матрицы приводят к зависимости критического давления и длины пропитанного участка от времени, внешнего давления р ˃ р _кр, а также размера и содержания волокон, представлены на рисунке:

При объемных содержания волокон 0,5-0,6 критическое давление пропитки p_кр составляет 2-3МПа для углеродного волокна радиусом З мкм, для каркаса из борных волокон радиусом 50 мкм – 0,1 МПа. Константа пропитывания, определяющая длину пропитанного участка, возрастает с увеличением внешнего давления и снижается с увеличением объемной доли наполнителя.

Для V_f ⁼ 0,2-0,3 и внешних давлений больше 25 МПа каркасы довольно больших размеров пропитываются за несколько секунд.

Если пресс-форма и армирующий каркас нагреты недостаточно, то при пропитке расплав охлаждается, на поверхности наполнителя нарастает затвердевший слой металла и пропитываемость каркаса уменьшается. Это приводит к снижению скорости пропитывания и, соответственно, длины пропитанного участка. Вместе с тем слишком высокий нагрев наполнителя может привести к излишнему взаимодействию компонентов КМ, разупрочнению и охрупчиванию получающегося материала.

Величина давления в реальных процессах компрессионного литья определяется не режимом пропитки, а условиями подавления газовой пористости и достигает сотен атмосфер.

Следует отметить, что во всех рассматриваемых системах краевой угол смачивания превышает 110°, т.е. прочной адгезионной связи быть не должно. Однако связь между компонентами КМ получается достаточно прочной, что подтверждено исследованиями. Авторы большинства работ объясняют это взаимодействие волокон с легирующими элементами матриц. Вместе с тем в случае использования в качестве матрицы технического алюминия природа связи не ясна.

Метод компрессного литья может быть полезным при соединении элементов из КМ между собой.

элемент из КМ волокно пресс-форма матричный расплав плунжер

Согласно предложенному техническому решению, в соединяемых элементах стравливают матрицу, обнажая волокна на несколько мм. Затем элементы вкладывают в пресс-формы так, чтобы они впоследствии образовали деталь требуемой конфигурации, переплетают волокна в зоне соединения, заливают расплавом и прикладывают к нему давление. Расплав при пропитке соединяется с матричным сплавом элементов и образует в зоне соединения КМ того же или иного требуемого сплава.