3.4 Сравнительный анализ настроек пи-регулятора при различных методах расчета

После проведения расчета ПИ-регулятора тремя различными способами нужно выбрать оптимальные настройки, для этого сведем результаты расчетов в таблицу 3. Переходные процессы, полученные различными методами, представлены на рисунке 16.

Основному условию оптимальности соответствуют настройки регулятора, полученные методом РАФХ.

Таблица 5 Сравнительный анализ настроек ПИ-регулятора

Параметр сравнения	Метод расчета
	РАФХ	Циглера-Никольса	Инженерный
Коэффициент усиления	6,326	10,622	4,435
Время интегрирования , с	3,073	1,891	17,216
Степень колебательности	∞	∞	∞
Интегральный квадратичный критерий	0,259	0,155	12,486

Вывод: процессом, обеспечивающим минимум квадратичного критерия и обладающим степенью колебательности не ниже заданной ( ), является процесс, полученный при настройках регулятора, рассчитанных по методу Циглера-Никольса. Оптимальными настройками будут: и с.

Передаточная функция ПИ-регулятора будет иметь вид:

4 Параметрическая оптимизация системы с пид-регулятором

4.1 Метод расширенных амплитудно-фазовых характеристик

Передаточная функция ПИД-регулятора определяется по формуле:

(43)

где — коэффициент усиления регулятора;

— время интегрирования;

— время дифференцирования.

Расчетные формулы для настроек ПИД-регулятора:

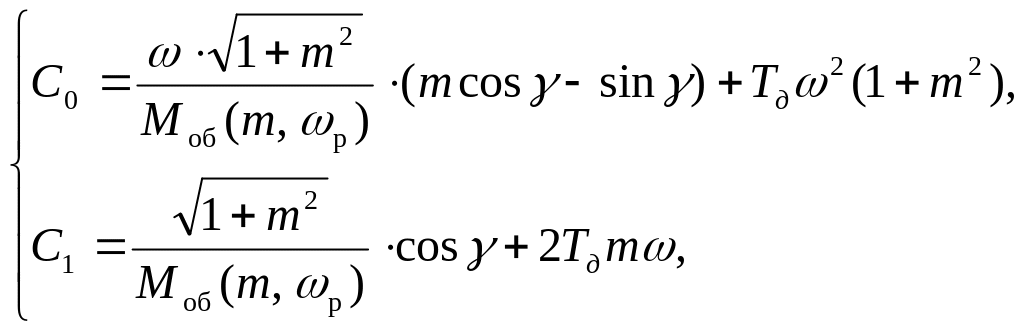(44)

где — коэффициент усиления регулятора, ;

— передаточный коэффициент интегральной составляющей, ;

— степень колебательности;

— расширенная амплитудно-частотная характеристика (РАЧХ) объекта , определяется по формуле;

; (45)

— расширенная фазо-частотная характеристика (РФЧХ) объекта (рисунок 8) определяется по формуле:

, (46)

где — рабочая частота.

Таким образом, мы имеем систему (44) двух уравнений с четырьмя неизвестными , , и . В связи с этим необходимо зафиксировать два параметра, после чего отыскивать решения. В расчете изначально фиксируется время дифференцирования ,где .

Для расчета оптимальных настроек регулятора зададимся рядом значений для С2:

С2₀ = 15, С2₁ = 30, С2₂ = 35,

На первом шаге выберем . В этом случае ПИД-регулятор является ПИ-регулятором, следовательно для него будут справедливы все настройки относящиеся к ПИ-регулятору за исключением дополнительного параметра-времени предварения.

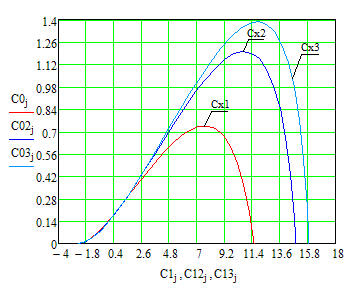
Рисунок 18 - Кривые равной колебательности

Программная реализация алгоритма в среде MathCAD представлена в приложении 8

Для дальнейшего расчета будем увеличивать значение до тех пор пока не добьемся получения оптимальных настроек. Результаты расчетов сведем в таблицу 6.

Таблица 6 Настройки ПИД-регулятора

Параметр сравнения	Сx1	Cx2	Cx3
	15	30	35
Коэффициент усиления	9,95	13,076	14,35
Время интегрирования , с	1,801	1,013	0,906
Степень колебательности	0,392	∞	∞
Интегральный квадратичный критерий	0,108	0,064	0,059
Рабочая частота	0,195	0,22	0,232

Проведя сравнительный анализ всех настроек, можно сделать вывод о том, что наиболее оптимальными являются настройки соответствующие времени дифференцирования равному 35 с, , так как при полученных настройках получается процесс, обеспечивающий минимум квадратичного критерия и обладающий степенью колебательности не ниже заданной m=0.29.

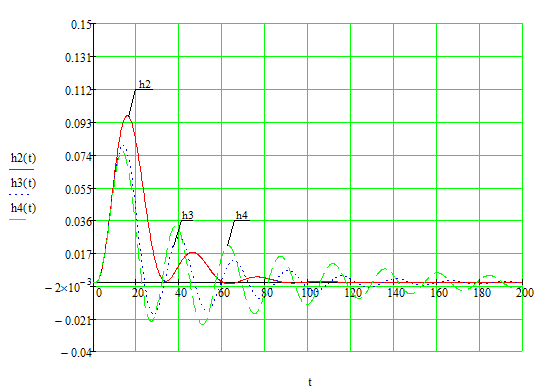
Рисунок 19 – Сравнение переходных характеристик замкнутой системы при различныхоптимальных настройках

Программная реализация алгоритма в среде MathCAD представлена в приложении 6