3.2 Параметрическая оптимизация методом незатухающих колебаний (метод Циглера-Никольса)

Данный метод является приближенным методом расчета оптимальных настроек/

Расчет идет из основного уравнения:

(29)

где

(30)

Из (29) получаем:

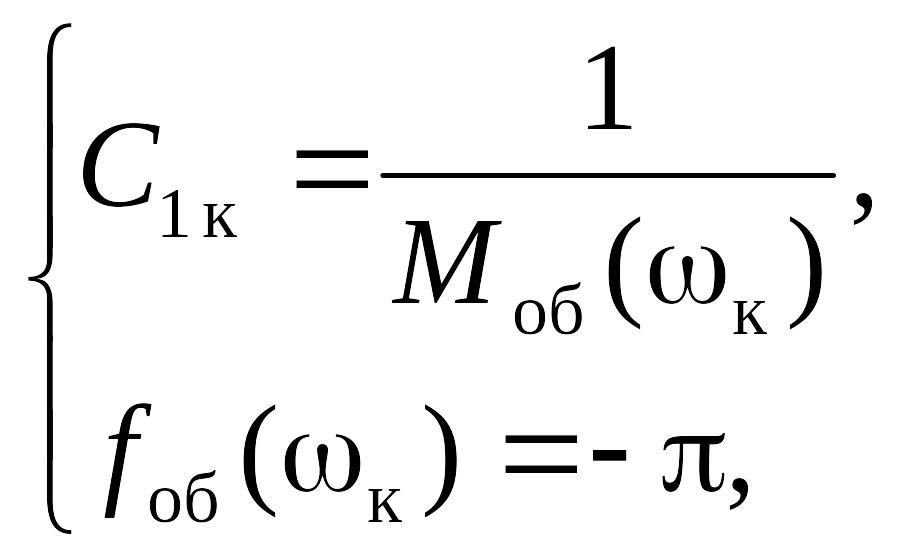(31)

где — критическая частота, соответствующая предельным настройкам П-регулятора.

— фазо-частотная характеристика (ФЧХ) объекта (рисунок 11):

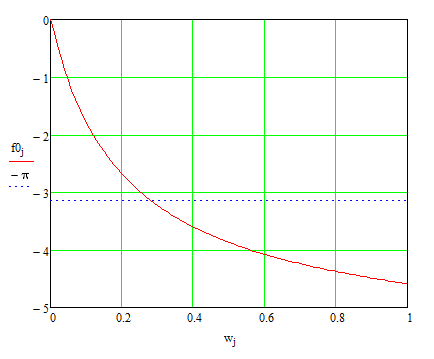
Рисунок 12 - Фазо-частотная характеристика объекта

Решая второе уравнение системы (31), находим, что

(32)

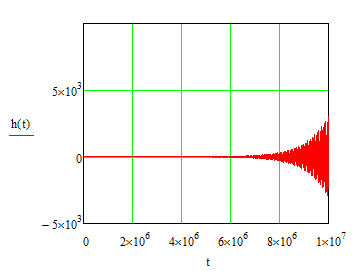
Рисунок 13 – Переходная характеристика замкнутой АСР с П-регулятором

Также для проверки правильности найденного значения построим АФХ разомкнутой системы.

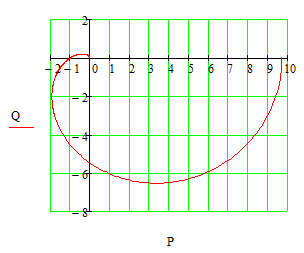
Рисунок 14 - Амплитудо – фазовая характеристика разомкнутой системы

Затем, подставив выражение (32) в первое уравнение системы (31), находим:

Рабочие настройки ПИ-регулятора определяются по следующим формулам Циглера-Никольса [2]:

(33)

Тогда параметры ПИ-регулятора будут определяться как:

1. коэффициент усиления:

2. время интегрирования:

3. время изодрома:

Подставив полученные настройки в (16), получим передаточную функцию ПИ-регулятора:

Передаточная функция замкнутой системы с ПИ-регулятором определяется как:

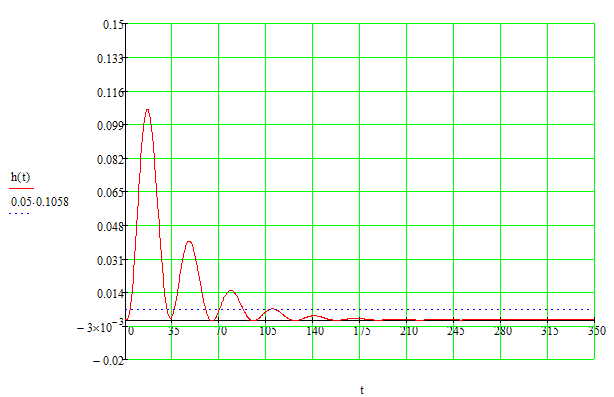
Рисунок 15 - Переходный процесс замкнутой системы

Определим параметры качества переходного процесса:

1. время регулирования:

2. интегральный квадратичный критерий:

(34)

3.3 Параметрическая оптимизация инженерным методом

В практике наладочных работ широко используют приближённые формулы для определения оптимальных параметров настройки регулятора в зависимости от параметров моделей объектов управления и различных критериев оптимальности.

Наиболее длительную проверку временем выдержали формулы (таблица 7.13 [4]), опубликованные Всесоюзным теплотехническим институтом им. Ф.Э. Дзержинского (ВТИ). В качестве критерия параметрической оптимизации в формулах ВТИ приняты степень затухания и интегральная квадратичная оценка качества , близкая к минимуму.

Выбор формул ВТИ основан на определении коэффициента усиления объекта управления и вычислении отношения

(38)

где — транспортное запаздывание объекта управления;

— постоянная времени объекта управления.

В данном методе необходимо построить переходную характеристику объекта управления (рисунок 14). Для этого нужно произвести обратное преобразование Лапласа передаточной функции объекта управления.

(39)

Коэффициент усиления объекта управления:

(40)

Для определения и нужно построить касательную к переходной характеристике в точке перегиба (рисунок 14).

Для нахождения точки перегиба нужно решить уравнение:

Рисунок 16 - Переходная характеристика объекта управления

и .

Так как отношение, то имеют место формулы:

(41)

Тогда остальные настройки ПИ-регулятора будут определяться как:

1. коэффициент усиления:

2. время интегрирования:

Подставив полученные настройки в (16), получим передаточную функцию ПИ-регулятора:

Передаточная функция замкнутой системы с ПИ-регулятором определяется как:

Из передаточной функции путем обратного преобразования Лапласа получаем переходный процесс.

Определим параметры качества переходного процесса:

1. интегральный квадратичный критерий:

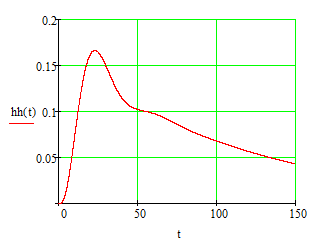
Рисунок 17 - Переходный процесс замкнутой системы

Программная реализация алгоритма в среде MathCAD представлена в приложении 5