Содержание:

1 Анализ технологического процесса как объекта управления 5

2 Получение передаточной функции объекта управления 7

3 Параметрическая оптимизация системы с ПИ-регулятором 14

3.1 Метод расширенных амплитудно-фазовых характеристик 14

3.2 Параметрическая оптимизация методом незатухающих колебаний (метод Циглера-Никольса) 19

3.3 Параметрическая оптимизация инженерным методом 22

3.4 Сравнительный анализ настроек ПИ-регулятора при различных методах расчета 24

4 Параметрическая оптимизация системы с ПИД-регулятором 25

4.1 Метод расширенных амплитудно-фазовых характеристик 25

4.2 Параметрическая оптимизация методом незатухающих колебаний (метод Циглера-Никольса) 28

4.3 Параметрическая оптимизация инженерным методом 29

4.4 Сравнительный анализ настроек ПИД-регулятора при различных методах расчета 32

5 Анализ полученных результатов 33

6 Список литературы 35

1 Анализ технологического процесса как объекта управления

Технологический процесс реализуется с помощью двух объектов и регулятора. Объекты соединены последовательно и объединены с регулятором по принципу отрицательной обратной связи.

В данном технологическом процессе происходит нагрев жидкости от некоторой начальной температуры до требуемой выходной температуры продукта. Жидкость с расходом при температуре поступает в емкость. В емкосте она подогревается до температуры при помощи ТЭНа. Напряжение на ТЭНе регулируется реохордом. Пройдя через емкость, жидкость поступает в теплообменник, в котором нагревается до требуемой выходной температуры с допустимым отклонением .

Входным параметром емкости является уровень жидкости, а выходным — расход жидкости. Кроме этого емкость испытывает возмущающее воздействие в виде колебаний расхода жидкости в емкости.

Рисунок 2 - Структурная схема объекта управления: X — входная величина; Y — выходная величина; Z — возмущение; — передаточная функция теплообменника; — передаточная функция емкости;

Входным параметром теплообменника является расход жидкости, а выходным температура продукта на выходе. Продукт в теплообменнике подогревается горячим теплоносителем. Температура продукта на выходе теплообменника зависит от температуры греющего агента и исходного продукта на входе, а также от расхода агента и продукта.

Входным параметром регулятора является рассогласование, то есть разница между действительной температурой продукта и заданной, а выходным — управляющее воздействие. Расход изменяется регулирующим органом под действием сигналов поступающих от регулятора.

Структурная схема контура управления представлена на рисунке 3.

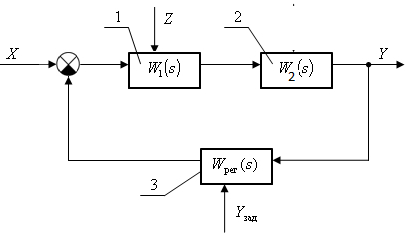
Рисунок 3 - Структурная схема контура регулирования:

1 — теплообменник; 2 — емкость; 3 — регулятор; X — входная величина; Y — выходная величина; Z — возмущение — сигнал задания; — передаточная функция емкости;

— передаточная функция теплообменника; — передаточная функция регулятора.

Передаточная функция замкнутой системы с ПИ-регулятором будет выглядеть следующим образом:

.

2 Получение передаточной функции объекта управления

По табличным данным (таблица 2) построим кривую разгона (рисунок 4).

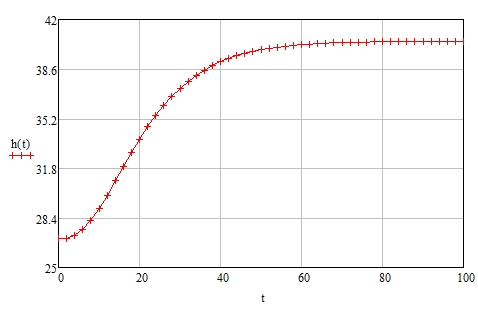
Рисунок 4 – Кривая разгона

Для того чтобы найти передаточную функцию теплообменника нужно аппроксимировать кривую разгона. Для этого необходимо привести ее к единичному ступенчатому воздействию:

(

где — текущее значение кривой разгона;

— начальное значение кривой разгона (вводится для приведения переходной характеристики к нулю). ;

, — минимальное и максимальное значение диапазона изменения температуры соответственно. , ;

A — амплитуда входного ступенчатого воздействия, выраженная в долях.

Амплитуда входного ступенчатого воздействия:

(

где — изменение расхода;

, — минимальное и максимальное значение диапазона изменения расхода соответственно. , .

Определим изменение расхода:

. (

Тогда амплитуда по формуле (2) будет равна:

.

Переходная характеристика по формуле (1) будет связана с кривой разгона соотношением:

_.

Построим переходную характеристику, используя соотношение (1) (рисунок 5).

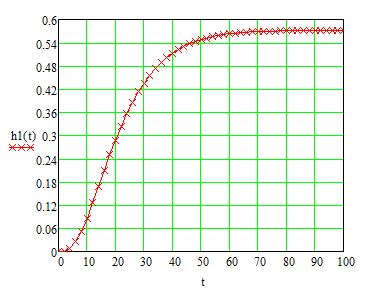
Рисунок 5 – Переходная характеристика

Аппроксимировать данную переходную характеристику будем по методу «трех точек».

При аппроксимации переходной характеристики представим теплообменник звеном, состоящим из двух последовательно соединенных апериодических звеньев первого порядка. Таким образом, передаточную функцию теплообменника будем искать в виде:

(4)

где k — коэффициент усиления объекта;

, — постоянные времени апериодических звеньев.

Критерием приближения в «методе трех точек» является требование совпадения аппроксимируемой h1(t) и аппроксимирующей h2(t) характеристик в точках t = 0, t =  и в точке перегиба t_П.

Кроме того, в точке перегиба эти характеристики должны иметь одинаковый наклон . Таким образом, критерий приближения имеет следующий вид:

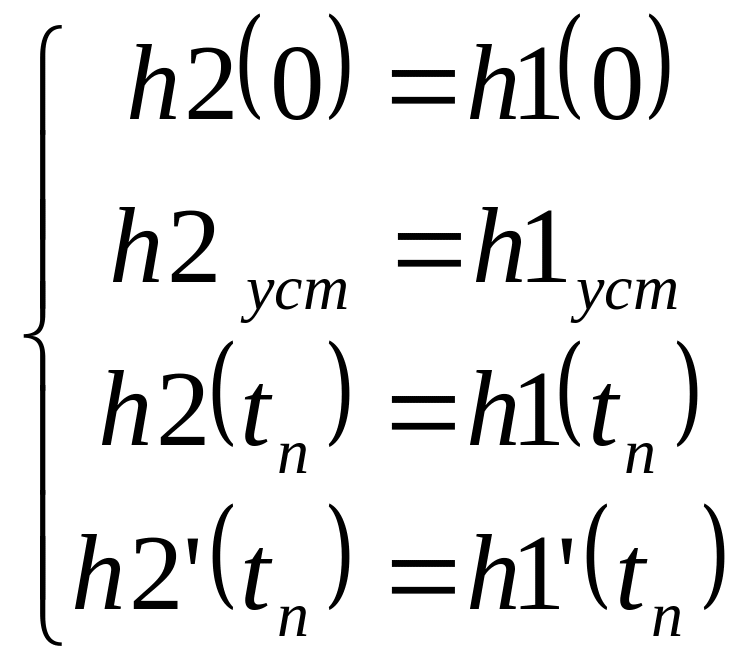
Для определения коэффициентов передаточной функции (k, Т_О, _О) на графике переходной характеристики проводят касательную в точке перегиба (рисунок 6).

Рисунок 6 - Касательная в точке перегиба переходной характеристики

Коэффициент усиления объекта определяется как , т.е. k=h_УСТ, где h_УСТ - новое установившееся значение выходной величины. Постоянная времени T_О определяется наклоном касательной и равна отрезку, отсекаемому ею при пересечении с осью абсцисс (старое равновесное состояние) и с прямой, определяющей уровень нового установившегося значения выходной величины. Отрезок же от начала координат до точки пересечения касательной с осью абсцисс равен времени транспортного запаздывания _О.

Определяем коэффициент усиления объекта. В качестве установившегося значения переходной характеристики примем максимальное значение переходной характеристики:

(6)

Для определения постоянных времени и необходимо воспользоваться номограммой (рисунок 8):

• рассчитываем коэффициент b, используя переходную характеристику:

(7)

• на оси b отложим полученное значение и проведем горизонтальную прямую до пересечения с жирной линией (b) с обозначением n=1 и отмечаем точку пересечения;

• проведем вертикальную прямую и считаем по горизонтальной шкале значение соотношения Т₂/Т₁, а также отметим точки пересечения с кривыми (Т₁/Т₀) и (t_П.А./Т₁) для n=1;

• от точек пересечения проведем горизонтальные прямые и считаем по соответствующим шкалам величины соотношений Т₁/Т₀ и t_П.А./Т₁;

• по графику переходной характеристики (рисунок 6) определить параметр Т₀ и рассчитать из соотношений t_П.А. ,Т₁ ,Т₂ .

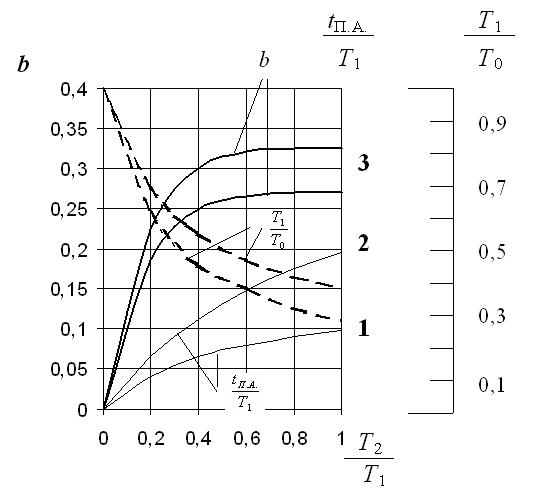
Рисунок 7 - Номограмма для определения отношений T₁/T_o, T₂/T₁, t_П.А./T₁.

(8)

(9)

(10)

(11)

(12)

(13)

;

;

.

После проверки совпадения по трем точкам и уточнения параметров имеем:

Зная значения всех необходимых параметров, находим выражение для аппроксимирующей переходной характеристики h2(t) по следующей формуле:

, (14)

где — знак операции «обратное преобразование Лапласа».

Построим в одной графической плоскости графики аппроксимируемой h1(t) и аппроксимирующей ha(t) функций (рисунок 8).

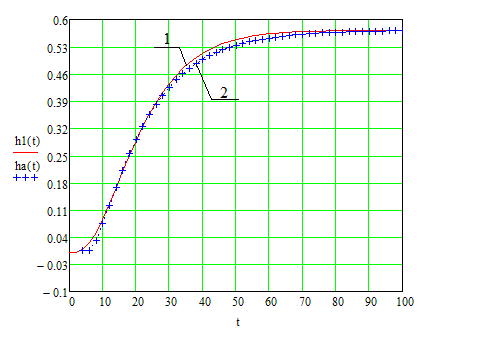
Рисунок 8 - Графики аппроксимируемой h1 и аппроксимирующей ha функций

1-аппроксимируемый h1, 2-аппроксимирующий ha

Определим ошибку аппроксимации

, (15)

Площадь под аппроксимированной переходной характеристикой

,

. (16)

Площадь под экспериментальной переходной характеристикой

(17)

.

Подставляя (16) и (17) в выражение (15), получаем

.

Ошибка аппроксимации переходной характеристики объекта с самовыравниванием по "трем точкам" более 1%, что не удовлетворяет условию, но при изменении параметров соблюдение условия совпадения в трех точках нарушится. Т.о. данная точность будет оптимальной и минимальной.

Окончательно получаем, что передаточная функция теплообменника имеет вид:

Передаточная функция объекта согласно схеме (рисунок 3) будет иметь вид:

Программная реализация алгоритма в среде MathCAD представлена в приложении 1.