4.2.2. Основная модель управления запасами (определение оптимального размера заказа)
ПОСТАНОВКА ЗАДАЧИ определить размер заказа, при котором затраты, связанные с оборотом запасов сырья и материалов, будут минимальны.
ПРЕДПОЛОЖЕНИЯ ДЛЯ МОДЕЛИ
• Потребность в запасах постоянна и определенна
• Цены на запасы не изменяются значительно
• Время поставки равно нулю
• Отсутствие запасов на складе не допустимо
• Весь объем заказа поставляется одновременно
• Заказы на разные виды запасов осуществляются независимо друг от друга
О
птимальный
размер заказа (ОРЗ) – это такой объем
покупки, при котором суммарные затраты
на хранение и выполнение заказов
минимальны (рис.1.3).
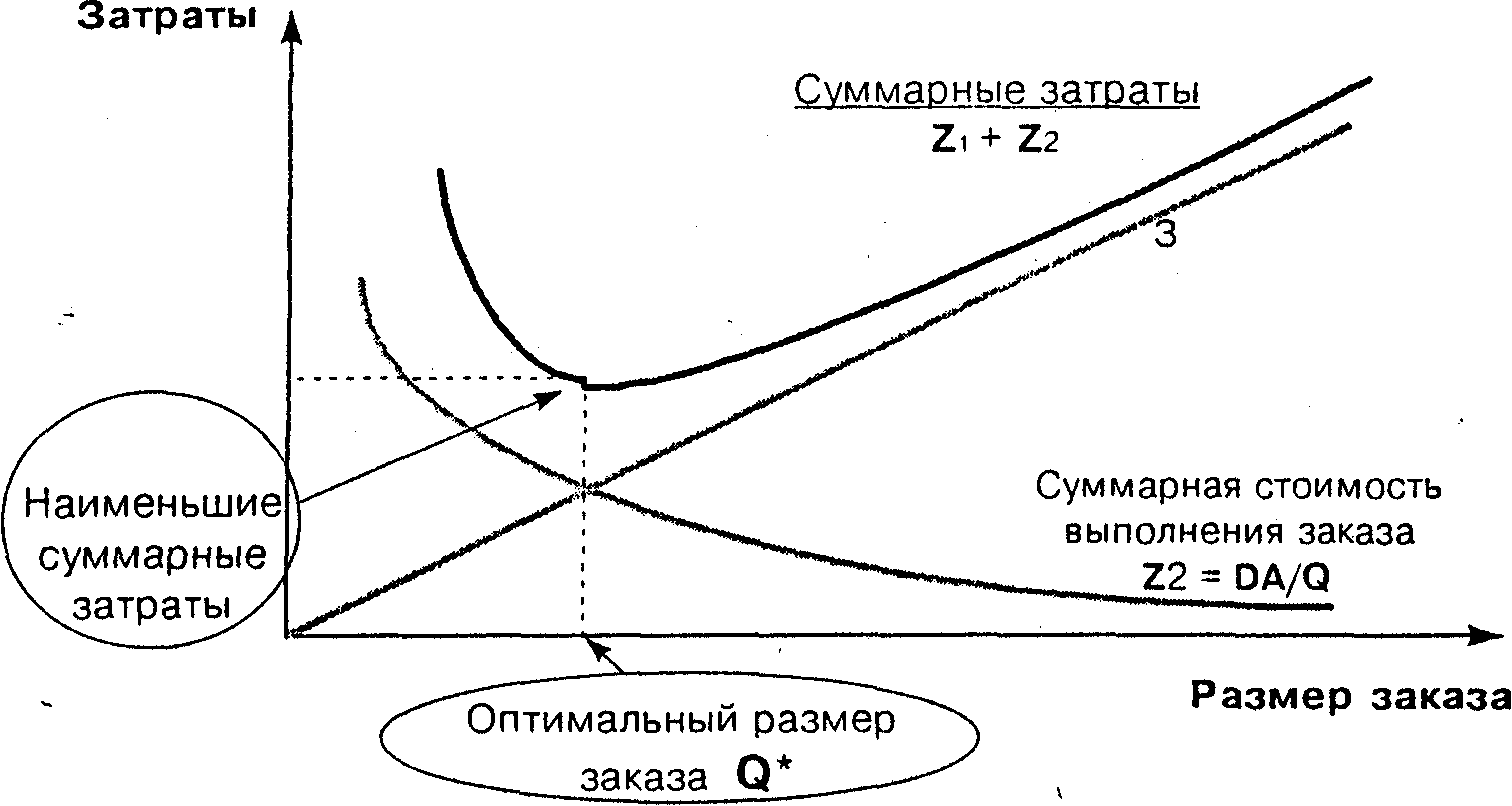
Рис. 1.3. Определение оптимальной партии заказа
Суммарные затраты минимальны тогда, когда затраты на хранение равны затратам на выполнение заказов:
,
(1.5)
Из уравнения (1.5) определяем оптимальный размер заказа и совокупные расходы на заказ:
(ОРЗ)=
=
,
(1.6)
TC=
(1.7)
•При уменьшении стоимости выполнения заказа (Col) OP3 уменьшается, а частота выполнения заказов увеличивается.
•При увеличении стоимости хранения (Ch) OP3 уменьшается, следовательно, необходимо снизить средний объем запасов на складе.
•Увеличение потребности в запасах (D) приводит к увеличению OP3.
ОПТИМАЛЬНЫЙ РАЗМЕР ЗАКАЗА (время поставки не равно нулю)
При ненулевом времени поставки возникает проблема - когда размещать заказ для того, чтобы избежать отсутствия запасов на складе.
ТОЧКА ПЕРЕЗАКАЗА - уровень запасов на складе, при котором заказывается новая партия товара - равна потребности за время поставки.
Если для получения заказанной партии продукции необходимо время поставки Тп дней, а Тц - цикл потребления запасов, то заказ следует размещать в момент времени Тц - Тп. С другой стороны, для удовлетворения спроса за время поставки необходим запас продукции в размере (D/365)*Тп. В этом случае закачанная партия будет получена в момент, когда запасы исчерпаются (рис.1.4).
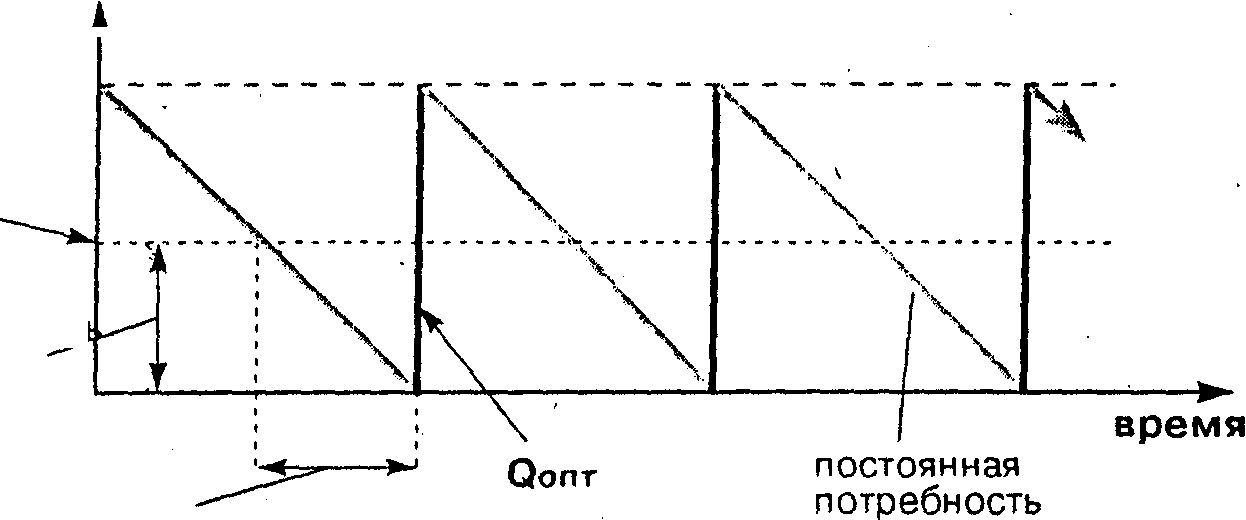
Рис. 1.4. Динамика запасов без учета страхового запаса
Пример: ОПТИМАЛЬНЫЙ РАЗМЕР ЗАКАЗА (пример расчета и анализ чувствительности), используем формулу (1.7)
Рассчитаем (ОРЗ) для следующих условий:
Годовая потребность (D) |
10000шт. |
Стоимость выполнения 1 заказа (Col) |
50 000 руб. |
Стоимость покупки единицы запасов (Р) |
50 000 руб. |
Стоимость хранения 1 руб. запасов за год (Ch) |
0,5 (50%) |
Количество заказов в год = 10000/200 =50.
Р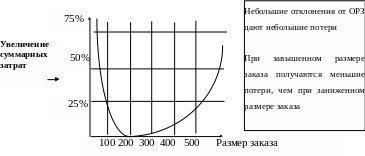
ассмотрим
динамику роста суммарных затрат по
приобретению и хранению запасов в
зависимости от размера заказа (рис.1.5).
Рис. 1.5. Зависимость суммарных затрат от размера заказа.
ОПТИМАЛЬНЫЙ РАЗМЕР ЗАКАЗА (принятие решения при скидке)
Постановка задачи. Поставщик сырья предлагает вам скидку на закупаемый товар с условием, что объем одного заказа будет больше какой-то величины. Всегда ли выгодно принимать предложение поставщика о скидке с таким условием? Для решения данной задачи необходимо найти такой размер заказа, при котором суммарные затраты, с учетом закупочной стоимости, будут минимальны, причем размер этого заказа не обязательно должен быть равен оптимальному размеру заказа.
Введем дополнительные обозначения:
Qb - минимальный возможный размер заказа при скидке; d - размер скидки (например: d=0.l - скидка 10%)
ТС - суммарные затраты, включающие в себя затраты на хранение, затраты на выполнение заказов и суммарные переменные затраты.
Если цена единицы продукции постоянна, то на уровень оптимального заказа она влияния не оказывает. Другое дело, если на большие партии продукции поставщик устанавливает скидку. Тогда кривая общей стоимости запасов, включая цену покупки, будет смещаться, как показано на рис. 1.6, б.
Если минимум кривой не включается в интервал скидки, то эта точка уже не является оптимальным размером заказа. Чтобы найти оптимальный размер заказа, необходимо пересчитать общие затраты на запасы, включая цену продукции для начального значения количества ql, q2 каждого из интервалов скидки, и выбрать наименьшие (рис. 1.6, а).
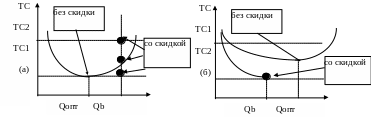
Рис. 1.6. Зависимость суммарных затрат от размера заказа
Алгоритм решения:
Шаг1. Рассчитать оптимальный размер заказа Qîïò(d) при наличии скидки.
Шаг2. Сравнить Qopt(d) и Qb. Если Qopt(d) >= Qb, тогда предложение поставщика выгодно и Qopt(d) самый выгодный размер заказа.
Если Qopt(d) < Qb, то переходим к шагу 3.
ШагЗ. Вычислить суммарные затраты для ОРЗ без учета скидки по формуле:
,
(1.8)
где Р – стоимость покупки единицы запасов.
Вычислить суммарные затраты для минимального возможного размера заказа с учетом скидки.
(1.9)
Если ТС1 < TC2 тогда предложение по скидке невыгодно.
Если ТС1 > TC2 тогда предложение по скидке выгодно и оптимальный размер заказа равен Qb.
Данный алгоритм можно легко логически расширить для случая, когда вам предлагают несколько вариантов скидок с различными граничными условиями, важно помнить, что наиболее выгодный размер заказа будет равен или одному из оптимальных размеров заказов или одному из граничных условий.
ОПТИМАЛЬНЫЙ РАЗМЕР ЗАКАЗА (принятие решения при увеличении цены )
Постановка задачи: Вы узнали, что цена на комплектующие, которые вы закупаете завтра, возрастет. Сегодня вы делаете закупку этих комплектующих и перед, вами стоит задача: каков должен быть эффективный размер сегодняшнего заказа Qэф для того, чтобы найти оптимальное соотношение между возросшими затратами на хранение и экономией в связи с повышением цены (рис.1.7)?
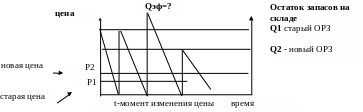
Рис. 1.7. Определение оптимального размера заказа при увеличении цены
АЛГОРИТМ РЕШЕНИЯ:
• Затраты на хранение каждой дополнительной единицы в заказе будут увеличиваться, так как возрастает время, которое она пролежит на складе (мы предполагаем, что потребность в запасах не изменяется).
• Период времени, который дополнительная единица будет находиться на складе, равен t=Q/D, где Q - размер заказа; D - потребность в запасах.
• Затраты на хранение дополнительной единицы Chl(t) определяются по формуле:
, (1.10)
где Сh1 – затраты на хранение единицы запасов по старой цене.
• Размер заказа мы будем увеличивать до тек пор, пока затраты на хранение Chl(t) äëÿ дополнительной единицы не превысят увеличение цены.
Уравнение (1.10) характеризует предел, до которого выгодно увеличивать размер заказа.
Для Q+1-ой единицы заказа затраты на хранение превысят экономию, связанную с покупкой единицы по старой, более низкой цене.
• Если Qэф < Qопт, тогда размер заказа равен Qопт.
Qэф
,
(1.11)
где Qэф. – эффективный размер заказа при повышении цены.
ОПТИМАЛЬНЫЙ РАЗМЕР ЗАКАЗА (комбинированный заказ)
Постановка задачи: Часто бывает, что мы покупаем у одного и того же поставщика несколько наименований товара. Как правило, если мы заказываем одновременно несколько наименований, мы имеем экономию затрат на выполнение заказов, так как в один заказ включаем несколько элементов. Как рассчитать при этом оптимальные размеры заказов и частоту их возобновления. Выгодно ли комбинировать заказы или лучше заказывать все материалы отдельно.
Оптимальная частота заказов (Nопт) при комбинированном заказе определяется по формуле:
(1.12)
Планируемый объем отгрузки в рублях «V» по себестоимости равен:
,
(1.13)
Для нескольких наименований объем отгрузки в рублях по себестоимости будет равен:
,
(1.14)
Таким образом, рассчитав D*P для нескольких наименований и определив стоимость выполнения комбинированного заказа (А), мы можем рассчитать (Nопт) – оптимальную частоту заказа. Зная Nопт, мы можем рассчитать оптимальный размер заказа для каждого наименования заказываемого товара по следующей формуле:
Q1=D1/Nопт; Q2=D2/Nопт; Q3=D3/Nопт и т.д., (1.15)
Для определения эффективности комбинированного заказа необходимо сравнить суммарные затраты для комбинированного заказа и для независимых заказов при оптимальных размерах заказов.