9.8 Ізокліни. Побудова інтегральних кривих за допомогою ізоклін

При побудові фазових траєкторій процесів, які описують диференціальні рівняння другого порядку, зручно користуватися методом ізоклін. Під ізокліной (лінією рівного нахилу) розуміють геометричне місце точок фазової площини, для яких похідна є деяке постійне число. Для однієї ізокліни, наприклад, для іншої і т.д. Значення похідної дорівнює кутовому коефіцієнту дотичної, що проведена до будь-якої інтегральної кривої в точці її перетину з ізокліною, для якої

Виведемо рівняння для побудови сімейства ізоклін для коливального LС - контуру, що підключається до джерела напруги U (див. приклад 9.2). Диференціальне рівняння, що описує роботу цього лінійного кола, має вид:

. (9.1)

Введемо позначення: i(t)=x(t); відповідно Враховуючи, що одержуємо

(9.2)

Розвязуємо (9.2) відносно „у” і одержуємо рівняння для побудови сімейства ізоклін:

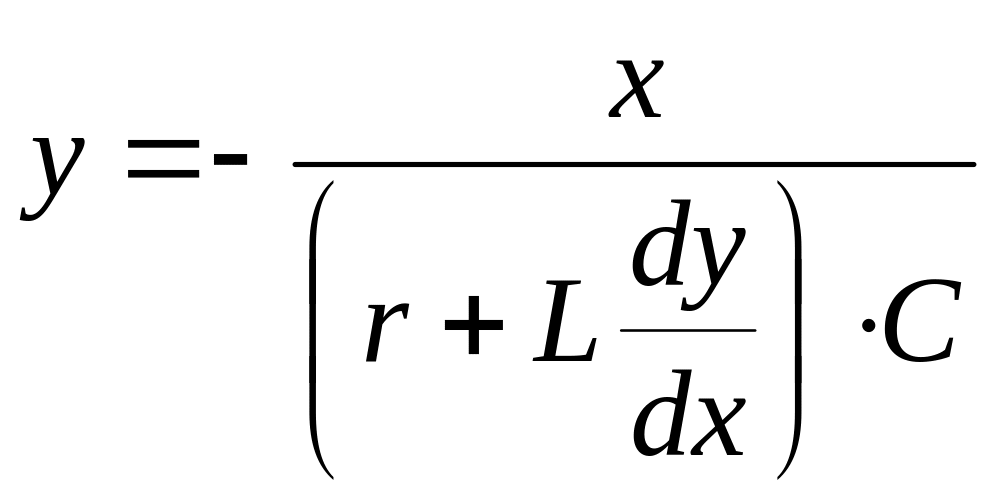. (9.3)

Для визнічення точок фазової площини, що належать першій ізокліні, в рівнянні (9.3) підставляють k₁ замість . Надають „x” різні значення і з рівняння (9.3) одержують при відповідні значення „у”. Сукупність визначених точок дає ізокліну, для якої . Потім приймають і у такий же спосіб будують другу ізокліну і т.д. При графічному зображенні ізоклін на них наносять риски (зарубки), що відображають відповідні кути, які дотичні утворюють з віссю ОХ.

Для лінійних кіл ізокліни є прямі лінії, що проходять через початок координат. Для нелінійних кіл - в загальному випадку непрямі лінії.

Після побудови сімейства ізоклін на фазовій площині можна побудувати інтегральні криві. Припустимо, що треба побудувати інтегральну криву [тобто залежність у =f(x)], яка проходить через т.А, що належить ізокліні 1 (див. рис. 9.6).

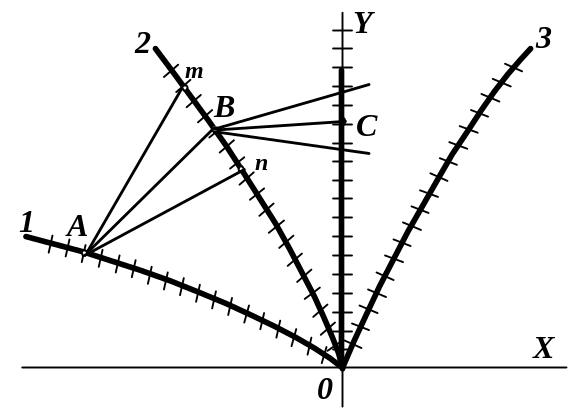
Рисунок 9.6 – До побудови інтегральних кривих методом ізоклін

Один з варіантів побудови наступний:

- з т. А проводять два відрізки до перетину з ізокліною 2; причому, перший відрізок проводять так, щоб він складав з віссю ОХ, кут, тангенс якого дорівнює (кутовому коефіцієнту ізокліни 1) – тобто співпадав за напрямком з зарубками ізокліни 1; хай цей відрізок перетинає ізокліну 2 в точці „m”; другий відрізок проводять під кутом, що відповідає зарубкам ізокліни 2; хай він перетинає ізокліну 2 в точці „n”;

- ділять відстань між т. m і n навпіл і одержують т. B; сполучають т. А і B відрізком прямої – це і є шматочок інтегральної кривої;

- далі проводять два відрізки з т. B до перетину з наступною ізокліною (на рис 9.2 це вісь OY) і одержують т. С. Відрізок BC є новим шматочком інтегральної кривої. І т.д. Чим ближче будуть розташовані ізокліни одна до одної, тим краще, точніше ламана лінія відповідатиме інтегральній кривій.

Для нелінійних кіл сімейство ізоклін часто будують, замінюючи характеристику нелінійного елементу відрізками прямих ліній. В цьому випадку для кожної лінійної ділянки апроксимуючої характеристики нелінійного елементу на фазовій площині будують своє сімейство ізоклін. Кожне з них відповідає тільки певній області зміни x, межа якої визначається з характеристики нелінійного елементу.

9.9 Стійкий і нестійкий граничні цикли

Якщо процес в електронному (електричному) колі є періодичним, то фазова траєкторія має вид замкнутої кривої. Замкнута фазова траєкторія називається граничним циклом. Стійким граничним циклом називають такий, до якого наближаються (навиваються) розташовані всередині і поза ним довколишні інтегральні криві. Фізично він відповідає сталому періодичному процесу (лінія 2 на рис. 7.7). Нестійким називається граничний цикл, від якого віддаляються (розкручуються) поблизу розташовані інтегральні криві (лінія 1 на рис. 9.7).

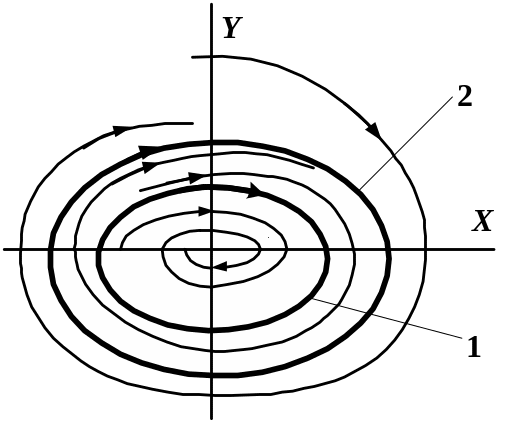
Рисунок 9.7 – Зображення граничних циклів на фазовій площині

(1 – нестійкий граничний цикл; 2 – стійкий граничний цикл)

9.10 Побудова осцилограм сигналів за відомим фазовим зображенням

Хай динамічні процеси в нелінійному колі описує наступне нелінійне рівняння другого порядку:

(9.4)

де u(t) – миттєве значення напруги на якій-небудь гілці кола, нелінійні коефіцієнти, що залежать від u(t).

Для побудови фазового зображення введемо позначення: u(t)= x(t); відповідно du/dt=dx/dt = y(t), d²u/dt² = y∙(dy/dx). Тоді рівняння (7.4) можна записати так:

звідки рівняння ізокліни матиме вигляд:

(9.5)

де - кутовий коефіцієнт i-ї ізокліни.

Хай з використанням (9.5) побудовано сімейство ізоклін, а за допомогою ізоклін побудована на фазовій площині фазова траєкторії кола y=f(x, t) - рис. 9.8. Рівняння відрізка траєкторії замкнутого циклу, що зображений суцільною лінією на рис. 9.6, можна записати у вигляді y= bx + c для х₁ ≤ х ≤ х₂. Оскільки у=dx/dt, це рівняння можна переписати у такий спосіб:

Виконуємо інтегрування останнього рівняння:

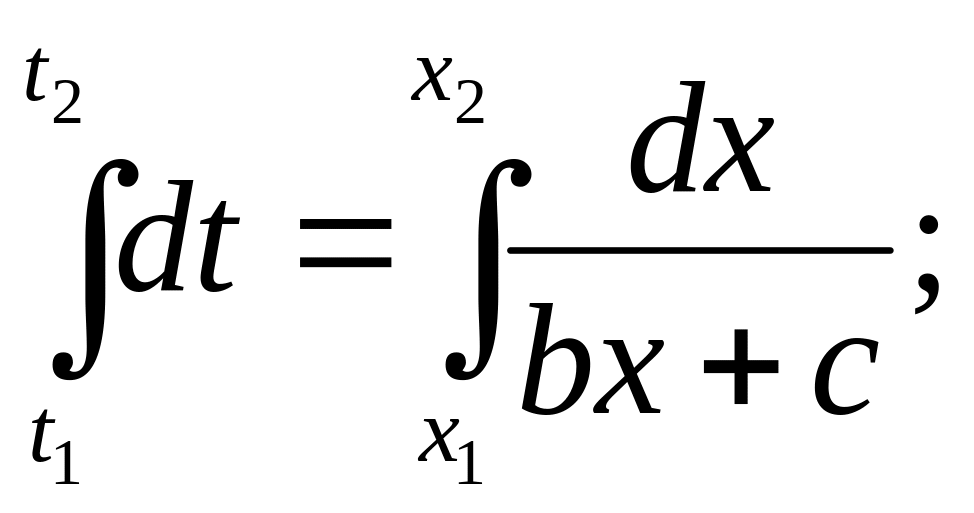
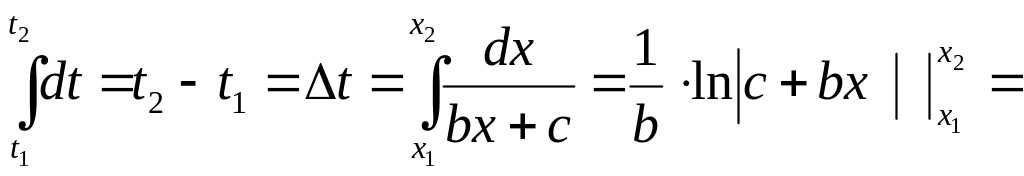
З останнього виразу видно, що „x” на фазовій траєкторії змінюється від значення х₁ до значення х₂ за час Δt, причому:

Таким чином, якщо визначити час Δt_i для кожного i-го відрізка фазової траєкторії досліджуваного кола (рис. 9.8), можна побудувати графік зміни в часі напруги u(t), тобто осцилограму сигналу u(t).

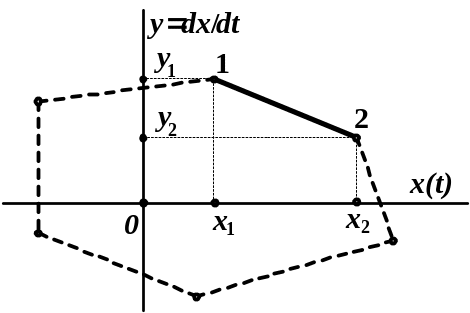
Рисунок 9.8 – До побудови осцилограм сигналів за

відомим фазовим зображенням процесу

9.11 Якісне дослідження процесів у нелінійних колах за допомогою

фазової площини

Побудови на фазовій площині можуть проводитися з метою дослідження:

а) стійкості стану рівноваги;

б) можливості виникнення в схемі автоколивань;

в) визначення амплітуди автоколивань;

г) впливу п.у. на процеси, що мають місце вколі, і т. п.

Припустимо, що для деякого кола для миттєвих значень струму або напруги побудовані інтегральні криві, що відповідають зображеним на рис. 7.7. Які ж висновки можна зробити відносно можливих перехідних процесів в цьому колі при тому значенні параметрів кола, для яких ці криві побудовані? Відповідь наступна:

- в колі можливий лише один стійкий стан рівноваги, що відповідає початку координат;

- на фазовій площині є лише один стійкий граничний цикл (2) і один нестійкий цикл (2);

- якщо початкові умови в колі такі, що зображаюча точка, що характеризує ці умови, потрапляє всередину нестійкого граничного циклу (кривої 1), то в системі виникає коливальний процес, що затухає, і в результаті якого коло прийде з часом в стан стійкої рівноваги;

- якщо ж початкові умови такі, що зображаюча точка потрапляє в область, яка знаходиться зовні кривої 1, то в підсумку перехідного процесу в колі виникнуть стійкі автоколивання і зображаюча точка рухатиметься по стійкому граничному циклу – по кривій 2.

Таким чином, можна говорити, що в колі буде або стійкий "в малому" стан рівноваги, або буде стійкий автоколивальний процес. Який з цих режимів виникає в колі, все залежить від початкових умов.

За допомогою фазової площини при дослідженні нелінійних систем (кіл), що знаходяться під впливом періодичної збурюючої сили, можна вирішити наступні питання:

- дослідити вплив початкових умов на характер сталого або квазісталого процесу;

- дослідити стійкість субгармонійних* коливань і резонансів на вищих гармоніках;

- дослідити стійкість процесів автомодуляції (у цьому випадку побудови на фазовій площині роблять для величин, що зміняються поволі, або для огинаючих амплітуд).

^* Під субгармонійними розуміють коливання, частота яких менше частоти періодичної діючої на систему сили, що вимушує.