9 Динамічний аналіз нелінійних електронних
схем в часовій області
9.1 Загальна характеристика аналізу перехідних процесів в нелінійних колах
Перехідні процеси в нелінійних колах істотно відрізняються від перехідних процесів в лінійних колах. Нелінійність характеристики будь-якого елементу кола може привести і до чисто кількісної зміни характеристик перехідного процесу, і до появи нових явищ. У першому випадку нелінійність кола може збільшити швидкість перехідного процесу на одному проміжку часу, зменшити швидкість в іншому проміжку; при цьому може зрости максимальне значення струму в перехідному режимі, проте якісна сторона процесу залишається без істотних змін. У другому випадку за рахунок нелінійності виникають нові явища, принципово неможливі в лінійному колі:
а) у лінійному колі включення джерела постійної або гармонійної е.р.с. (або струму) супроводжується деяким затухаючим перехідним процесом, який з часом переходить в примушений режим, частота якого дорівнює частоті джерела; у нелінійному колі перехідний процес може привести до виникнення коливань з частотою, відмінною від частоти сигналу джерела (автоколивань);
б) у лінійному колі напруги і струми в перехідному процесі звичайно можна представити у вигляді суми двох складових: вільної і примушеної; у аналізі нелінійного кола принцип суперпозиції непридатний і не можна розкладати струми і напруги на вільні і примушені складові.
Аналіз перехідного процесу в лінійному колі найчастіше зводитися до рішення системи лінійних диференціальних або алгебраічних рівнянь з постійними коефіцієнтами. Вони є найпростішими. Математичний апарат рішення таких рівнянь розроблений достатньо повно і задача аналізу зводитися, як правило, до знаходження найбільш економічного і наочного методу інженерного розрахунку. При аналізі лінійних кіл широко застосовуються принципи суперпозиції і взаємності.
Значно складніша справа з розрахунком і аналізом перехідного процесу в нелінійному колі.Тут перехідні процеси описують нелінійні диференціальні рівняння, теорія розвязання яких складна і розроблена значно гірше, ніж лінійних. Зараз не існує загального методу (підходу) до рішення нелінійних рівнянь. Існуючі методи не володіють достатньою спільністю і найчастіше можуть бути застосовані до рішення рівнянь лише певного типу. Багато нелінійних рівнянь зараз взагалі не мають аналітичних рішень, або вимагають застосування спеціальних функцій, непридатних в інженерній практиці. Особливо ускладнюється справа в тому випадку, якщо нелінійність кола задана графічно і відсутній достатньо простий математичний опис цієї нелінійності.
У інженерній практиці часто достатньо одержати хоча б орієнтовні розрахункові співвідношення, що дають наближену кількісну оцінку процесів в нелінійному колі. Тому в теорії нелінійних кіл широко розвинені методи наближених рішень.
Існуючі методи аналізу перехідних процесів в нелінійних колах можна класифікувати таким чином:
-по виду операцій, які необхідно виконати для розвязання (вирішення, інтегрування) нелінійних диференціальних рівнянь: а) аналітичні; б) графічні; в) графо-аналітичні; г) чисельні;
-по характеру величини, для якої виконується розрахунок: а) розрахунок для миттєвих значень струмів і напруг; б) розрахунок для миттєвих значень огинаючих струмів і напруг; в) розрахунок для складових, що змінюються поволі.
Аналітичними методами розрахунку вважаються такі, основною операцією яких при визначенні залежностей шуканих струмів і напруг як функцій часу є точне або наближене аналітичне інтегрування диференціальних рівнянь, в якому застосовуються аналітичні вирази характеристик нелінійних елементів кола. Слід мати на увазі, що тільки порівняно прості рівняння (невисокого порядку) зараз мають аналітичне рішення. Гідність аналітичних методів полягає в тому, що вони дають можливість одержати рішення в загальному вигляді, а не для якогось конкретного поєднання параметрів елементів кола. Аналіз такого рішення дозволяє з'ясувати всі особливості перехідного процесу в схемі при зміні параметрів її елементів.
При застосуванні графічних (або графо-аналітичних) методів аналізу перехідних процесів в нелінійних колах основними операціями при визначенні залежностей шуканих струмів і напруг, як функцій часу, є графічні побудови, що супроводжуються деякими чисельними розрахунками. Переваги графічних методів перед аналітичними: а) не потрібна аналітична апроксимація характеристик нелінійних елементів кола, що звільняє рішення від похибки апроксимації; б) дозволяють значно простіше враховувати наявність гістерезису або інших складних характеристик нелінійних елементів. Але слід мати на увазі, що графічні методи (і графо-аналітичні також) застосовні до рішення нелінійних диференціальних рівнянь невисокого порядку (не вище другого).
Зараз розроблено багато способів чисельного рішення нелінійних диференціальних рівнянь. При їх застосуванні рішення обчислюється крок за кроком, а результат розвязання рівняння найчастіше надається у вигляді таблиці відповідних значень змінних кола в часі. Іноді в процесі чисельного рішення застосовують проміжні графічні побудови, що не міняє істоту методу. Будь-яке рівняння може бути розвязане чисельними методами. Для цього повинні бути чисельно задані конкретні значення характеристик всіх елементів і початкові умови. Отримане рішення відповідає саме такому конкретному поєднанню параметрів. Спільність чисельних методів велика, оскільки ними можна скористатися для розвязання будь-якого диференціального рівняння. Проте чисельне рішення складного рівняння вимагає виконання великого об'єму обчислювальних робіт, що зумовлює обовязкове застосування ЕОМ.
Розрахунок для огинаючих струмів і напруг дає можливість, не вдаючись в дрібні деталі процесу усередині кожного періоду діючої в схемі періодичної е.р.с.(або усередині кожного періоду автоколивань в автоколивальній схемі), судити про макроструктуру процесу. Він застосовується не тільки для нелінійних, але і лінійних кіл. Звичайно, точність розрахунку для огинаючих поступається точністю розрахунку за миттєвими значеннями. Проте відносна швидкість розрахунку для огинаючих і можливість судити про макроструктуру перехідного процесу часто виявляються вирішальними чинниками розрахунку для огинаючих. Іноді, де це необхідно, розрахунок для огинаючих доповнюють розрахунками за миттєвими значеннями.
У практичних задачах при виконанні розрахунків найчастіше застосовують поєднання декількох методів. Слід мати на увазі, що досить часто нелінійні характеристики бувають визначені приблизно і можуть істотно змінюватися в часі або при дії будь-яких чинників. Тому швидкість розрахунку, простота і наочність рішення часто бувають більш переважні, ніж точність і повнота математичного опису.
9.2 Аналітичні методи
Як вже наголошувалося, розвязання диференціального рівняння в аналітичному вигляді при аналізі перехідного процесу в нелінійному колі, якщо воно тільки можливе, дає великі переваги – рішення може бути досліджене у всій області його існування. Деякі з методів, що розроблені для розвязання лінійних диференціальних рівнянь, можуть бути поширені і на розвязання нелінійних рівнянь. Дуже часто рішення лінійного диференціального рівняння приймається у вигляді ряду, складеного за ступенями незалежної змінної. Наприклад, передбачається, що рішенням рівняння
є ряд
.
В процесі розвязання ряд підставляють в початкове рівняння і визначають коефіцієнти а0,а1, а2,… .
Метод визначення рішення у вигляді ряду, складеного за ступенями незалежної змінної, в деяких випадках може бути успішно поширений і на нелінійні рівняння. Звичайно, при цьому не вдається встановити відповідність цього ряду будь-якій добре відомій і табульованій функції. Ряд забезпечує лише формальне розвязання рівняння в тому сенсі, що він задовольняє рівнянню, якщо буде в нього підставленим.
Більшість аналітичних методів розв’язання нелінійних рівнянь у такий спосіб хоча і не співпадають в подробицях, але в основному відповідають етапам, представленим на наступній схемі:
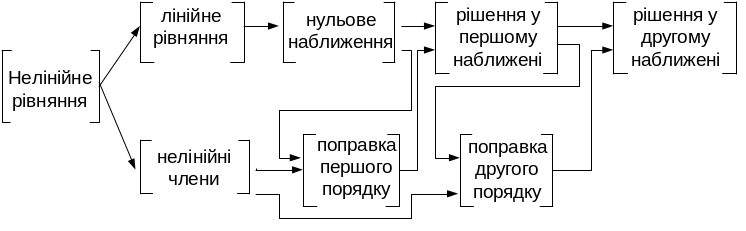
Рисунок 9.1 – Узагальнена схема розв’язання
нелінійних рівнянь аналітичними методами
Суть схеми, зображеної на рис. 9.1, полягає в наступному:
а) початкове нелінійне рівняння ділять на дві частини; одну з них складає лінійне рівняння, достатньо просте, щоб одержати його точне рішення; інша містить всі складові, які приводять до утруднень, і звичайно включають нелінійні члени; в результаті рішення лінійного рівняння одержують деяку функцію, звану нульовим наближенням (або рішенням, що породжує);
б) нульове наближення яким-небудь чином використовують з нелінійними членами початкового рівняння для того, щоб визначити поправку першого порядку;
в) визначену поправку першого порядку об'єднують з нульовим наближенням для отримання рішення початкового рівняння в першому наближені; спосіб об'єднання поправки і нульового наближення визначають особливості методу, що вживається; якщо вплив нелінійності малий, вже одноразове застосування описаної процедури дозволяє отримати рішення у першому наближені, яке має достатньо високу точність;
4) якщо нелінійність значна і рішення у першому наближені не задовольняє вимогам, то можна досягти більшої точності шляхом повторного застосування тієї ж процедури; це приводить до рішення у другому наближені. Подальші повторні застосування теоретично можливі, але на практиці не застосовуються через істотне зростання труднощів обчислень та їх малу ефективність.