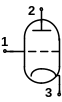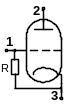33

6 Узагальнені матричні методи

6.1 Відмінність узагальнених матричних методів від звичайних методів

вузлових напруг та контурних струмів

Основна відмінність узагальнених матричних методів від звичайних полягає в наступному. При аналізі схеми методами вузлових напруг або контурних струмів необхідно, в першу чергу, перейти від реальної схеми до еквівалентної, тобто замінити активні компоненти їх лінійними (малосигнальними) моделями (схемами заміщення), що складаються з пасивних двополюсників і керованих джерел струму або напруги. Після цього складаються рівняння для визначення струмів і напруг схеми (або співвідношення між струмами і напругою в окремих гілках), що виникають в результаті дії джерела інформаційного сигналу.

При використанні узагальнених матричних методів вузлових напруг або контурних струмів схема в цілому заміщується матрицею еквівалентних електричних провідностей або опорів, що відображає як конфігурацію, так і властивості деякої лінійної схеми, що апроксимує реальну схему, без переходу до еквівалентної схеми заміщення. Повна матриця (провідністі або опору) схеми складається безпосередньо за лінійною апроксимуючою схемою шляхом підсумовування матриць окремих компонентів схеми. На практиці ця операція виконується вписуванням у відповідні клітки еквівалентної матриці (прямокутної таблиці) значень параметрів матриць компонентів схеми.

Зазвичай, номенклатура компонентів, що входять до складу схеми, невелика. Тому, розглядаючи, кожен з них як багатополюсник, можна заздалегідь скласти матриці (провідністі або опору) цих компонентів і звести їх в таблицю для подальшого використання. Два способи представлення параметрів багатополюсника у вигляді матриці провідності або опору відповідає двом методам аналізу схем – методу вузлових напруг і методу контурних струмів.

6.2 Неавтономний багатополюсник

В узагальнених матричних методах важливу роль відіграє поняття неавтономного багатополюсника. Дамо йому визначення. Неавтономним багатополюсником є компонент або будь-яке складне з'єднання компонентів, що може з'єднуватися з іншими схемами тільки своїми полюсами (затисками). Цей багатополюсник не містить у своєму складі незалежні джерела напруги або струму і тому, коли він від'єднаний від інших схем, на його полюсах немає ні напруг, ні струмів. Якщо розглядати неавтономний багатополюсник як частину складної схеми, то взаємодія його зі схемою враховується або задаючими струмами, що протікають через полюси, або задаючими напругами, прикладеними до його полюсів. Звідси витікає два способи запису рівнянь неавтономного багатополюсника.

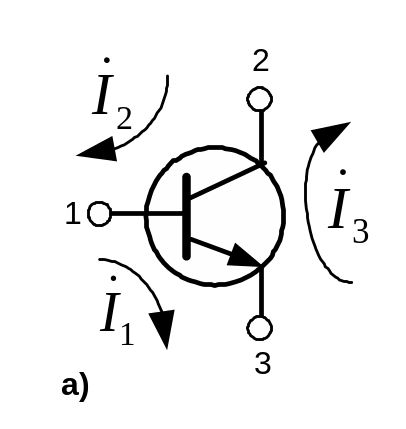
Розглянемо багатополюсник, що має m полюсів (рис. 6.1). Нехай в його полюси втікають струми , які враховують взаємодію багатополюсника з останньою частиною схеми.

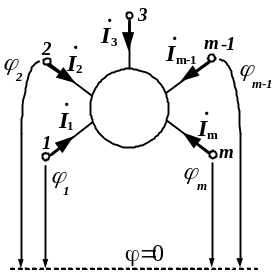
Рисунок 6.1 – Схема до аналізу багатополюсника

за методом вузлових напруг

Узагальнюючи метод вузлових напруг на електронні схеми, що містять багатополюсні компоненти, запишемо для багатополюсника систему рівнянь на основі вказаного методу. У якості незалежних величин при запису рівнянь приймаємо потенціали полюсів , що відлічуються щодо деякого базисного вузла (φ=0), обраного зовні багатополюсника (такий вибір базисного вузла становить всі вузли схеми у однакове положення). Отже, для багатополюсника, схема якого наведена на рис. 6.1, запишемо наступну систему, що містить m рівнянь:

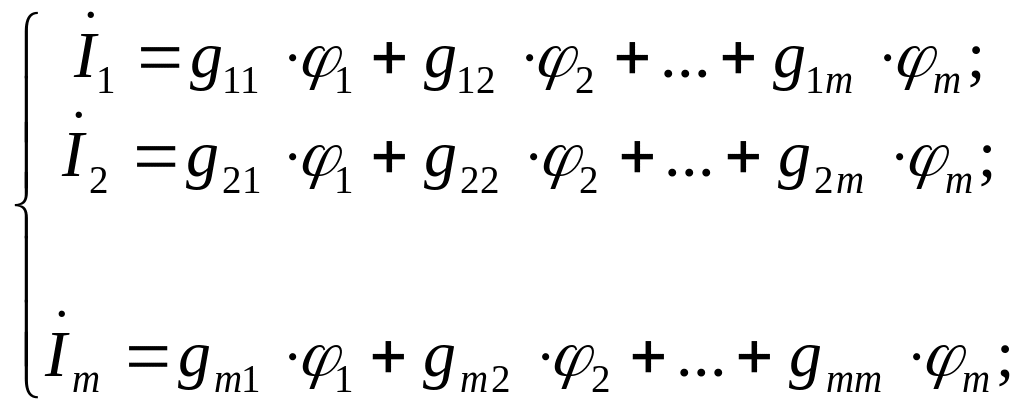(6.1)

тут: g_ii – сумарна провідність всіх гілок багатополюсника, що сходяться в його i-му полюсі; g_ij - сумарна провідність всіх гілок багатополюсника, що з’єднують i-й полюс з j-м.

Система (6.1) може бути записана у матричній формі наступним чином:

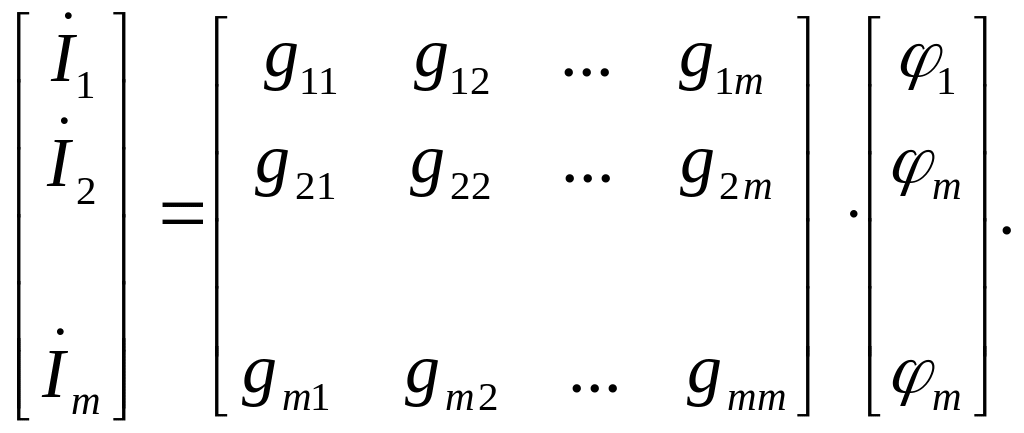(6.2)

Квадратна матриця m-го порядку, що складена з коефіцієнтів рівнянь системи (6.1) і записана в правій частині (6.2), можна розглядатися як узагальнений параметр багатополюсника, що повністю характеризує його. Всі елементи цієї матриці мають розмірність електричної провідності, тому її називають повною матрицею провідності багатополюсника і позначають як [G].

Зазначимо, що в системі (6.1) не визначено незалежне рівняння і всі рівняння системи являються залежними; тобто будь-яке з цих рівнянь можна отримати з (m-1) останніх. Тому не всі елементи повної матриці провідності [G] є незалежними, а сама матриця є особливою. Відповідно до цього: а) сума елементів кожного рядка матриці дорівнює 0, б) сума елементів кожного стовпця матриці дорівнює 0. Дані властивості матриці [G] є корисними і застосовуються при складанні повних матриць параметрів активних багатополюсників.

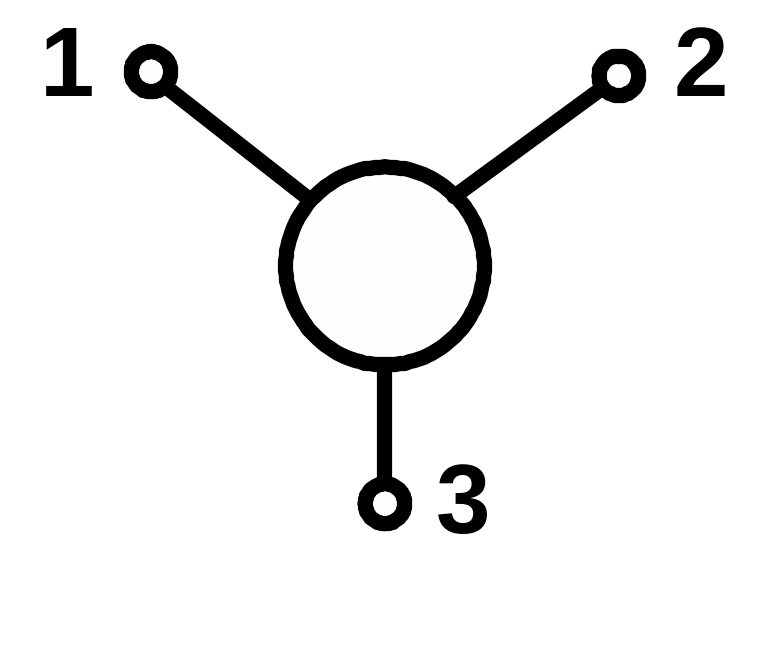
Узагальнюючи метод контурних струмів на електронні схеми, що містять багатополюсні компоненти, можна записати для неавтономного багатополюсника систему рівнянь, де у якості незалежних величин застосовуються контурні струми , а у якості залежних - напруги між полюсами багатополюсника (схема на рис. 6.2).

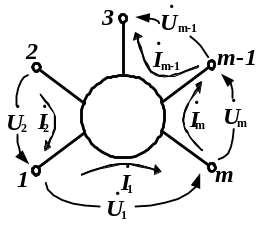
Рисунок 6.2 - Схема до аналізу багатополюсника

за методом контурних струмів

У загальному вигляді система рівнянь за методом контурних струмів для наведеної на рис. 6.2 схеми може бути записана наступним чином:

(6.3)

Або в матричній формі:

(6.4)

Квадратна матриця m-го порядку, що складена з коефіцієнтів рівнянь системи (6.3) і записана в правій частині (6.4), повністю характеризує багатополюсник і є узагальненим параметром багатополюсника. Всі елементи цієї матриці мають розмірність електричного опору, тому її називають повною матрицею опору багатополюсника і позначають як [Z]. Повна матриця опору [Z] в (6.4), как і матриця провідності [G] в (6.2), є особливою і має такі ж властивості.

Зазначимо наступне: якщо для багатополюсника вже відома (складена) якась з повних матриць (наприклад, матриця провідності [G]), то іншу повну матрицю (матрицю опору [Z]) можна отримати з відомої шляхом простих перерахунків (як і матрицю [Z] з матриці [G]). Не зупиняючись на доказі формул переходу, надамо залежності між повними матрицями електричної провідності і опору для триполюсника з урахуванням прийнятих на рис. 6.1 і 6.2 схемах позначення полюсів і контурів багатополюсників (полюс 1 - що керує).

		1	2	3
		g22	g32	g12	1
		g23	g33	g13	2 (6.5)
		g21	g31	g11	3
		1	2	3
		Z33	Z13	Z23	1
		Z31	Z11	Z21	2 (6.6)
		Z32	Z12	Z22	3

Рисунок 6.3 – Залежності між елементами повних матриць електричного

опору і електричної провідності неавтономного триполюсника

6.3 Матричні параметри активних багатополюсників електронних схем

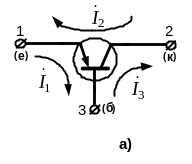
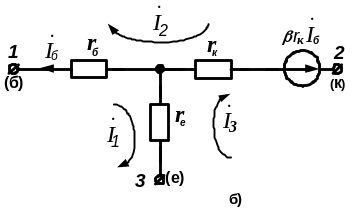
6.3.1. Транзистор біполярний. Побудуємо повну матрицю опору біполярного транзистору (БПТ), як неавтономного багатополюсника, формально дотримуючись методики, що була застосована у розділі 4 для схем із керованими джерелами. Приймаємо, що транзистор працює в схемі у включені зі спільною базою (рис. 6.4а). Для побудови матриці використаємо схему заміщення БПТ у вигляді Т – подібної фізичної моделі. Вважаємо, що в гілках транзистора, як багатополюсника, протікають контурні струми , як це показано на рис. 6.4 (нумерація контурних струмів і полюсів тут відповідає рис. 6.3).

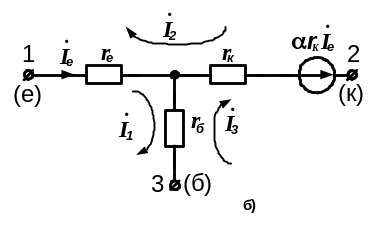
Рисунок 6.4 – До складання повної матриці опору БПТ

у включені із спільною базою

а) Формально застосовуючи методику, викладену в розділі 4, записуємо для схеми на рис. 6.4б матрицю опору пасивної частини схеми - матрицю [Z]′:

	1	2	3
	rе + rб	-rе	-rб	1
[Z]′=	-rе	rе + rк	-rк	2
	-rб	-rк	rб + rк	3 .

б) Складаємо таблицю керованих джерел, вписуючи до неї параметри джерел, що керують, і струми джерел, що керують, виражені через контурні струми схеми на рис. 6.4б. В цій схемі є лише одне кероване (залежне) джерело, е.р.с. якого дорівнює .

е.р.с. джерела	параметр, що керує	струм, що керує
	αrк		.

в) Відповідно до прийнятої методики записуємо також матрицю взаємозв’язку – матрицю [Z]′′ (в матрицю вписуємо параметр αr_к керованого джерела):

	1	2	3
	0	0	0	1
[Z]′′=	αrк	-αrк	0	2
	-αrк	αrк	0	3 .

г) Записуємо шукану повну матрицю опору БПТ шляхом додавання матриці взаємозв’язку до матриці пасивної частини схеми ([Z]= [Z]′+ [Z]′′):

	1	2	3
	rе + rб	-rе	-rб	1
[Z]=	αrк –rе	-αrк+rе+rк	-rк	2
	- αrк - rб	αrк - rк	rб + rк	3 .

д) Із використанням повної матриці електричної провідності БПТ в параметрах фізичної моделі, що наведена вище, отримана повна матриця провідності [G] біполярного транзистора шляхом застосування формули (6.6):

	1	2	3
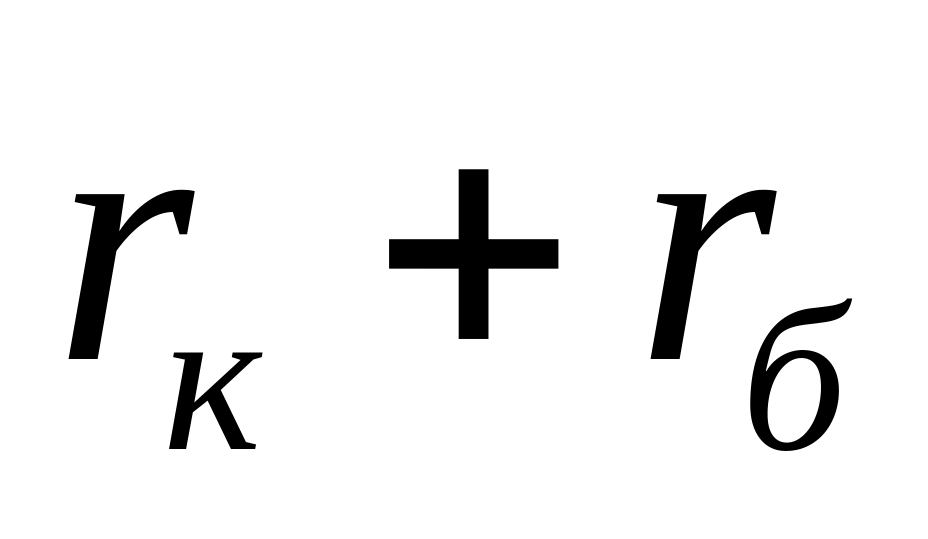
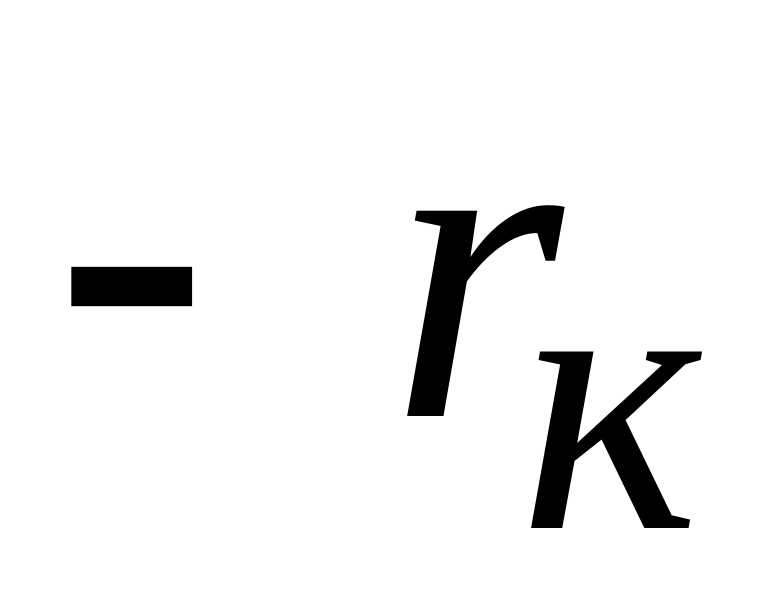
				1
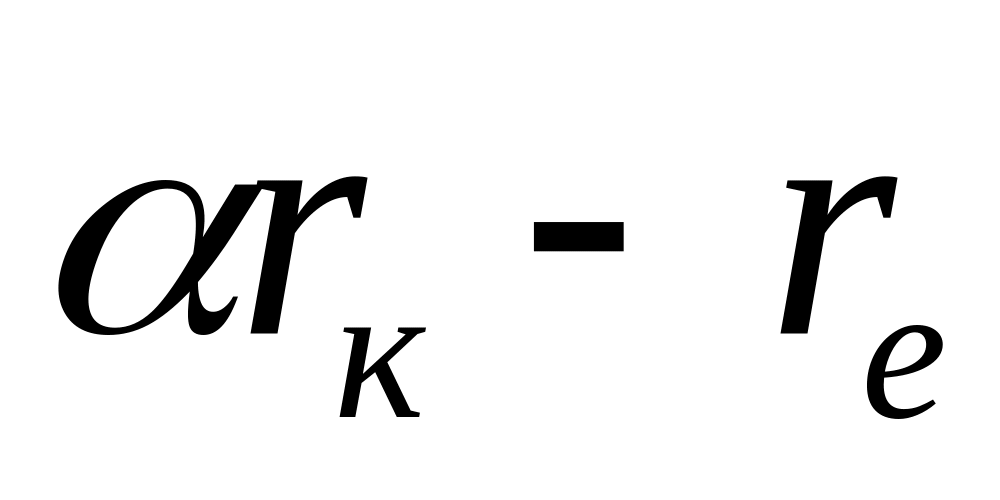
				2
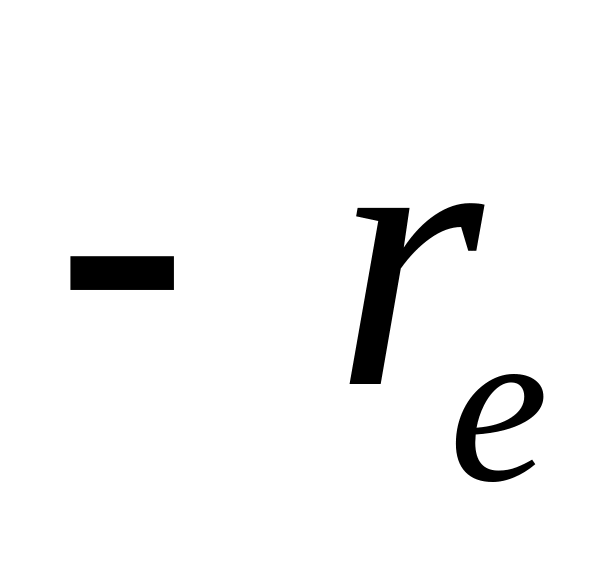
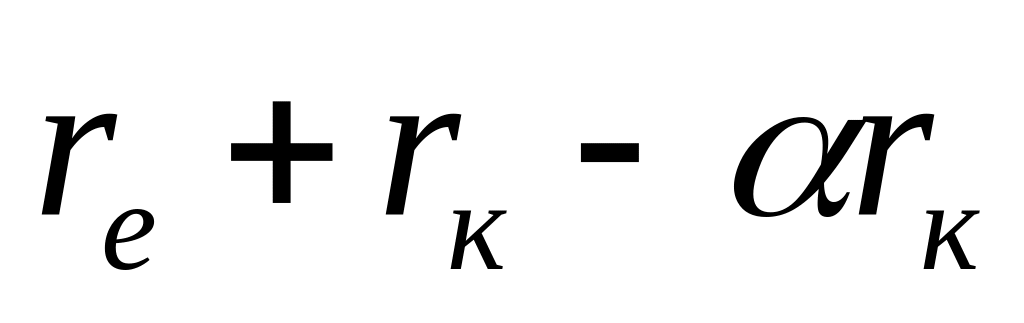
				3 ,

де

е) Відомо, що між параметрами фізичної моделі БПТ і R-параметрами транзистора, як чотириполюсника, існує наступний зв'язок:

R_11б=r_е+r_б; R_12б=r_б; R_21б =r_б+ r_к; R_22б = r_к+r_б.

Тому матрицю опору [Z] БПТ можна записати у наступному вигляді:

	1	2	3
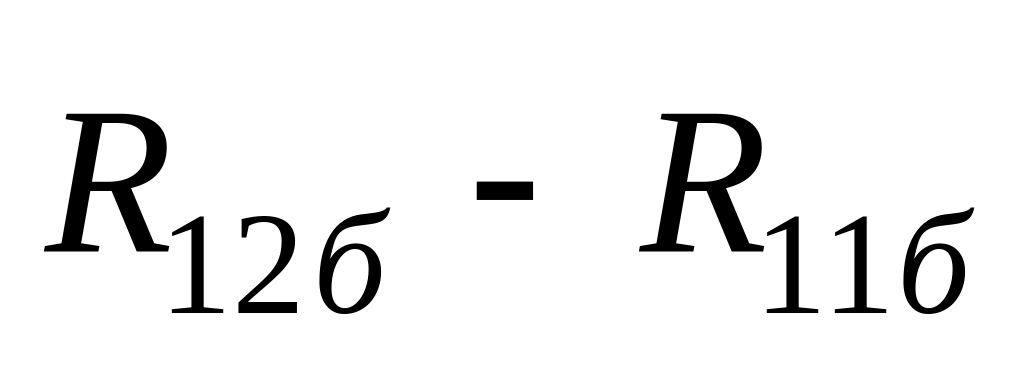
				1
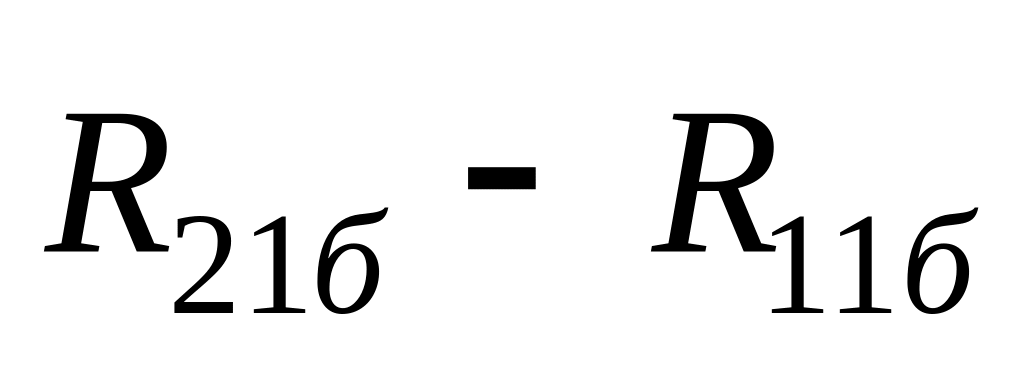
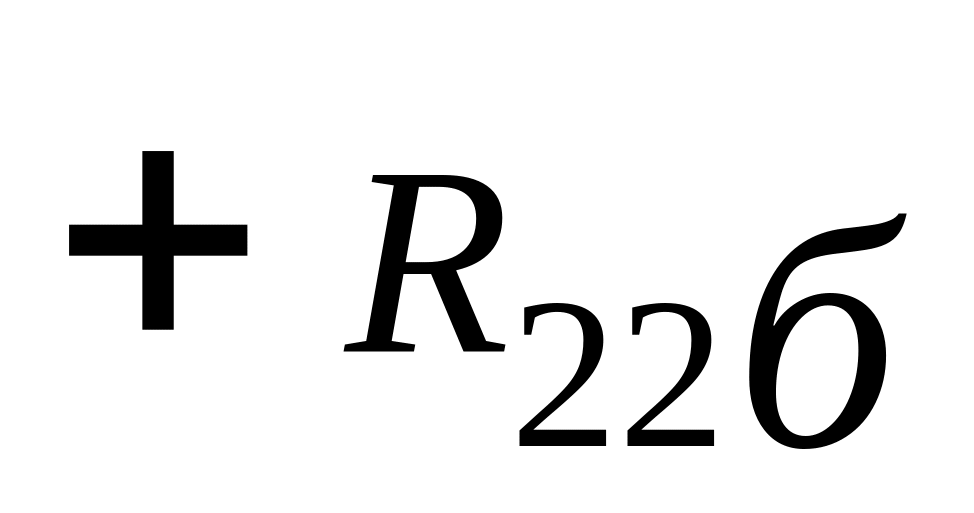
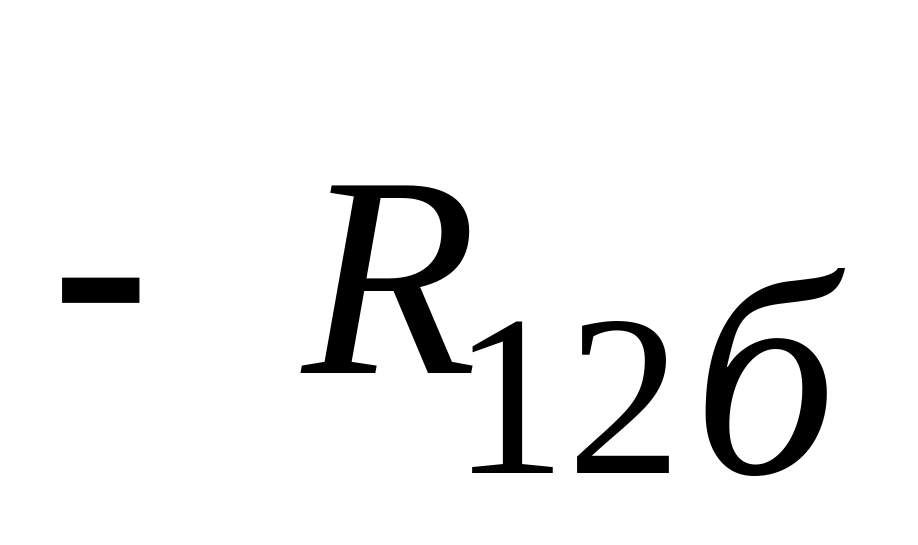
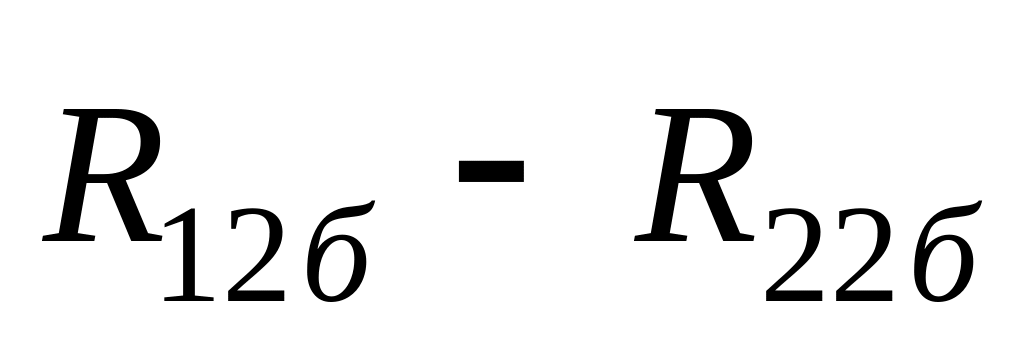
[Z]=				2
				3 .

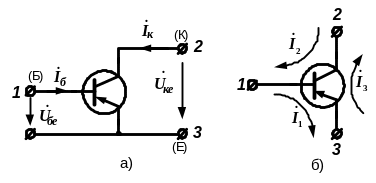
ж) Повні матриці опору і провідності БПТ, що отримані вище, зазвичай використовуються на низьких частотах, де параметри транзисторів вважаються дійсними числами. На високих частотах параметри транзистора залежать від частоти і є комплексними числами. Зазвичай, як початкові рівняння, при визначенні параметрів БПТ на високих частотах застосовують рівняння в системі у- параметрів транзисторів у включенні із спільним емітером (рис. 6.5а):

Рисунок 6.5 - До складання повної матриці провідності БПТ

на високих частотах

Із застосуванням наведеної системи рівнянь і схеми на рис. 6.5б побудована повна матриця провідності біполярного транзистора, як неавтономного триполюсника, що може застосовуватись на високих частотах:

	1	2	3
				1
				2
				3 .

Параметри транзистора , що надходять до наведеної повної матриці, можна взяти із довідкової літератури відповідно до типу БПТ, застосованого в досліджуваній схемі.

6.3.2. Транзистор польовий. Повну матрицю провідності польового транзистора (ПТ) отримаємо по методиці побудови матриці провідності схеми із керованими джерелами, що була розглянута у розділі 4. Для складання матриці скористаємося малосигнальною моделлю ПТ з керованим джерелом струму (рис. 6.6). Приймаємо, що транзистор включений в схему із спільним витоком і працює в режимі нульового струму затвору. Нумерація виводів транзистора, як багатополюсника, наведена на рис. 6.6 і відповідає прийнятій на рис. 6.3 схемі позначення полюсів триполюсника; потенціали затвору φ₁, стоку φ₂ і витоку φ₃ відлічуються щодо деякого базисного вузла (φ=0), обраного зовні транзистора.

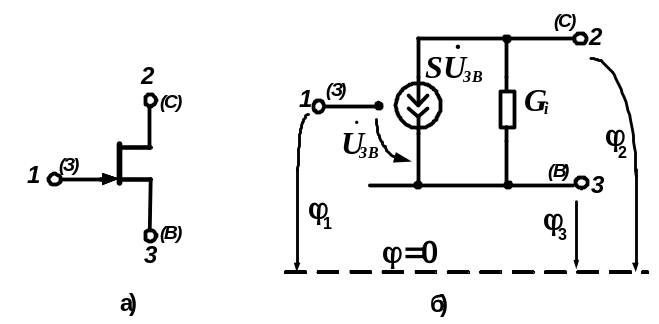
Рисунок 6.6 - До складання повної матриці провідності ПТ

а) Формально застосовуючи методику, викладену в розділі 4, записуємо відповідно до рис. 6.6б матрицю провідності пасивної частини схеми - матрицю [g]′:

	1	2	3
	0	0	0	1
[g]′=	0	Gi	-Gi	2
	0	-Gi	Gi	3 .

б) Складаємо таблицю керованих джерел, записуючи до неї параметри джерел, що керують, і напруги джерел, що керують, які виражені через потенціали полюсів ПТ відповідно до рис. 6.6б. В схемі є лише одне кероване джерело, струм якого дорівнює .

струм джерела	параметр, що керує	напруга, що керує
			.

2. Записуємо матрицю взаємозв'язку – матрицю [g]′′ (в матрицю вписуємо параметр керованого джерела ):

	1	2	3
	0	0	0	1
[g]′′=	+S	0	-S	2
	-S	0	+S	3 .

в) Записуємо повну матрицю провідності ПТ шляхом додавання матриці взаємозв’язку до матриці пасивної частини схеми ([G]= [g]′+ [g]′′):

	1	2	3
	0	0	0	1
[G]=	+S	Gi	-Gi -S	2
	-S	-Gi	Gi +S	3 .

6.3.3. Електронні лампи. Електронна лампа при аналізі схеми може розглядатися як багатополюсник, кількість полюсів якого дорівнює кількості всіх її електродів - сіток, аноду, катоду. При складанні повної матриці лампи нумерацію її електродів, як полюсів неавтономного багатополюсника, слід виконувати порядковими номерами від 1 до m відповідно до наведеного нижче рис. 6.7.

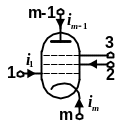
Рисунок 6.7 –Схема нумерації електродів лампи,

як полюсів неавтономного багатополюсника

Перша сітка лампи (сітка, що керує) завжди є першим полюсом багатополюсника; наступні сітки (екранна, антидинатронна і т. д.) нумеруються як 2-й, 3-й і т. д. до (m-2)-й полюс; анод завжди (m-1) -й полюс, катод – m-й.

Кожен із струмів, що втікає в лампу через її електроди, є функцією напруг, прикладених до всіх її електродів, тобто:

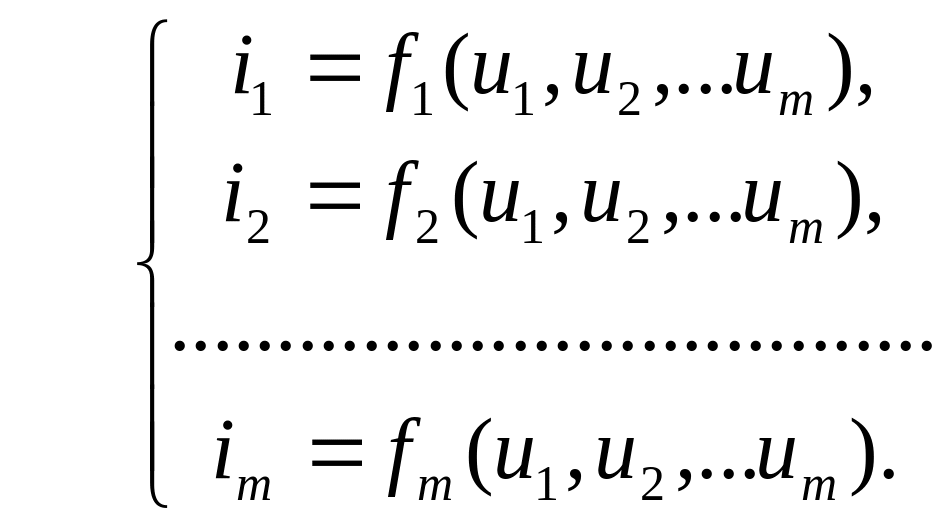(6.7)

Наведені вище залежності (6.7) в загальному випадку є нелінійними функціями, проте при невеликих змінах потенціалів електродів щодо їх значень в точці спокою залежності можна вважати лінійними. Тому, якщо виконати розкладання вказаних залежностей в точці спокою в ряд Тейлора і обмежитись тільки лінійними членами розкладання, отримаємо:

(6.8)

Оскільки при малосигнальному аналізі електронних систем зазвичай мають інтерес не абсолютні значення струмів і напруг, а саме їх прирости, систему (6.8) можна записати в символічній формі:

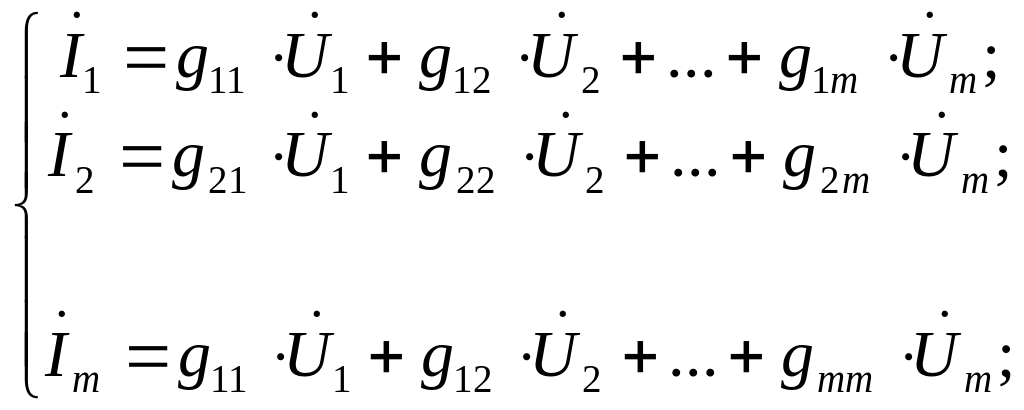(6.9а)

або так: . (6.9б)

Величина є внутрішня провідність лампи по k-му електроду; вона характеризують приріст струму k-го електроду при зміні напруги цього електроду і незмінних значеннях напруг інших електродів. Величина характеризує зміну струму k-го електроду при зміні напруги S-го електроду і незмінних значеннях напруг інших електродів, є крутизною струму залежно від напруги . Внутрішні провідності і крутизни є параметрами лампи, які можуть бути визначені або шляхом безпосередніх вимірювань, або шляхом обчислень по відповідних характеристиках. Отже, повна матриця провідності електронної лампи, що складається з коефіцієнтів правих частин рівнянь системи (6.9), тобто з внутрішніх провідностей і крутизн , уявляє собою особливу матрицю і є узагальненим параметром лампи, що цілком її характеризує; в загальному випадку вона може бути записана так:

[G] =	1	2	…	m
	g11	g12	…	g1m	1
	g21	g22	…	g2m	2
	…	…	…	…	…
	gm1	gm2	…	gmm	m

Зазвичай внутрішня провідність позначається як G_i, а крутизна – як S. Тому повна матриця провідності лампи у загальному випадку може бути записана так:

[G]= 1 2 3 … m Gi1 S12 S13 … S1m 1 S21 Gi2 S23 … S2m 2 … … … … … Sm1 Sm2 … Gim m

. (6.10)

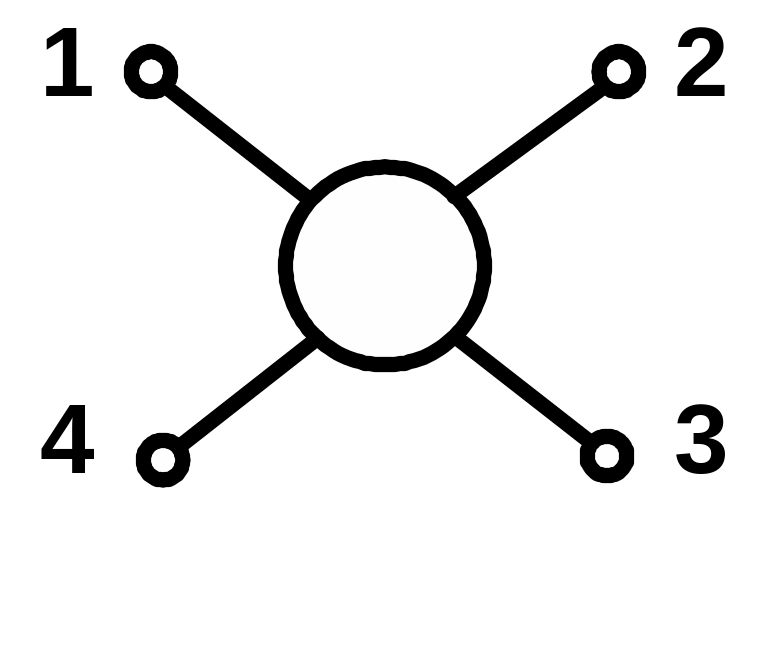
Пентод, у якого третя сітка сполучена з катодом (див. рис. 6.8), може вважатися в схемі неавтономним чотириполюсником. Його повна матриця провідності є особливою матрицею, що має чотири рядки і чотири стовпчики, і з урахуванням виразу (6.10) записана нижче (номера рядків і стовпчиків наведеної матриці відповідають номерам полюсів пентода, як неавтономного чотириполюсника, згідно рис. 6.8):

Рисунок 6.8 - Нумерація електродів пентода, як полюсів неавтономного чотириполюсника	[G]=	1	2	3	4
						1
						2
						3
						4.

Тріод, що має лише одну сітку, уявляє собою триполюсник. У загальному випадку повна матриця провідності тріода може бути записана так:

			1	2	3
						1
						2
						3 .

Ідеальний тріод, що працює без сіткових струмів (при негативному зміщені на сітці), характеризується матрицею, у яку входять тільки внутрішня провідність G_i і крутизна характеристики S:

	1	2	3
	0	0	0	1
				2
				3 .

Зазначимо, що для ідеального тріода матриця опору не існує, оскільки деякі її елементи звертаються в нескінченність. Дійсно, якщо застосувати формулу (6.5) для переходу від матриці [G] до матриці [Z], то коефіцієнт формули звертається у нескінченність внаслідок того, що для ідеального тріода знаменник наведеного коефіцієнта дорівнює 0 (g₁₁= 0 і g₁₂ = 0)

Часто використовується схема, в якій між сіткою і катодом тріода включається опір R . Повна матриця провідності ідеального тріода, що працює без сіткових струмів, в такому включенні має наступний вигляд:

	[G]=	1	2	3
			0		1
					2
					3

В наведеній вище схемі включення тріоду струм, що втікає в перший полюс (сітку), дорівнює , відповідно . Для такої схеми включеня тріоду матриця [Z] існує і може бути отримана застосуванням формули (6.5), бо коефіцієнт цієї формули не звертається у нескінченність і не перетворює в нескінченність елементи матриці [Z].

6.4 Узагальнений метод вузлових напруг

Аналіз схеми методом вузлових напруг потребує застосування матрично - векторних параметрів схеми – задаючого вектору і матриці провідності схеми. Запис задаючого вектора схеми, що містить багатополюсні елементи, нічим не відрізняється від запису задаючого вектора схеми, що складається тільки з двополюсних елементів: компоненти задаючого вектора дорівнюють алгебраічним сумам струмів, що втікають у вузли схеми. Повна матриця провідності досліджуваної схеми при використанні узагальненого методу вузлових напруг визначається шляхом сумування повних матриць провідності неавтономних багатополюсників (або підсхем), що входять до складу схеми, відповідно до формули:

,

де - повна матриця провідності i-го неавтономного багатополюсника; - повна матриця провідності досліджуваної схеми.

При складанні повної матриці провідності (також і опору) досліджуваної схеми використовують робочу (розрахункову) схему, що дійсна лише для змінних складових струмів і напруг в досліджуваній схемі (її побудова розглянута у розділі 4). Повна матриця провідності схеми складається у такий спосіб:

1) Нумерують всі вузли робочої схеми порядковими номерами від 1 до n (у якості базисного вузла, потенціал якого вважається φ₀=0, обирається вузол зовні схеми).

2) Готують квадратну таблицю з кількістю рядків і стовпців, що дорівнює кількості пронумерованих вузлів схеми: (n X n). Так, для схеми, наведеної на рис. 6.9, що має 5 вузлів, необхідно підготувати таблицю, що має 5 рядків і 5 стовпчиків.

3) В схемі виділяють неавтономні багатополюсники. Так, у наданій на рис. 6.9 схемі є три двополюсники g₁, g₂, g_н, один триполюсник (I) і один чотириполюсник (II).

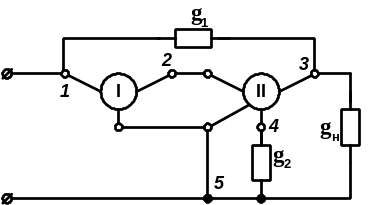
Рисунок 6.9 – До складання повної матриці провідності схеми

за узагальненим методом вузлових напруг

4) Записують повну матрицю провідності для кожного неавтономного багатополюсника схеми, вважаючи його у - параметри відомими. Слід зазначити, що повні матриці провідності неавтономних багатополюсників, які зустрічаються в аналізі (розрахунку) електронних схем (кількість їх не дуже значна), складають заздалегідь і розміщують для подальшого використання у відповідних таблицях.

У загальному випадку повна матриця провідності двополюсника має розмір 2×2 і записується наступним чином:

		1	2
	[Gдв]=	g	–g	1 (6.10а)
		–g	g	2 .

Повні матриці провідності триполюсника і чотириполюсника в загальному випадку мають вигляд:

		1 (1)	2 (2)	3 (5)
	[Gтр]=	g11	g12	g13	1 (1)
		g21	g22	g23	2 (2) (6.10б)
		g31	g32	g33	3 (5) .

		1 (2)	2 (3)	3 (4)	4 (5)
	[Gчт]=	g'11	g'12	g'13	g'14	1 (2)
		g'21	g'22	g'23	g'24	2 (3) (6.10в)
		g'31	g'32	g'33	g'34	3 (4)
		g'41	g'42	g'43	g'44	4 (5) .

Розмір кожної наведеної вище повної матриці дорівнює кількості полюсів відповідного неавтономного багатополюсника, а номера рядків і стовпців матриць без дужок відповідають номерам полюсів багатополюсників на їх схемах (6.10а, б, в).

5) У повній матриці провідності кожного багатополюсника в нумерації рядків і стовпців замінюють номери полюсів багатополюсника (цифри без дужок) відповідними номерами вузлів робочої схеми, з якими сполучені полюси багатополюсника – цифри в дужках в нумерації рядків і стовпців матриць. Тепер матриця містить інформацію не тільки про параметри багатополюсника, але й про положення, яке він займає в досліджуваній схемі. Нова нумерація (в дужках) рядків і стовпців матриці багатополюсника вказує, в яку клітину повної матриці провідності схеми слід вписувати відповідний елемент повної матриці провідності цього неавтономного багатополюсника.

6) У клітини таблиці, попередньо виготовленої у п. 2, вписують відповідно до п.5 елементи матриць всіх багатополюсників схеми, підсумовуючи їх. Так, повна матриця провідності схеми, наведеної на рис. 6.9, має вигляд:

	1	2	3	4	5
				0		1
						2
[G]=						3
	0					4
						5 .

7) Один із вузлів схеми обирають у якості базисного і формують скорочену матрицю провідності схеми шляхом викреслення рядка і стовпця повної матриці, номери яких дорівнюють номеру базисного вузла (для розрахунку вторинних вихідних параметрів схеми за формулами, отриманими раніше у розділі 3, можна застосовувати тільки скорочену матрицю!). Як базисний доцільно вибирати той вузол, в якому сходиться найбільша кількість гілок схеми. У підсилювальних схемах найчастіше цей вузол є заземлений. Також із матриці слід виключити внутрішню провідність джерела вхідного сигналу схеми і провідність навантаження g_н. Так, для наведеної схеми (рис. 6.9) є сенс обрати, як базисний, 5-й вузол. Тому слід викреслити в повній матриці схеми п'ятий рядок і 5-й стовпчик і виключити з неї провідність навантаження g_н . В підсумку скорочена матриця схеми має наступний вигляд:

	1	2	3	4
[Gск]=				0	1
					2
					3
	0				4 .

Процедуру складання скороченої матриці провідності досліджуваної схеми при аналізі за узагальненим методом вузлових напруг можна спростити. Для цього одразу приймають один з вузлів робочої схеми як базисний і записують скорочену матрицю схеми з урахуванням тільки всіх пасивних двополюсників (дивись розділ 3). Потім в цю матрицю (таблицю) вносять елементи матриць багатополюсників. Якщо якийсь з полюсів багатополюсника виявляється сполученим з базисним вузлом схеми, то відповідно номеру цього полюса рядок і стовпець в повній матриці багатополюсника викреслюють і не вписують в скорочену матрицю провідності схеми.

Приклад 6.1. Скласти скорочену матрицю провідності схеми підсилювача на біполярних транзисторах (на рис. 6.10 наведена робоча схема підсилювача).

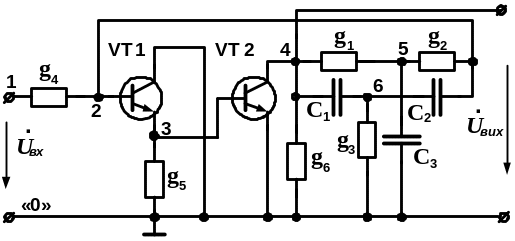
Рисунок 6.10 – Робоча схема підсилювача на біполярних транзисторах

1) Виконуємо нумерацію вузлів робочої схеми: обираємо у якості базисного (вузол «0») заземлений вузол; позначаємо останні вузли схеми цифрами 1, 2, 3 ... 6; записуємо скорочену матрицю провідності схеми (розміром 6×6) з урахуванням тільки двохполюсних елементів (без транзисторів):

	1	2	3	4	5	6
			0	0	0	0	1
			0	0			2
	0	0		0	0	0	3
	0	0	0				4
	0		0			0	5
	0		0		0		6 .

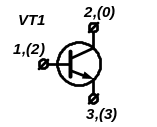
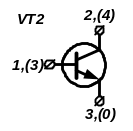
2) Записуємо повні матриці провідності транзисторів VT1 і VT2 (обидва працюють у включенні зі спільним емітером) вважаючи, що їх у-параметри відомі (дивись розділ 6.3.1).

		1 (2)	2 (0)	3 (3)
					1 (2)
					2 (0)
					3 (3) .

		1 (3)	2 (4)	3 (0)
					1 (3)
					2 (4)
					3 (0) .

У повній матриці провідності кожного транзистора в попередній нумерації рядків і стовпців (цифри без дужок) замінюємо номери полюсів транзистора, як неавтономного багатополюсника, відповідними номерами вузлів робочої схеми підсилювача, з якими сполучені полюси транзистора – цифри, що наведені в дужках в нумерації рядків і стовпців матриць. Тепер кожна матриця містить інформацію не тільки про параметри, але й про положення транзистора, яке він займає в досліджуваній схемі.

3) Складаємо скорочену матрицю провідності досліджуваної схеми шляхом внесення елементів матриць транзисторів у відповідні клітини матриці пасивної частини схеми , що була складена при виконанні п. 1; при цьому враховуємо наступне: а) у транзистора VT1 виведення колектора сполучене з базисним вузлом, тому другий стовпчик і другий рядок матриці з номерами „(0)” викреслюємо, а їх елементи не вписуємо в матрицю схеми; б) у транзистора VT2 таку ж процедуру виконуємо для виведення емітера. В підсумку скорочена матриця провідності досліджуваної схеми підсилювача має наступний вигляд:

	1	2	3	4	5	6
			0	0	0	0	1
				0			2
	0				0	0	3
	0	0					4
	0		0			0	5
	0		0		0		6 .

6.5 Узагальнений метод контурних струмів

Аналіз схеми методом контурних струмів потребує застосування матрично - векторних параметрів досліджуваної схеми –вектору задаючих напруг і матриці опору схеми. Спосіб запису вектора задаючих напруг для електронних схем, що містять багатополюсники, нічим не відрізняються від способу його запису для розглянутих раніше схем електричних кіл з двополюсними елементами: його компоненти дорівнюють алгебраічним сумам задаючих напруг у відповідних контурах схеми. Повна матриця опору електронної схеми визначається шляхом сумування повних матриць неавтономних багатополюсників (підсхем), що входять до складу досліджуваної схеми, і складаєтся так:

1) В робочій схемі досліджуваного кола обирають систему контурних струмів так, щоб вони протікали у всіх гілках схеми, і нумерують струми (контури) цифрами від 1 до n. Потім в схемі виділяють неавтономні багатополюсники і записують для них повні матриці опору. Так, в схемі, що наведена на рис. 6.12, обираємо систему з п’яти контурних струмів (контурів) і нумеруємо їх цифрами від 1 до 5 (слід звернути увагу на 5–й контур, що вміщує вхідну напругу схеми, падіння напруги на гілках триполюсника і чотирихполюсника та резисторі навантаження схеми Z_н). В схемі виділяємо п’ять неавтономних багатополюсників: три двополюсники – Z₁, Z₂ і Z_н; один триполюсник – I; один чотириполюсник – II.

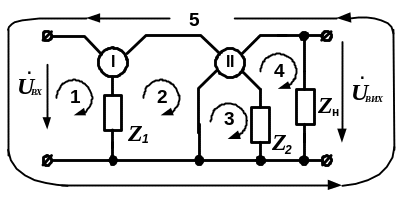
Рисунок 6.12 – До складання повної матриці опору схеми

за узагальненим методом контурних струмів

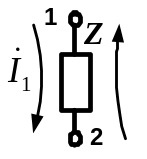
Записуємо для кожного багатополюсника повну матрицю опору, вважаючи, що Z- параметри їх відомі. Матриця опору двополюсника має наступний вигляд:

		1		2
	[Zдв]=	Z	-Z		1
		-Z	Z		2 (6.13а)

Повні матриці опору триполюсника і чотириполюсника в загальному вигляді можуть бути записані наступним чином:

		1 (2)	2 (5)	3 (2)
		Z11	Z12	Z13	1 (1)
	[ZTP]=	Z21	Z22	Z23	2 (5) (6.13б)
		Z31	Z32	Z33	3 (2) .

		1 (2)	2 (5)	3 (4)	4 (3)
	[ZЧТ]=	Z′11	Z′12	Z′13	Z′14	1 (2)
		Z′21	Z′22	Z′23	Z′24	2 (5)
		Z′31	Z′32	Z′33	Z′34	3 (4) (6.13в)
		Z′41	Z′42	Z′43	Z′44	4 (3) .

Розмір кожної наведеної повної матриці дорівнює кількості зовнішніх контурів в схемі 6.13а, 6.13б або 6.13в відповідного неавтономного багатополюсника; номери рядків і стовпців матриць без дужок дорівнюють номерам зовнішніх контурних струмів, що втікають у відповідні полюси багатополюсника на їх схемах 6.13а, 6.13б або 6.13в, тобто номерам зовнішніх контурів багатополюсника.

Слід зазначити, що повні матриці опору неавтономних багатополюсників, які зустрічаються в аналізі (розрахунку) електронних схем (кількість їх не дуже значна), складають заздалегідь і розміщують для подальшого використання у відповідних таблицях.

2) У повній матриці опору кожного неавтономного багатополюсника в нумерації рядків і стовпців замінюють номери зовнішніх контурів багатополюсника (цифри без дужок) відповідними номерами обраних контурних струмів схеми, з якими співпадають ці контури – номери рядків і стовпців матриць в дужках. Тепер матриця містить інформацію не тільки про параметри багатополюсника, але й про положення, яке він займає в схемі. Одночасно нова нумерація рядків і стовпців вказує в яку клітину повної матриці досліджуваної схеми слід вписувати відповідний елемент повної матриці опору цього багатополюсника.

3) У квадратну таблицю розміром n X n вписують елементи матриць багатополюсників, підсумовуючи їх. Так, для схеми, наведеної на рис. 6.12, повна матриця опору має розмір 5 X 5 (5 рядків і 5 стовпців) і виглядає наступним чином:

	1	2	3	4	5
			0	0		1
						2
[Z]=	0					3
	0					4
			0			5 .

5) Один з контурів схеми приймається у якості базисного і формується скорочена матриця опору схеми шляхом викреслювання в повній матриці рядка і стовпця з номером базисноого контура (для розрахунку вторинних вихідних параметрів схеми за формулами, отриманими раніше у розділі 3, можна застосовувати тільки скорочену матрицю!). Базисним контуром доцільно вибирати той, до якого надходить найбільша кількість гілок неавтономних багатополюсників. У підсилювальних схемах найчастіше це контур, до якого надходять вхідна та вихідна напруги схеми. Також із матриці слід виключити внутрішній опір джерела вхідного сигналу схеми і опір навантаження Z_н. Так, в схемі на рис. 6.12 обираємо базисним зовнішній (5-й) контур, викреслюємо в повній матриці 5-й рядок і 5-й стовпець і отримуємо скорочену матрицю опору схеми:

	1	2	3	4
[Zск]=			0	0	1
			0		2
					3
	0				4 .

6) Процедуру складання скороченої матриці опору схеми при аналізі за узагальненим методом контурних струмів можна спростити. Для цього одразу обирають один з контурів схеми як базисний (його позначають номером „0”), а всі останні нумерують цифрами від 1 до n. Спочатку записують скорочену матрицю опору схеми (вона має розмір n X n) з урахуванням тільки пасивних двополюсників. Потім в цю матрицю (таблицю) вносять параметри матриць багатополюсників. Якщо якийсь з зовнішніх контурів багатополюсника виявляється співпадаючим з базисним контуром схеми, то рядок і стовпець повної матриці опору багатополюсника з номером базисного контура викреслюють і не вписують в скорочену матрицю схеми. В отриманій матриці слід виключити внутрішній опір джерела вхідного сигналу схеми і опір навантаження Z_н.

Слід зазначити, що узагальнений метод контурних струмів може бути застосований до аналізу лише планарного (плоского) кола, схему якого можна викреслити на площині без перетину зв'язків. Непланарне коло без перетворень неможна представити у вигляді схеми на площині без перетину зв'язків.

Приклад 6.2. Записати скорочену матрицю опору підсилювача на біполярних транзисторах, робоча схема якого наведена нижче на рис. 6.13.

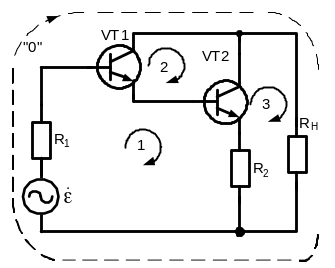
Рисунок 6.13 – Схема підсилювача на біполярних транзисторах,

що підготовлена до складання повної матриці опору

1) В робочій схемі підсилювача обираємо систему контурних струмів так, щоб всі гілки схеми увійшли до них – із схеми видно, що система повинна містити не менше 4-х контурних струмів (вони зображені на попередній схемі); обираемо у якості базисного контур з номером «0»; записуємо скорочену матрицю опору схеми без урахування транзисторів (вона має розмір 3 X 3):

	1	2	3
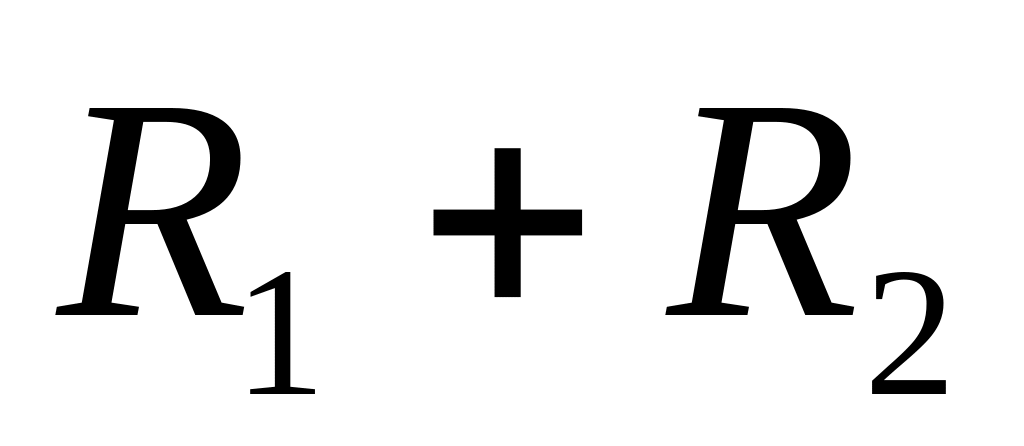
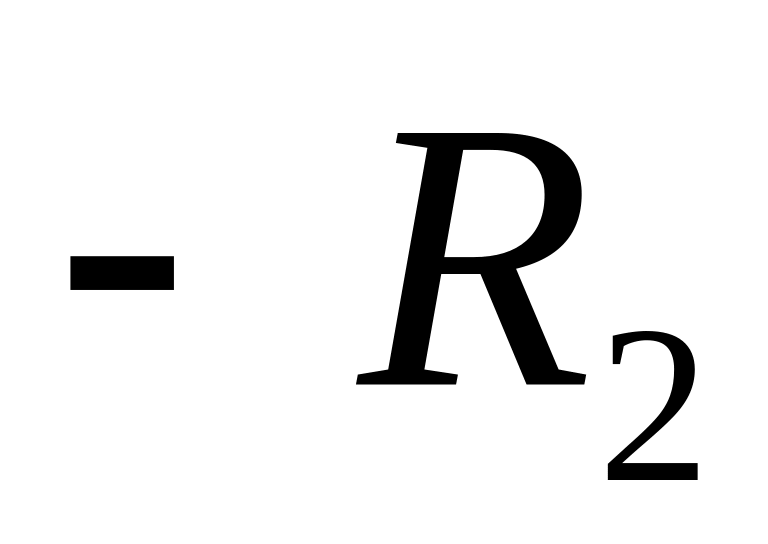
		0		1
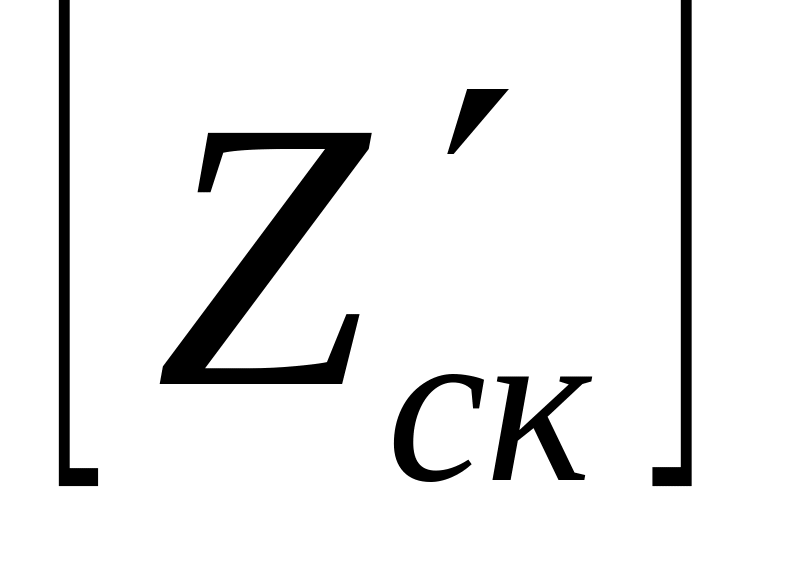=	0	0	0	2
		0		3 .

Рисунок 6.14 – Скорочена матриця опору пасивної частини схеми

2) Записуємо повну матрицю опору біполярного транзистора, як неавтономного багатополюсника, у включенні зі спільним емітером (рис. 6.15а) – у такий спосіб включені транзистори в досліджуваній схемі; для складання матриці скористаємося схемою заміщення БПТ у вигляді Т-подібної фізичної моделі (рис. 6.15б).

Рисунок 5.15 – До складання повної матриці опору БПТ

у включенні зі спільним емітером

Порядок складання повної матриці БПТ у включенні із спільним емітером такий же, як у п. 6.3.1 для включення БПТ із спільною базою: спочатку складаємо матрицю пасивної частини схеми, потім – матрицю взаємозв’язку; повна матриця БПТ формується шляхом додавання матриці пасивної частини схеми до матриці взаємозв’язку. Повні матриці опору біполярних транзисторів досліджуваної схеми, що отримані у описаний спосіб, наведені нижче. Одночасно показана їх „прив'язка” до робочої схеми підсилювача шляхом заміни номерів зовнішніх контурів транзисторів (цифри в нумерації рядків і стовпчиків матриць без дужок) номерами контурних струмів схеми, з якими співпадають ці контури – номери рядків і стовпців матриць в дужках:

	1 (1)	2 (0)	3 (2)
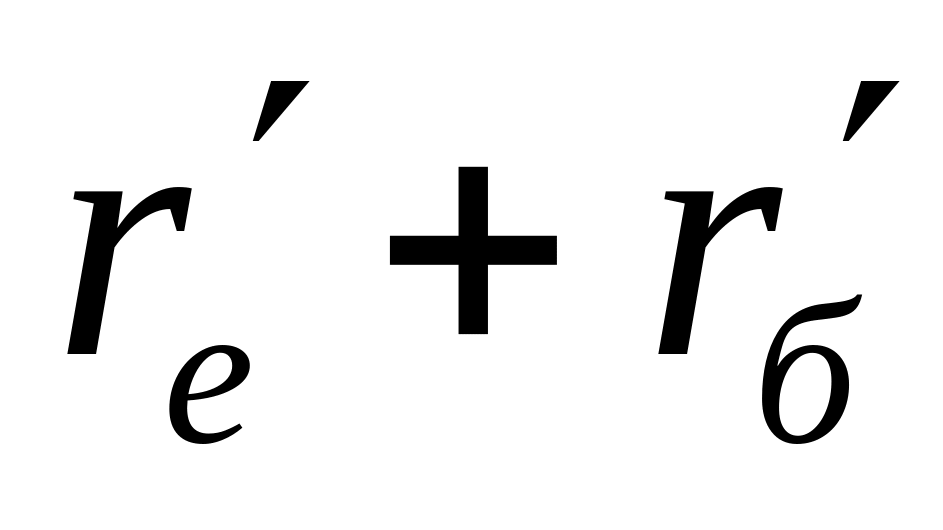
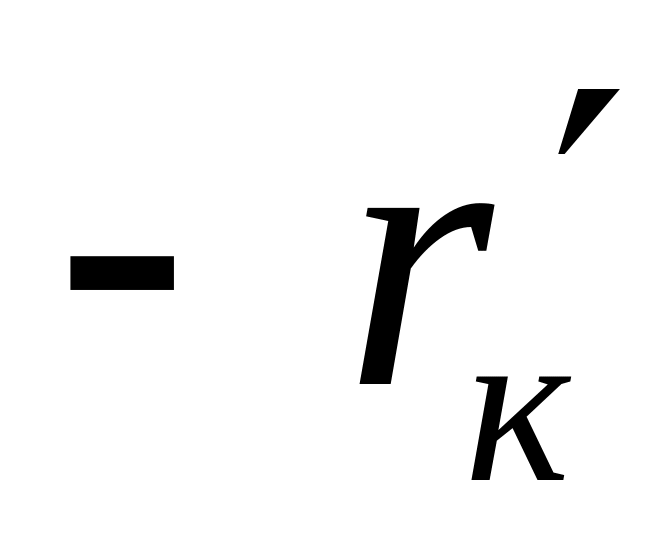
				1 (1)
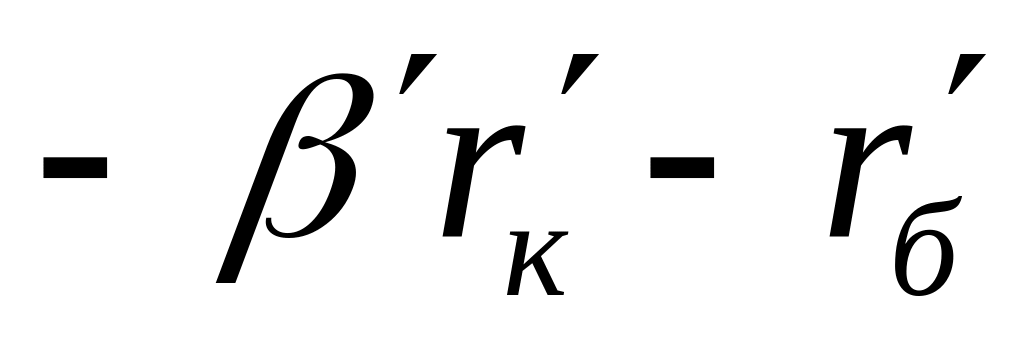
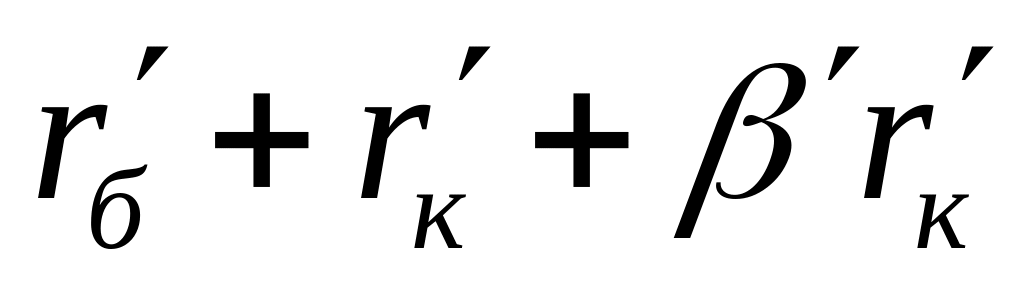
				2 (0)
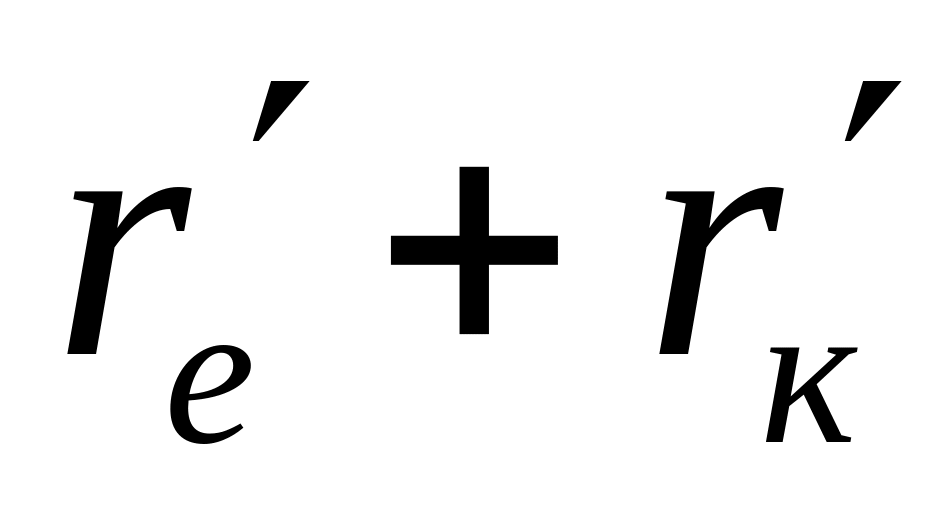
				3 (2) .

	1 (1)	2 (2)	3 (3)
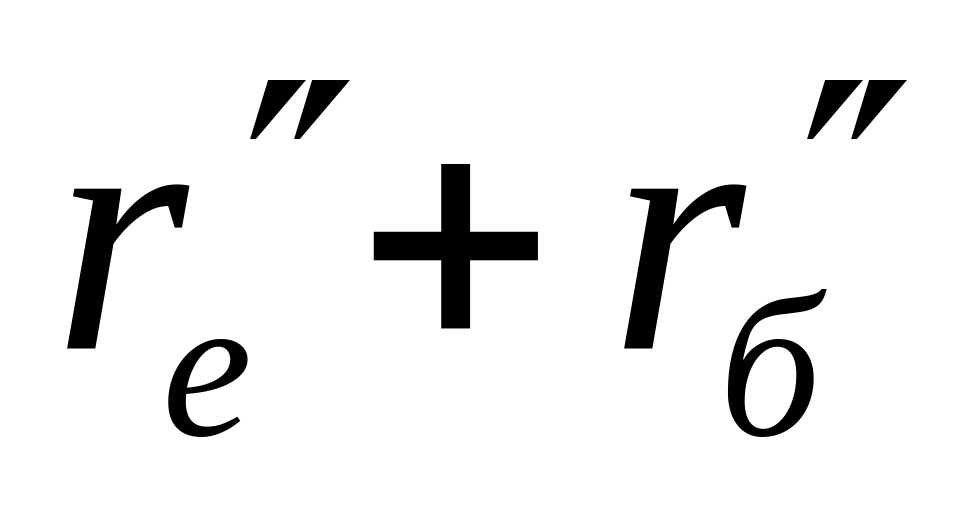
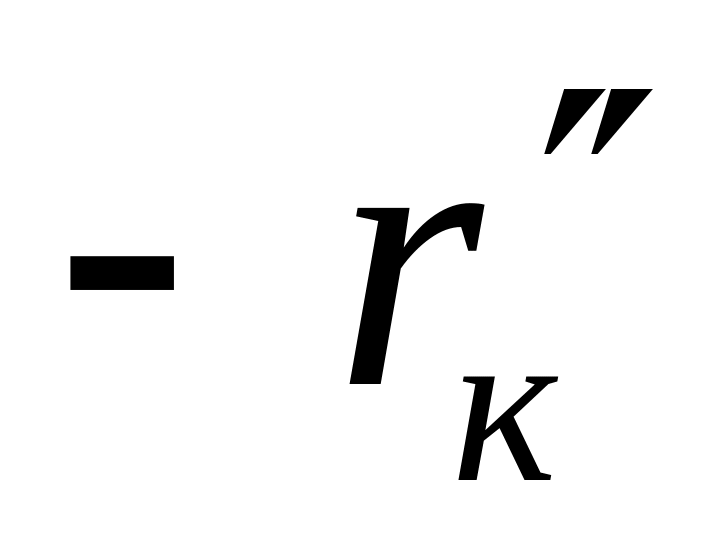
				1 (1)
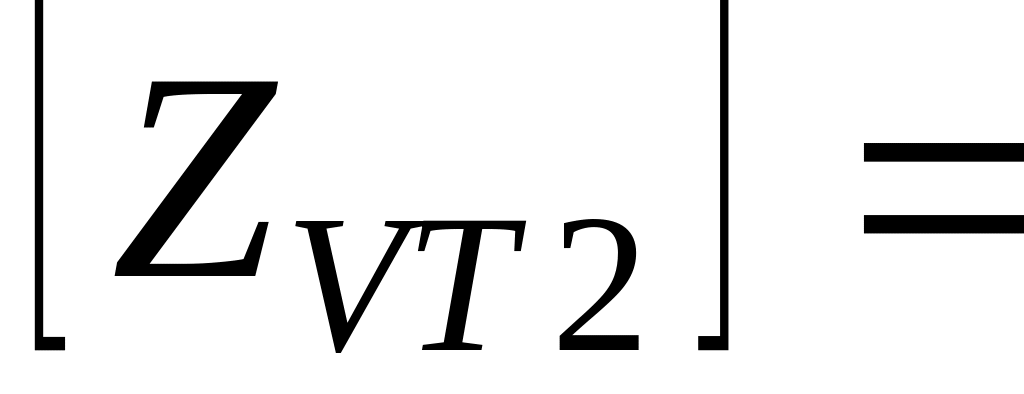
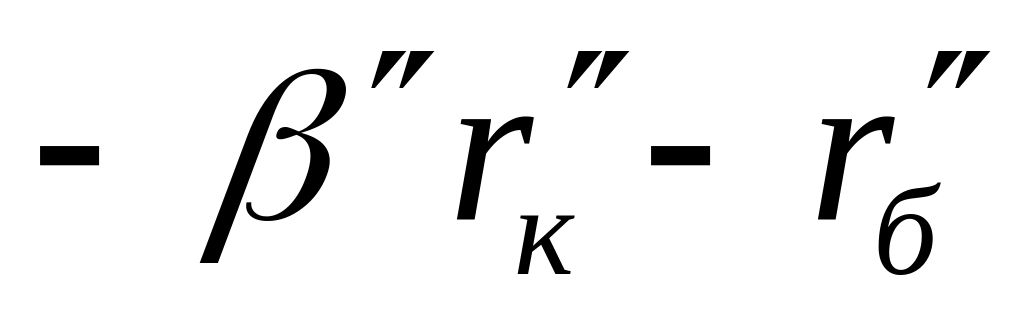
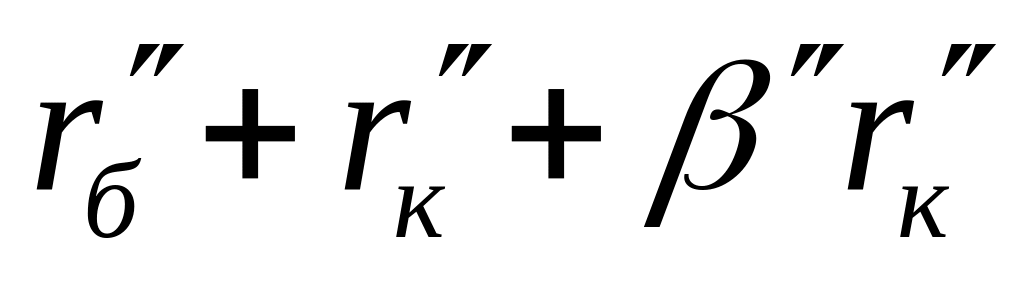
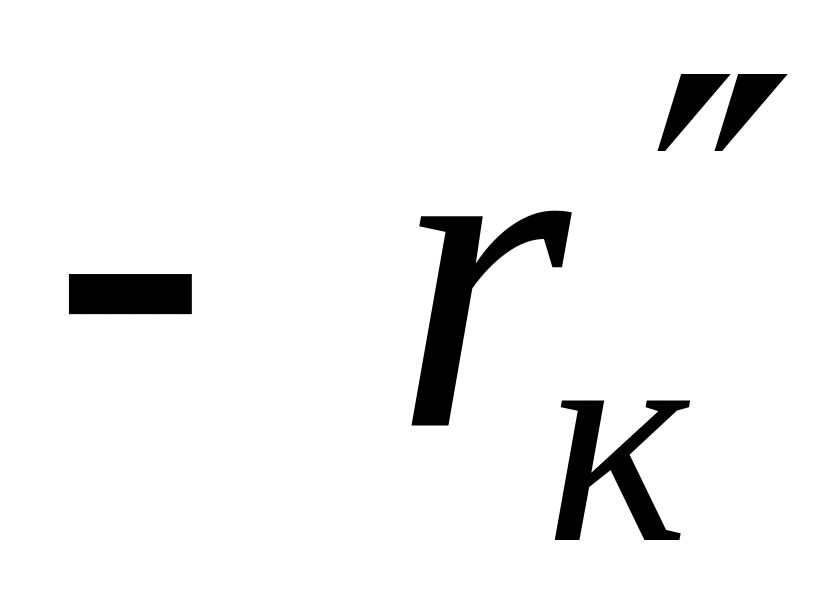
				2 (2)
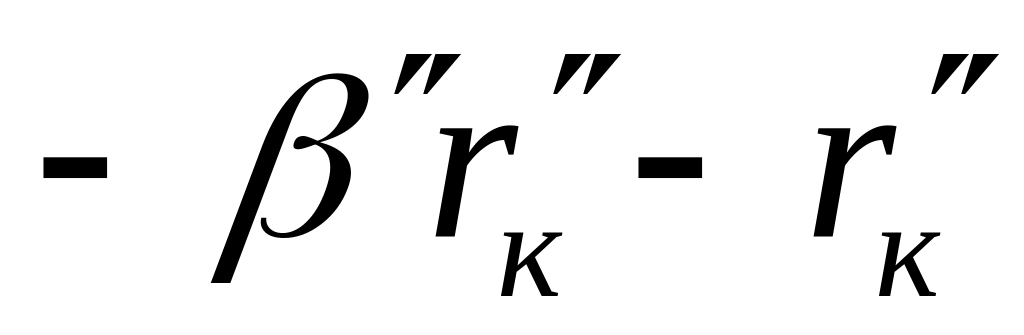
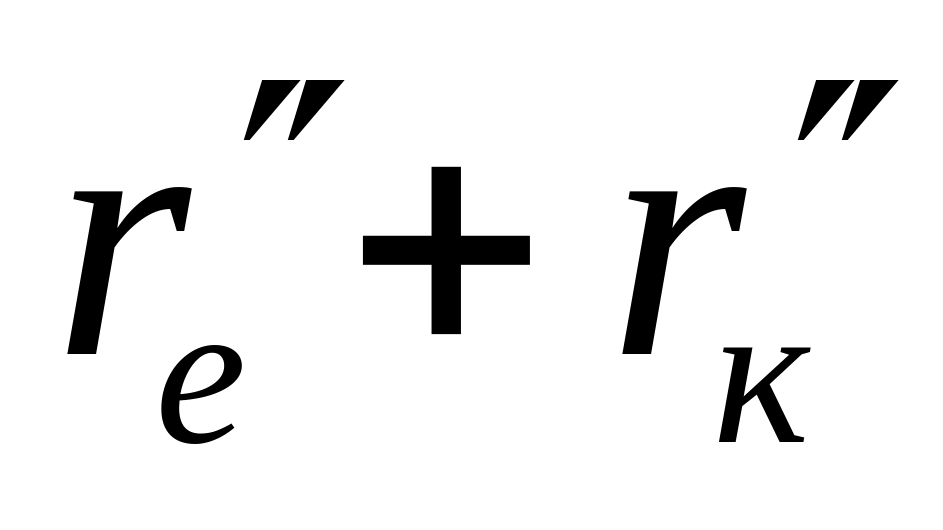
				3 (3) .

2. Скорочену матрицю опору схеми отримуємо шляхом вписування елементів повних матриць транзисторів у відповідні клітини скороченої матриці опору пасивної частини схеми (попередньо в матриці транзистора VT₁ викреслюємо 2-й рядок і 2-й стовпчик, що співпадає з базисним контуром схеми). Номера рядків і стовпців матриць транзисторів в дужках, вказують в яку клітину скороченої матриці опору пасивної частини досліджуваної схеми слід вписувати відповідний елемент повної матриці опору транзистора.

	1	2	3
				1
=				2
				3 .