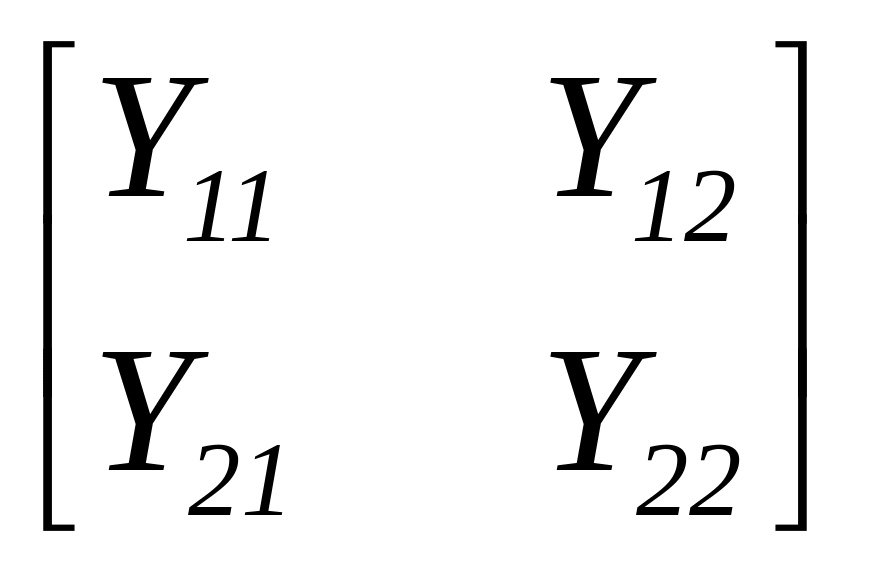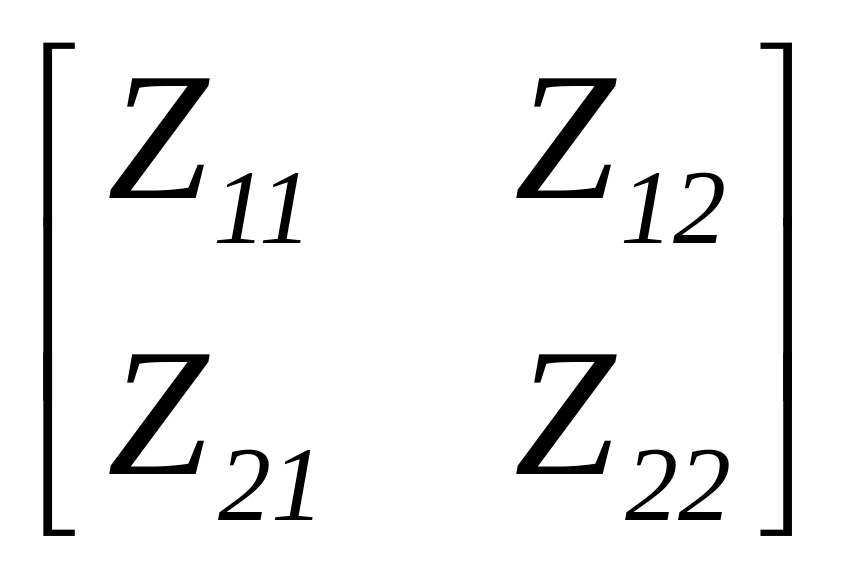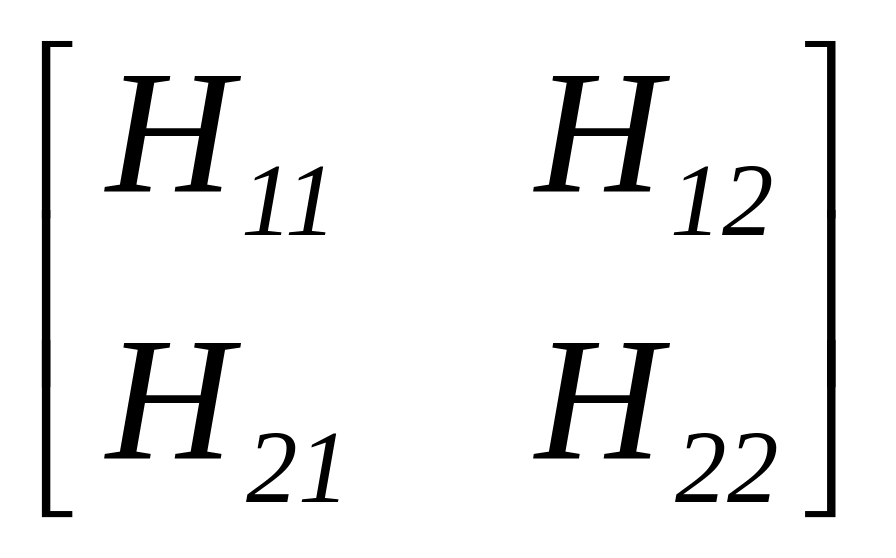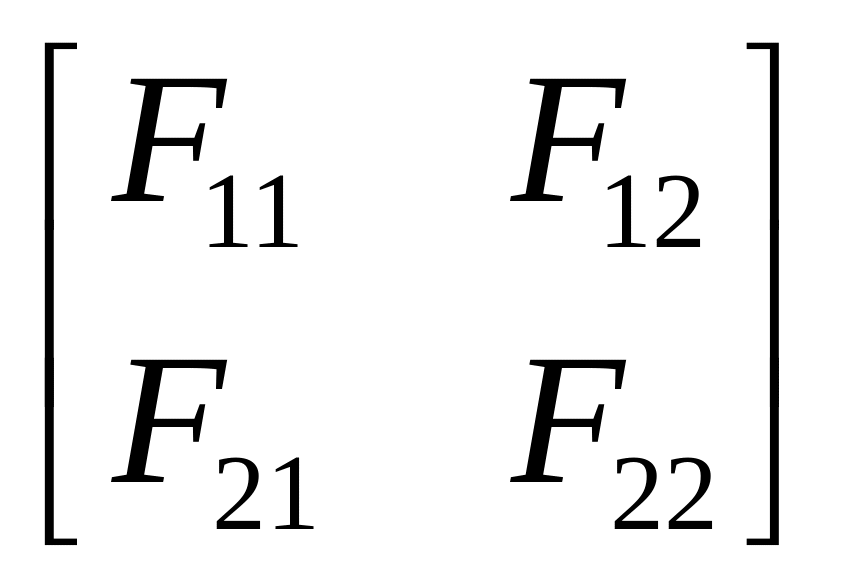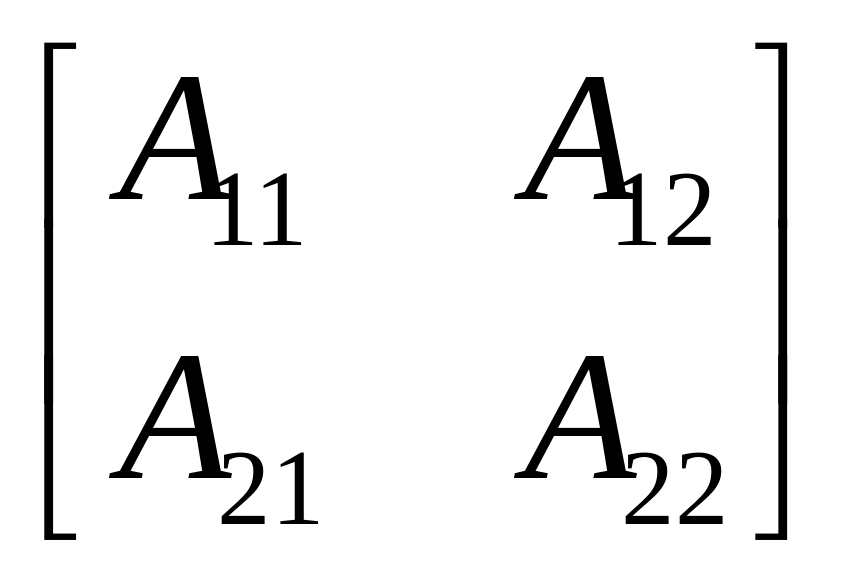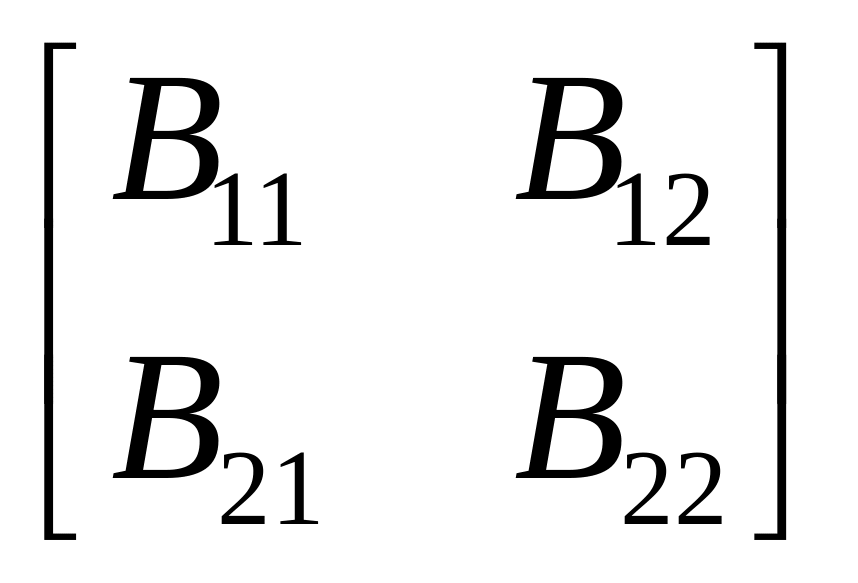26

5 Метод еквівалентного чотириполюсника

В теорії електричних кіл частину електричного кола довільної конфігурації, що має дві пари полюсів (затисків) для підключення джерела і приймача енергії (навантаження), прийнято називати чотириполюсником. В аналізі електронних схем досить часто дослідження режиму роботи складної схеми зводиться до встановлення зв'язків між струмами і напругами лише у двох гілках схеми. Кожна гілка з’єднується зі схемою за допомогою двох вузлів. Тому можна виділити частину досліджуваної схеми, що має чотири полюси (затиски), до яких підключуються названі гілки, і розглядати її як чотириполюсник, бо найчастіше до однієї пари полюсів підключується джерело енергії (сигналу) схеми, а до іншої – навантаження схеми. Перша пара полюсів вважається вхідними полюсами чотириполюсника, друга – вихідними, а сам чотириполюсник, сформований таким чином, у розрахунковому відношені - еквівалентним досліджуваній схемі.

5.1 Системи рівнянь і параметрів чотириполюсника

Будь-який чотириполюсник (рис. 5.1) можна описати рядом рівнянь, що зв'язують між собою струми і напруги на вході і виході чотириполюсника.

Рисунок 5.1 – До запису систем рівнянь чотириполюсника

Зазвичай для будь – якого чотириполюсника можна записати 6 суттєво різних пар рівнянь. Найбільше значення мають рівняння, що пов'язують вхід чотириполюсника з виходом; їх називають основними рівняннями чотириполюсника (при цьому як незалежні змінні обирають і , а як залежні - і ):

(5.1)

Рівняння, що зв'язують напруги на вході і виході чотириполюсника з відповідними струмами, записуються в наступному вигляді:

(5.2)

а рівняння, в яких за незалежні змінні приймаються напруги і - у вигляді|:

(5.3)

Так звані змішані або «гібридні» рівняння записуються наступним чином:

(5.4)

(5.5)

Нарешті, рівняння, в яких за незалежні змінні приймаються напруга і струм на вході чотириполюсника, мають вигляд:

(5.6)

У загальному випадку коефіцієнти рівнянь A, Z, Y, H, F і В є комплексними. У тих випадках, коли вони є дійсними (що має місце для більшості лінійних кіл), їх позначають малими буквами а, r (або R), g (або y), h, f і b.

Рівняння (5.1)...(5.6) можна записати у матричній формі:

;

;

;

;

;

.

У цих рівняннях квадратні матриці, як і їх елементи, є первинними параметрами чотириполюсника, що повністю його характеризують. Якщо для чотириполюсника відомі (або визначені) параметри однієї з матриць, то значення параметрів будь-якої іншої матриці цього чотириполюсника можна отримати шляхом взаємного перерахунку параметрів. У таблиці 5.1 наведено формули для взаємного перерахунку коефіцієнтів рівнянь (5.1)...(5.6) від однієї системи параметрів чотириполюсника до іншої (тут через |Y|, |Z|, |H| і т. д. позначені визначники відповідних матриць параметрів). У таблиці 5.2 наведені співвідношення між визначниками матриць еквівалентних параметрів, що дозволяють здійснювати перехід від визначника однієї системи параметрів до іншої.

Таблиця 5.1 - Залежності між параметрами чотириполюсника

від до	[Z]	[Y]	[H]
[Z]
[Y]
[H]
[А]
[F]
[B]

(продовження таблиці 5.1)

від до	[А]	[F]	[B]
[Z]
[Y]
[H]
[А]
[F]
[B]

Таблиця 5.2 - Залежності між визначниками матриць еквівалентних параметрів

від до	|Z|	|Y|	|H|	|А|	|F|	|B|
|Z|	|Z|
|Y|		|Y|
|H|			|H|
|А|				|А|
|F|					|F|
|B|						|B|

5.2 Z–параметри чотириполюсника. Визначення вторинних вихідних параметрів схеми за Z-параметрами еквівалентного чотириполюсника

Якщо як незалежні змінні обрано струми на вході і виході чотириполюсника, то для нього можна записати наступну систему рівнянь в Z-параметрах, де коефіцієнти рівнянь (параметри чотириполюсника Z₁₁, Z₁₂, Z₂₁ і Z₂₂) мають розмірність електричного опору:

(5.7)

Рівняння (5.7) дійсні при всіх значеннях незалежних змінних і . Тому вони дійсні також і у випадках, коли =0 і = 0. Припускаємо, що струм  = 0, що може мати місце коли вихідні полюси чотириполюсника розімкнені (режим холостого ходу на виході). Рівняння (5.7) при цьому набувають наступного вигляду:

Звідки отримуємо:

	-вхідний опір чотириполюсника в режимі ідеального холостого ходу його вихідного кола;
	-опір прямого зв'язку.

Відповідно, якщо припустити режим ідеального холостого ходу у вхідному колі чотириполюсника, отримаємо:

	-опір зворотного зв'язку;
	-вихідний опір чотириполюсника в режимі ідеального холостого ходу в його вхідному колі.

Приклад 5.1. Визначити Z-параметри (Z₁₁, Z₁₂, Z₂₁ і Z₂₂) чотириполюсника, схема якого наведена на рис. 5.2.

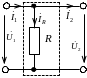
Рисунок 5.2 - Схема чотириполюсника для визначення Z-параметрів

На рис. 5.2 позначені вхідні ( ) і вихідні ( ) струми та напруги досліджуваного чотириполюсника, а також струм в резисторі R. Для наведеної схеми відповідно до прийнятих позначень можна записати, що . Тобто при (у режимі холостого ходу на виході чотириполюсника) і при (у режимі холостого ходу на вході чотириполюсника) . З урахуванням записаних співвідношень між струмами схеми в режимах холостого ходу визначаємо Z-параметри досліджуваного чотириполюсника:

а) ; в) ;

б) ; г) .

Отже, матрицю Z-параметрів досліджуваного чотириполюсника можна записати у наступному вигляді:

В аналізі електронних схем часто постає наступне завдання: треба визначити вторинні вихідні параметри досліджуваної схеми шляхом використання параметрів еквівалентного чотириполюсника, що моделює електронну схему з двома вхідними і двома вихідними затисками; при цьому до виходу чотириполюсника підключений опір навантаження Z_н, а на вході діє генератор сигналу з внутрішнім опором Z_вн (рис. 5.3):

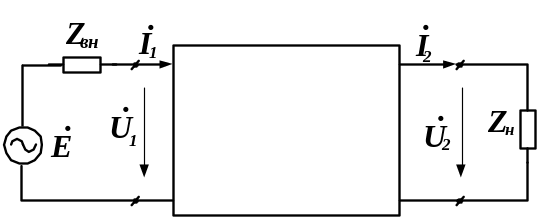
Рисунок 5.3 – Розрахункова схема до використання

еквівалентного чотириполюсника

Для вирішення цього завдання треба скласти вирази, що дозволяють визначати вторинні вихідні параметри електронної схеми із застосуванням первинних параметрів чотириполюсника, який в розрахунковому відношені є еквівалентним досліджуваній схемі. Вказані вирази можна скласти для будь-якої системи параметрів чотириполюсника; для системи Z-параметрів спосіб їх складання наведено далі.

а) Якщо в лівій частині другого рівняння системи (5.7) замінити на , отримаємо:

(5.8)

Систему (5.8) можно розвязати відносно струму :

,

звідки можна визначити вхідний опір схеми:

.

б) Якщо систему (5.8) розвязати відносно струму :

,

можна визначити провідність передачі:

,

де |Z|=det[Z_ij]=(Z₁₁Z₂₂ - Z₂₁Z₁₂ ) –визначник матриці Z-параметрів чотириполюсника.

в) Використовуючи попередній вираз для Y_пер з урахуванням можна визначити коефіцієнт передачі схеми з напруги:

.

Отримані вище залежності відомі в літературі під назвою „загального вирішення чотириполюсника за Z-параметрами”.

Аналогічним чином можна отримати ще ряд рівнянь для визначення вторинних вихідних параметрів схеми за Z-параметрами еквівалентного чотириполюсника; наприклад:

- вихідний опір чотириполюсника,

- коефіцієнт передачі зі струму, тощо.

Отже, якщо відома або будь-яким чином отримана матриця Z-параметрів чотириполюсника, що в розрахунковому відношенні є еквівалентним досліджуваній схемі, можна із застосуванням наведених вище формул визначати вторинні вихідні параметри цієї схеми.

У подібний спосіб можна скласти формули для визначення будь – яких вторинних вихідних параметрів досліджуваної електронної схеми із застосуванням будь-якої системи параметрів еквівалентного чотириполюсника. Деякі з таких формул для визначення найбільш розповсюджених (основних) вторинних вихідних параметрів підсилювальних каскадів наведено у таблиці 5.3).

Таблиця 5.3 – Формули визначення вторинних вихідних параметрів

електроннї схеми за параметрами еквівалентного чотириполюсника

Параметр	Позна- чення	Система параметрів
		[Y]	[Z]	[H]
Вхідний опір (провідність)	Wвх
Вихідний опір (провідність)	Wвих
Коефіцієнт передачі з напруги
Коефіцієнт передачі зі струму
Провідність передачі
Опір передачі

(продовження таблиці 5.3)

Позна- чення	Система параметрів		Примітки: 1. Zн – опір навантаження схе- ми. 2. Yс – внутрішня провідність джерела вхідного сигналу схеми. 3. Параметри чотириполюс- ника визначені при Yн=0 і Yс=0.
	[F]	[A]
Wвх
Wвих

ні з'єднання чотириполюсників

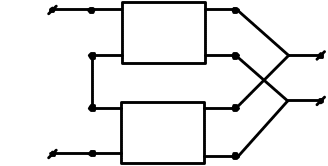
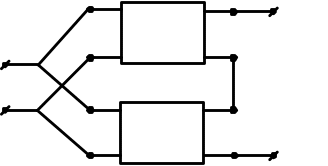
Будь-яка складна схема, що приводиться до виду чотириполюсника, може зрештою розглядатися як сполучення деяких простих (елементарних) чотириполюсників. Зазвичай, параметри таких чотириполюсників або відомі, або визначаються порівняно нескладно. При аналізі схем використовується п'ять основних видів з'єднань чотириполюсників: послідовне (каскадне), паралельне, етажне, етажно-паралельне, паралельно-етажне (дивись нижче на прикладі двох чотириполюсників).

	- Послідовне
	- Паралельне
	-Етажне
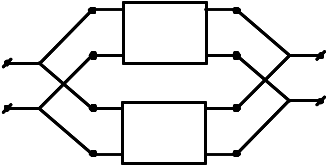
	-Етажно-паралельне
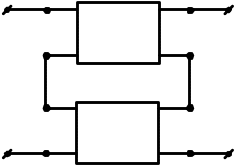
	-Паралельно-етажне

5.4 Однорідні з'єднання чотириполюсників

Якщо у складному чотириполюснику присутнє тільки одне з основних з'єднань простіших чотириполюсників (послідовне, паралельне, або інше з наведених вище), то таке сполучення простіших чотириполюсників називають однорідними. Застосування методу еквівалентного чотириполюсника базується на розв’язанні однорідних та неоднорідних з'єднань чотириполюсників. Розвязання однорідних з'єднань зводиться до визначення параметрів складного (еквівалентного) чотириполюсника за параметрами простіших, що входять до його складу і утворюють однорідне з'єднання. Формули, що дозволяють виконати розв’язання однорідних з'єднань, наведено в таблиці 5.4.

Таблиця 5.4 – Формули для розв’язання

однорідних з'єднань чотириполюсників

Сполучення	Формула
Послідовне
Паралельне
Етажне
Етажно-паралельне
Паралельно-етажне

Докажемо, наприклад, першу формулу таблиці для послідовного з'єднання чотириполюсників (рис. 5.4). Вона визначає, що: а) при однорідному послідовному з'єднанні чотириполюсників матриця А-параметрів еквівалентного чотириполюсника формується шляхом множення матриць А-параметрів послідовно сполучених чотириполюсників; б) матриці параметрів сполучених чотириполюсників перемножуються у порядку їх з'єднання.

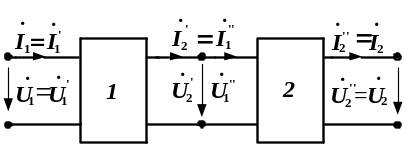
Рисунок 5.4 – Схема для аналізу послідовного з'єднання

чотириполюсників

При послідовному з'єднанні двох чотириполюсників зовнішні струми і напруги сполучених чотириполюсників і еквівалентного зв'язані між собою залежностями, що наведені на рис. 5.4. Тут: а) струми і напруги, що позначені одним штрихом, належать до першого чотириполюсника, з двома штрихами – до другого, без штрихів – до еквівалентного (складного); б) індекс „1” позначає вхідні струми і напруги всіх чотириполюсників, індекс „2” – вихідні.

Для чотириполюсників 1 і 2 можна записати наступні рівняння в системі А-параметрів:

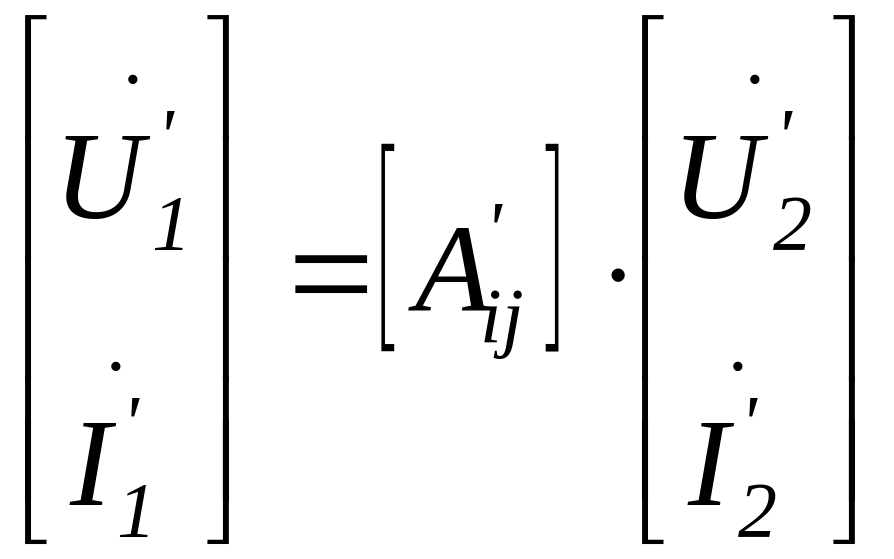і ,

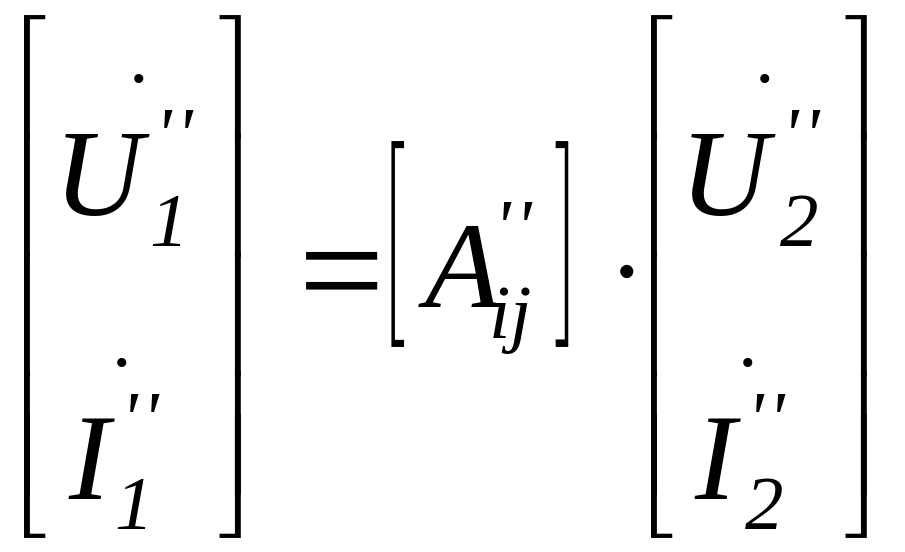де , (i=1, 2; j=1, 2) - матриця А-параметрів чотириполюсника.

Враховуючи, що:

і і ,

можна записати для еквівалентного чотириполюсника:

тобто .

Отже, із останнього рівняння видно, що матриця А-параметрів еквівалентного чотириполюсника дорівнює твору матриць А-параметрів послідовно сполучених чотириполюсників; причому, матриці А-параметрів сполучених чотириполюсників слід перемножувати в тій же послідовності, в якій вони з'єднані у складі еквівалентного. Тобто:

.

Нескладно також визначити, що при паралельному з'єднанні чотириполюсників матриця параметрів еквівалентного чотириполюсника формується шляхом сумування матриць Y-параметрів сполучених чотириполюсників (при доказі слід мати на увазі, що при паралельному з'єднанні зовнішні напруги є спільними для всіх чотириполюсників, а їх зовнішні струми сумуються).

5.5 Застосування методу еквівалентного чотириполюсника в аналізі схем

У таблиці 5.4 наведено формули для визначення матриць параметрів еквівалентного чотириполюсника, що містить однорідні з'єднання, тобто з'єднання одного виду (послідовне, паралельне, або інше з наведених вище). У загальному випадку для представлення реальної схеми (еквівалентного чотириполюсника) з'єднанням простих чотириполюсників може знадобитись не один, а декілька видів з'єднань в межах схеми. Такі з'єднання називають неоднорідними. Особливість розрахунку неоднорідних з'єднань полягає в необхідності виконання взаємних переходів від однієї системи параметрів чотириполюсника до іншої за допомогою залежностей між системами параметрів (див. розділ 5.1).

Таким чином, аналіз (розрахунок) електронної схеми за методом еквівалентного чотириполюсника зводиться до:

а) виділення в досліджуваній схемі вхідних і вихідних зажимів і представлення її еквівалентним чотириполюсником;

б) представлення еквівалентного чотириполюсника будь – яким сполученням простих чотириполюсників;

в) здобуття матриці параметрів еквівалентного чотириполюсника шляхом розвязанні однорідних та неоднорідних з'єднань чотириполюсників в межах досліджуваної схеми; відповідні матриці параметрів простих чотириполюсників, що потрібні при цьому, можна визначити або виписати із заздалегідь складених спеціальних таблиць (дивись, наприклад, наведені нижче табл. 5.5 і табл. 5.6);

г) визначення вторинних вихідних параметрів досліджуваної схеми із застосуванням параметрів еквівалентного чотириполюсника (дивись розділ 5.2).

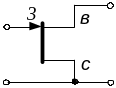
У табл. 5.5 наведено матриці параметрів польового транзистору, як чотириполюсника, для трьох способів його включення: спільний виток, спільний затвор, спільний сток (режим роботи без стумів затвору). Параметри дійсні для диапазону порівняно невисоких частот. У табл. 5.6 наведено матриці параметрів простих пасивних чотириполюсників, що досить часто застосовуються в аналізі електронних схем методом еквівалентного чотириполюсника (складаються лише з пасивних елементів).

Таблиця 5.5 - Матриці параметрів польового транзистору, як чотириполюсника

Схема	[Y]	[H]	[F]	[A]
		–
		–

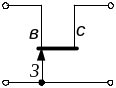
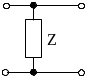
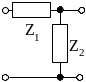
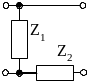
Таблица 5.6 – Матриці параметрів чотириполюсників із пасивних елементів

Схема	[Y]	[H]	[F]	[A]	[Z]
	—				—
					—
	—

Приклад 5.2. Записати матрицю параметрів чотириполюсника, еквівалентного схемі підсилювача на польових транзисторах (на рис. 5.5 наведена робоча схема підсилювача – схема для змінних складових сигналу). Вважати, що режим роботи схеми з постійного струму визначений, транзистори працюють при негативних зміщеннях на затворах в малосигнальному режимі.

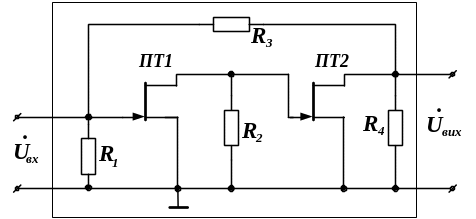
Рисунок 5.5 - Робоча схема підсилювача на польових транзисторах

Представляємо чотириполюсник, що еквівалентний досліджуваній схемі (він виділений пунктиром на рис. 5.5 ), у вигляді з'єднання простих чотириполюсників – рис. 5.6.

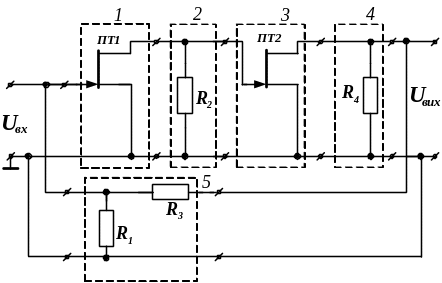
Рисунок 5.6 – Представлення еквівалентного чотириполюсника,

як з'єднання простих чотириполюсників

На рис. 5.6 чотириполюсники 1, 2, 3 і 4 сполучені послідовно; 5-й чотириполюсник – паралельно останнім. Таким чином, для подальшого розв’язання задачі потрібні матриці А-параметрів чотириполюсників 1, 2, 3 і 4, а також матриця Y-параметрів 5-го чотириполюсника. З таблиці 5.5 виписуємо матрицю А-параметрів однакових чотириполюсників „1” і „3” (польових транзисторів у включені зі спільним витоком):

і матрицю А-параметрів однакових чотириполюсників „2” і „4” з таблиці 5.6:

Визначаємо матрицю А-параметрів чотириполюсника, еквівалентного послідовно сполученим чотириполюсникам „1–4”, шляхом множення матриць А-параметрів цих чотириполюсників: [A]^(1-4)=[A]⁽¹⁾·[A]⁽²⁾·[A]⁽³⁾·[A]⁽⁴⁾. У підсумку перемноження матриць отримуємо значення параметрів А₁₁, А₁₂, А₂₁, А₂₂ шуканої матриці [A]^(1-4) для представлення її у наступному вигляді:

Для подальшого розв’язання задачі потрібна матриця [Y]^(1-4). Тому виконуємо перехід від матриці [A]^(1-4) до матриці [Y]^(1-4) цього чотириполюсника, використовуючи наступну формулу з таблиці 5.1:

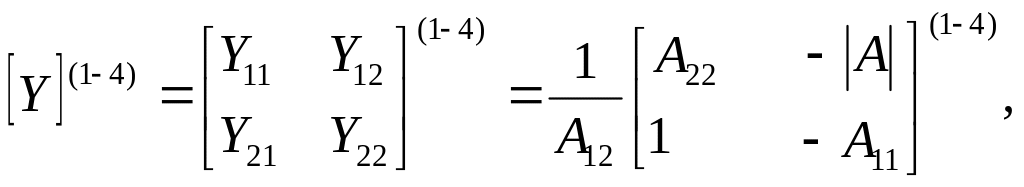
де |A|= det[A]^(1-4) = А₁₁∙А₂₂-А₁₂∙А₂₁.- визначник матриці А-параметрів.

Тепер можна записати матрицю Y-параметрів паралельно сполучених чотириполюсників „1-4” і „5”, тобто шукану матрицю Y-параметрів чотириполюсника, еквівалентного досліджуваній схемі:

[Y]=[Y]^(1-4)+[Y]⁽⁵⁾,

де - таблична матриця Y-параметрів чотириполюсника „5”.

Приклад 5.3 Користуючись методом чотириполюсника визначити коефіцієнт передачі з напруги повторювача на польовому транзисторі (схема на рис. 5.7); вважати, що повторювач працює в діапазоні частот, де реактивні опори всіх конденсаторів схеми нескінченно малі.

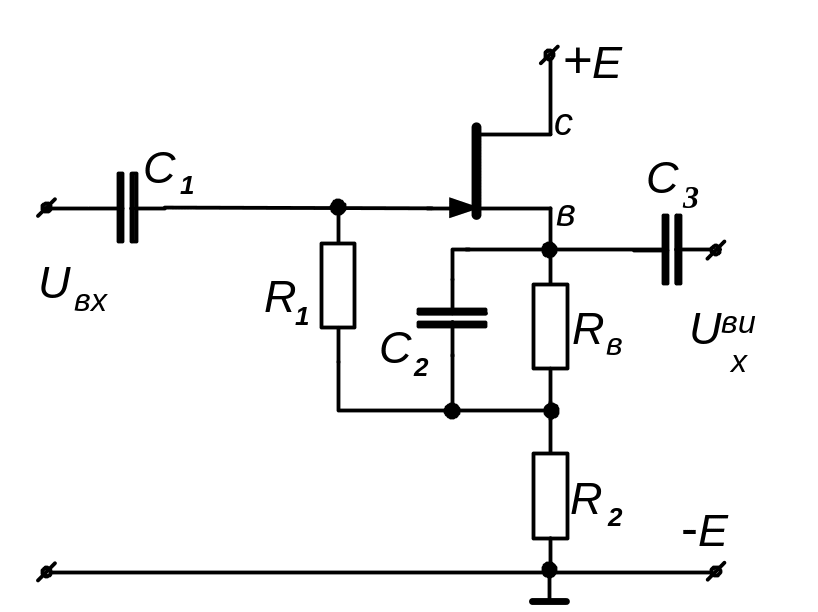
Рисунок 5.7 – Схема повторювача напруги

на польовому транзисторі

Складаємо робочу схему повторювача (рис. 5.8а) і представляємо в ній чотириполюсник, що еквівалентний досліджуваній схемі, як з'єднання простих чотириполюсників (вони виділені пунктиром на рис. 5.8б). Чотириполюсники „1” і „2” сполучені послідовно; чотириполюсник „3” підключений паралельно їм. Тому спочатку визначаємо матрицю А-параметрів чотириполюсника, що еквівалентний послідовно сполученим чотириполюсникам „1” і „2” (матрицю А-параметрів ПТ у включені зі спільним стоком виписуємо з таблиці 5.5).

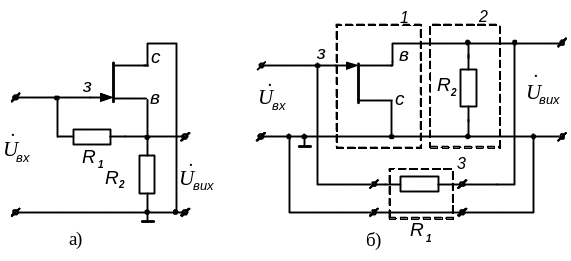
Рисунок 5.8 - Робоча схема повторювача і представлення її

з'єднанням простих чотириполюсників

,

тобто , , .

Тепер для цього чотириполюсника виконуємо перехід від матриці А-параметрів до матриці Y-параметрів (формула переходу наведена в таблиці 5.1):

.

Після того, як отримана матриця [Y]^(1,2), визначаємо матрицю Y-параметрів схеми повторювача, як паралельно сполучених чотириполюсників „1-2” і „3” (попередньо з таблиці 5.6 виписуємо матрицю Y-параметрів чотириполюсника „3”):

.

Виписуємо з таблиці 5.3 формулу для визначення коефіцієнту передачі схеми з напруги із застосуванням Y-параметрів еквівалентного чотириполюсника:

.

В схемі, наведеній на рис. 5.7, опір навантаження повторювача R_н (тобто Y_н=0). Відповідно отримуємо:

Ц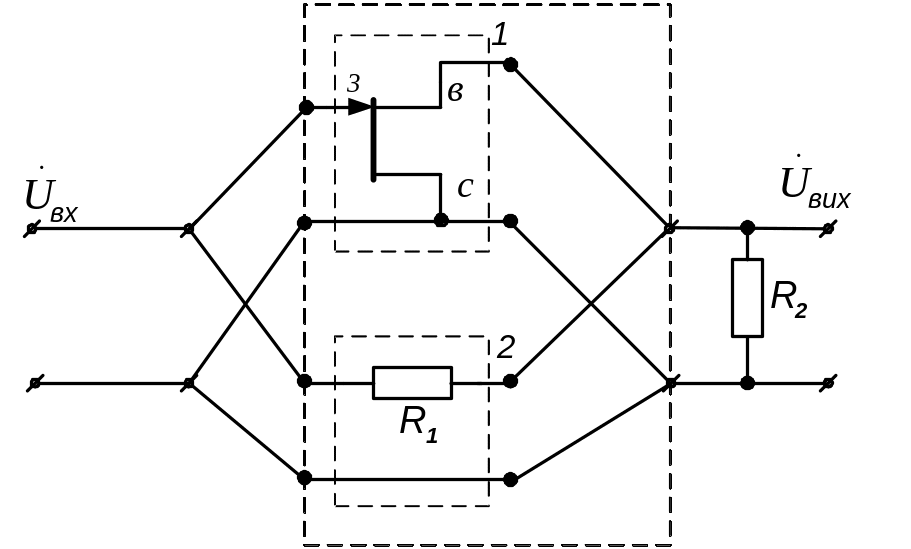 ю задачу можна розв’язати і у інший спосіб, якщо резистор R₂ вважати навантаженням еквівалентного чотириполюсника (нагадаємо, що відповідно до завдання опір навантаження повторювача R_н). При такому підході отримаємо наступну схему сполучення чотириполюсників у складі еквівалентного:

В цій схемі еквівалентний чотириполюсник містить два паралельно сполучених чотириполюсники „1” і „2”. Матрицю Y-параметрів еквівалентного чотириполюсника визначаємо наступним чином:

.

В підсумку отримуємо такий же вираз для коефіцієнта передачі схеми з напруги:

5.6 Визначення параметрів чотириполюсників

5.6.1 Параметри чотириполюсника, до виду якого приводиться електронна схема з двома вхідними і двома вихідними полюсами (затисками), можна визначити через визначник і алгебраічні доповнення матриці опору (або провідності) досліджуваної схеми. Дійсно, рівняння для зовнішніх струмів схеми, що приводиться до виду чотириполюсника, відповідно до методу контурних струмів можна записати у наступному вигляді (дивись розд. 4.5, рівняння 4.9 і 4.10):

,

,

де Δ –визначник матриці опору схеми; Δ_ba, Δ_ab, Δ_aa, Δ_bb – алгебраічні доповнення; - напруги на вході і виході схеми, відповідно.

Порівняємо наведені вище рівняння з системою рівнянь, що записані для чотириполюсника в системі Y-параметрів:

(5.9)

де , - струми на вході і виході чотириполюсника; , - напруги на вході і виході чотириполюсника, відповідно.

За умови = , = , = , = , можна записати, що:

Тобто:

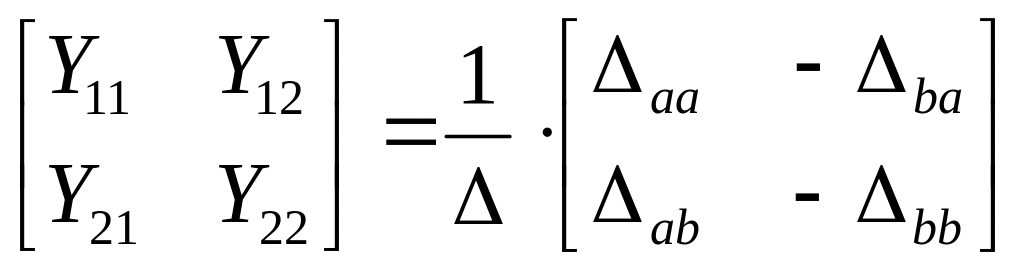. (5.10)

Таким чином, матричне рівняння (5.10) дає можливість визначати Y-параметри еквівалентного чотириполюсника шляхом використання визначника і алгебраічних доповнень матриці опору досліджуваної схеми.

Із порівняння залежностей (4.12) і (4.13), що записані для схеми з двома вхідними і двома вихідними затисками, з системою рівнянь (5.7), що записані для чотириполюсника в Z-параметрах, можна встановити що:

.

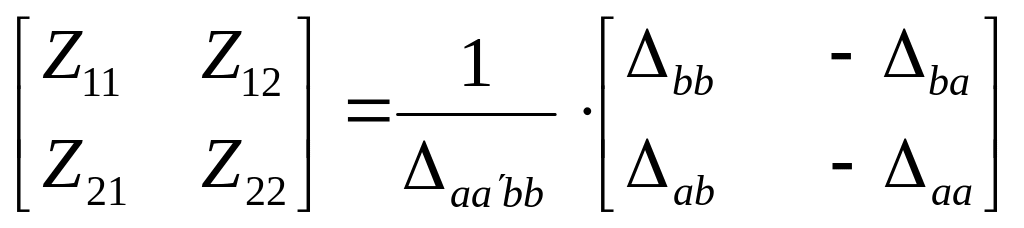Останнє рівняння дозволяє визначати Z-параметри еквівалентного чотириполюсника шляхом використання матриці опору досліджуваної схеми.

У такий же спосіб можна отримати формули для визначення і інших матриць параметрів чотириполюсника шляхом застосування як матриці опору, так і матриці провідності досліджуваної схеми (формули наведено далі в таблиці 5.7).

5.6.2 Якщо структура чотириполюсника невідома, його параметри можна визначити експериментально. Для цього необхідно по черзі на вході і виході чотириполюсника відтворити режими холостого ходу ( =0, =0) і короткого замикання ( =0, =0) і визначити відношення відповідних струмів і напруг. Якщо параметри чотириполюсника визначаються на змінному струмі, необхідно забезпечити при цьому незмінність режиму роботи чотириполюсника на постійному струмі. Режиму короткого замикання відповідає закорочування конденсатором великої ємності вхідних або вихідних зажимів чотириполюсника, а режиму холостого ходу – послідовне включення в коло відповідних зажимів котушки індуктивності. При цьому режим роботи чотириполюсника на постійному струмі не змінюється.

При експериментальному визначенні параметрів чотириполюсника слід мати на увазі наступну обставину: при відтворенні режимів холостого ходу і короткого замикання на вході чотириполюсника і подачі на його вихід задаючої напруги, струм у вихідному колі чотириполюсника (струм ) матиме напрям, протилежний прийнятому на рис. 5.1. Тому параметри чотириполюсника, що стоять коефіцієнтами при струмі в його рівняннях, будуть отримані зі знаком «мінус».

Таблиця 5.7 – Формули визначення параметрів чотириполюсника шляхом застосування визначника і алгебраічних доповнень матриці схеми

Матриця параметрів чотириполюсника	Визначення шляхом застосування
	матриці опору	матриці провідності
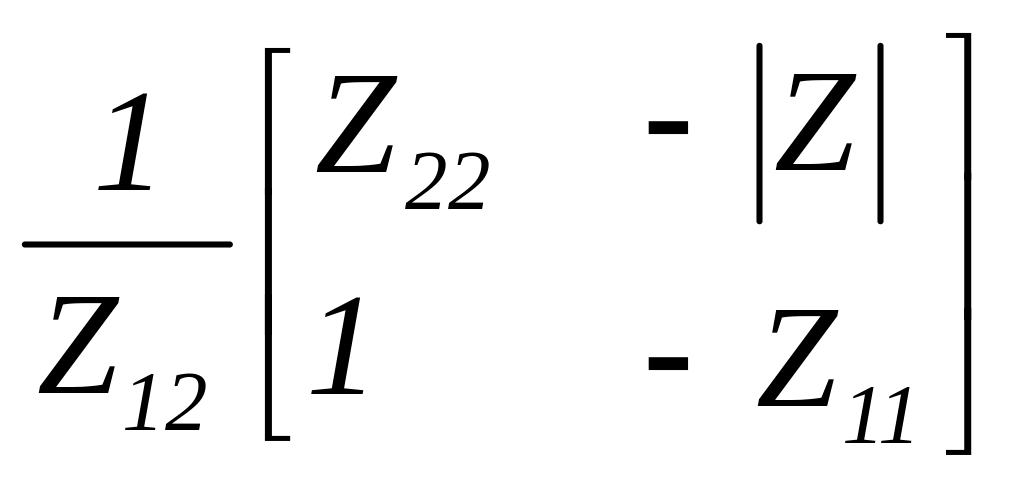
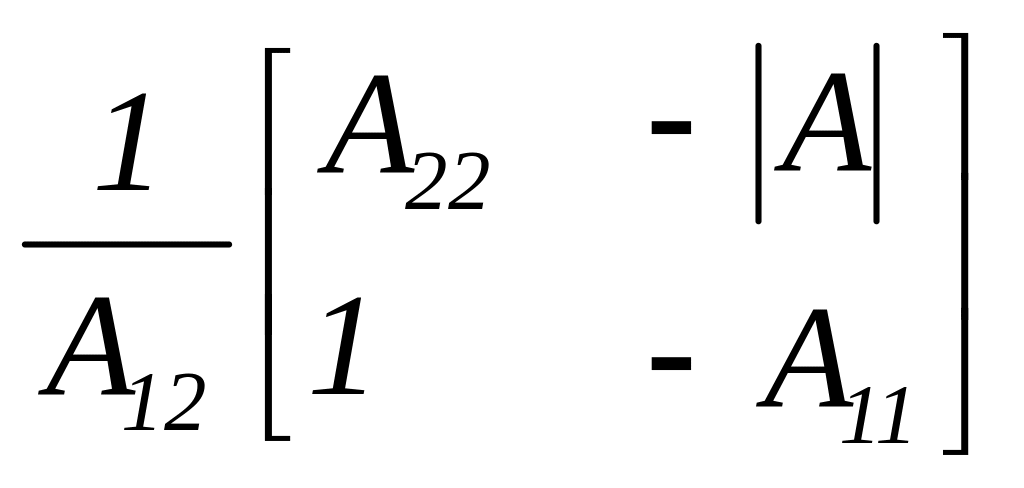
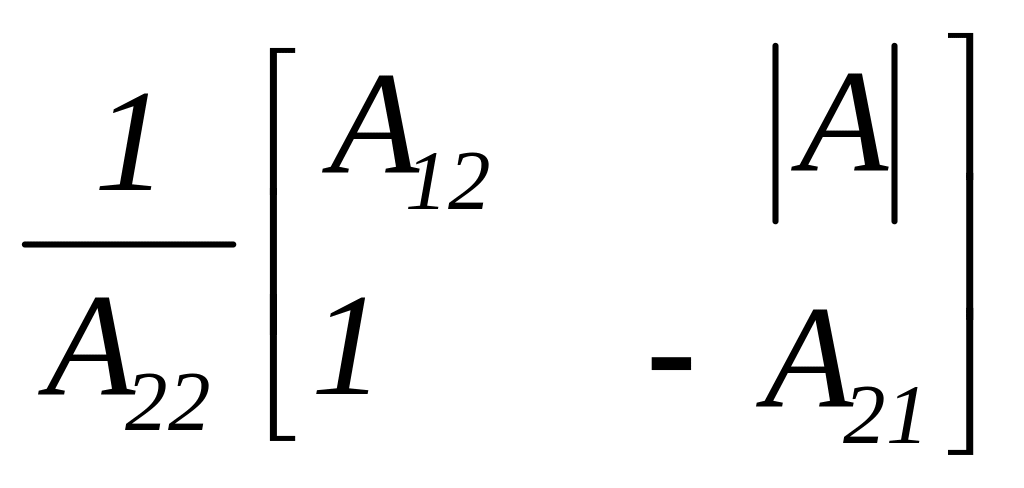
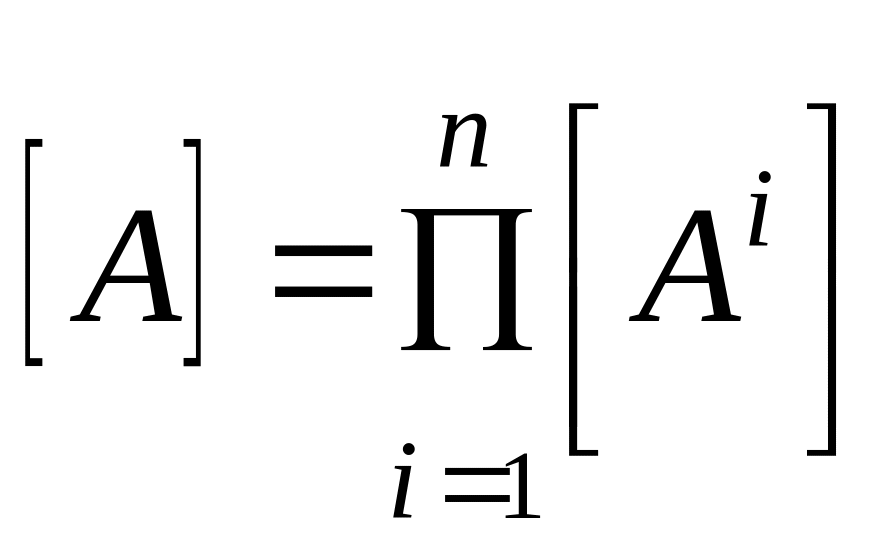
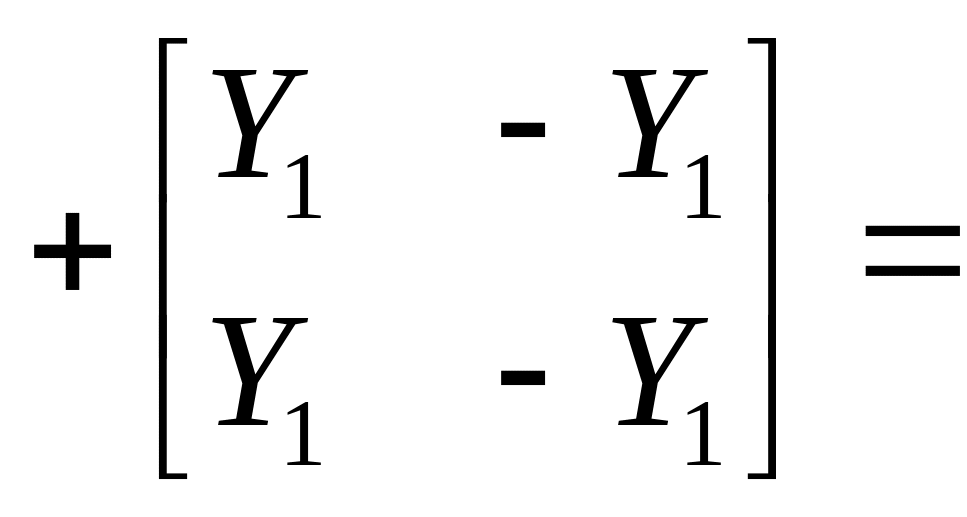
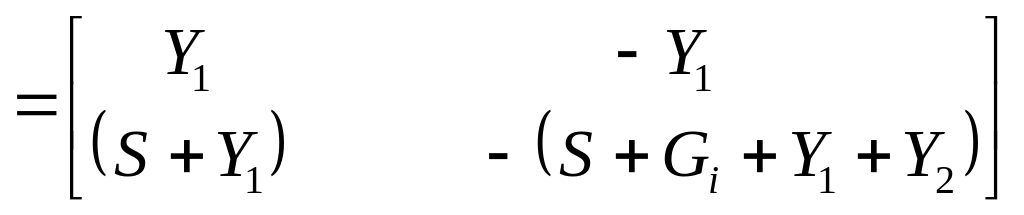