44

4 Малосигнальні методи аналізу електронних схем

4.1 Загальна характеристика малосигнальних методів

За допомогою малосигнальних методів можна визначати змінні складові струмів і напруги електронної схеми або отримувати значення вторинних вихідних параметрів досліджуваної схеми. При застосуванні малосигнальних методів вважається, що характеристики нелінійних підсилювальних компонентів електронної схеми в робочій області досить наближені до лінійних. Це обумовлено тим, що при роботі схеми в режимі перетворення малого сигналу робоча точка на характеристики підсилювального компоненту зміщується від точки спокою на незначну відстань, де нелінійність характеристик незначна. Причому, чим менше рівень сигналу в схемі, тим краще наближення характеристик до лінійних. Відповідно до цього малосигнальні методи аналізу (розрахунку) електронних схем часто називають лінійними.

При застосуванні малосигнальних методів принципова схема досліджуваного електронного кола попередньо аналізу, по можливості, спрощується – складається робоча (розрахункова) схема, що дійсна лише для режиму перетворення змінних складових сигналу (струмів, напруг, тощо). При цьому: а) внутрішні опори джерел живлення схеми приймаються такими, що дорівнюють нулю; б) залежно від частоти сигналу можна нехтувати деякими реактивними компонентами схеми (наприклад, конденсаторами на високих частотах, котушками індуктивності на низьких частотах, тощо). У зв'язку з цими спрощеннями робоча схеми досліджуваного кола в різних частотних діапазонах може приймати різний вигляд.

При складанні робочої схеми враховуються також конкретні умови роботи кола, мета і завдання аналізу. Досить часто робоча схема доповнюєтьсякомпонентами , які враховують додаткові зв'язки в схемі (паразитні ємності, індуктивні зв'язки, опори з'єднувальних дротів, опори витоку, тощо) чи побочні явища в електронних колах (шуми, завади, зміни параметрів елементів кола під дією зовнішніх чинників, тощо).

Малосигнальні методи аналізу (розрахунку) електронних схем значно простіші, ніж нелінійні методи. Вони достатньо розвинуті і багатоманітні. При проектуванні електронних пристроїв найчастіше застосовують наступні малосигнальні методи: метод еквівалентних схем, метод еквівалентного чотириполюсника, узагальнені матричні методи контурних струмів і вузлових напруг, метод орієнтованих графів.

Найчастіше при аналізі чи розрахунку простих підсилювальних схем, що працюють в малосигнальному режимі, використовують метод еквівалентних схем. Він заснований на заміні підсилювального елементу електронного кола (біполярного або польового транзистора, операційного підсилювача, оптрона, вакуумного прилада, тощо) еквівалентною схемою (схемою заміщення, лінійною моделлю), що складається з двополюсних пасивних компонентів і керованих (залежних) джерел струму або напруги. Після цього формально задача зводиться до аналізу електричного кола із двохполюсними елементами за допомогою апарату теорії лінійних електричних кіл (законів Кирхгофа, методу контурних струмів, методу вузлових напруг, тощо). Із застосуванням методу еквівалентних схем можна отримати аналітичні вирази для розрахунку вторинних вихідних параметрів схеми за відомими параметрами елементів еквівалентної схеми, досліджувати частотні залежності і часові характиристики схеми, тощо. Але цей метод зручний для аналізу лише простих схем. З ускладненням схеми застосування методу обмежено громіздкістю отриманих аналітичних виразів і складністю їх застосування при аналізі чи розрахунках. Крім того, при виконанні аналізу різних підсилювальних схем потрібно кожного разу представляти їх еквівалентними схемами. І якщо для простих схем цей недолік майже не відчувається, то із ускладненням схеми виникають труднощі при переході від реальної схеми до її еквіваленту (особливо це стосується схем із зворотними зв'язками).

Метод еквівалентного чотириполюсника (далі – метод чотириполюсника) заснований на представленні складної підсилювальної схеми з двома вхідними і двома вихідними полюсами (затисками) у вигляді деякого еквівалентного чотириполюсника. Причому сам чотириполюсник в процесі аналізу заміщується деяким з'єднанням простіших чотирьохполюсників, параметри яких вважаються відомими або легко визначаються. Гідність методу полягає в тому, що при його використанні немає потреби у застосуванні еквівалентних схем заміщення підсилювальних компонентів схеми. Застосування математичного апарату матричної алгебри дозволяє значно спростити розрахунки в порівнянні з методом еквівалентних схем, формалізувати розрахунки, що вельми важливо для машинних методів аналізу. При застосуванні методу можна використовувати заздалегідь складені таблиці параметрів простих (елементарних) чотириполюсників, що є в літературі, а параметри всієї схеми визначити за відповідними формулами в залежності від способу з'єднання цих чотириполюсників.

Не дивлячись на значні гідності, метод чотириполюсника має ряд недоліків. Основний з них - вимога регулярності з'єднання простих (елементарних) чотирьохполюсників у складі досліджуваної схеми. Нерегулярність же з'єднань особливо часто з'являється в схемах із зворотними зв'язками, що запроваджуються в схемі свідомо або що виникають за рахунок паразитних зв'язків між окремими каскадами. І хоч для аналізу і розрахунку підсилювачів із нерегулярними з'єднаннями була розроблена теорія чотириполюсника з трьома сторонами, однак із-за складності її майже не застосовують.

Узагальнені матричні методи вузлових напруг і контурних струмів дозволяють отримувати повну матрицю (електричної провідності або опору) досліджуваної схеми безпосередньо із розгляду робочої схеми без заміщення її еквівалентною схемою. Шукані струми чи напруги, або вторинні вихідні параметри схеми надалі визначають із застосуванням матриці електричного опору або електричної провідності досліджуваної схеми. При застосуванні методу теж можна використовувати заздалегідь складені таблиці матриць неавтономних багатополюсників електронних схем (вони є в літературі), що значно спрощує аналіз.

Метод орієнтованих (сигнальних) графів використовується для адекватного представлення досліджуваної електронної схеми деякою топологічною структурою. Граф складається з деякої сукупності вершин і направлених гілок. Перехід від початкової (робочої) схеми до її графа здійснюється на основі рівнянь компонентів схеми і залежностей між струмами і напругами аналізуємої схеми. Функції схеми, що цікавлять, отримують або шляхом застосування формули передачі графа, або послідовним перетворенням графа до еквівалентної гілки.

4.2 Метод еквівалентних схем

Суть методу еквівалентних схем полягає у відображенні реальних електронних кіл еквівалентними в розрахунковому відношенні електричними схемами на ідеальних двополюсних компонентах. При цьому виявляється можливим розповсюдити на електронні кола методи розрахунку електричних кіл. При переході від реальної схеми до еквівалентної при відображенні підсилювальних елементів електронних кіл їх мало сигнальними моделями виникає поняття керованого джерела струму або напруги. Саме введення керованого (залежного) активного елементу (джерела) разом з незалежними пасивними двополюсниками і дозволило певною мірою розповсюдити класичні методи електротехніки на електронні кола.

Послідовність операцій з використання методу еквівалентних схем для аналізу чи розрахунку електронних схем зводиться до наступного:

1) у робочій (розрахунковій) схемі, що дійсна лише для змінних складових струмів і напруг, замінюють підсилювальні компоненти їх еквівалентними схемами (схемами заміщення, лінійними моделями); розглядаючи виводи підсилювального елементу по черзі, з'єднують відповідні виводи цієї еквівалентної схеми з тими ж елементами, що і у робочій схемі;

2) вибирається сукупність незалежних струмів і напруг і яким-небудь чином складаються рівняння для еквівалентної схеми досліджуваного кола (найчастіше застосовують методи контурних струмів або вузлових напруг, рідше – закони Кирхгофа);

3) в схемах заміщення підсилювальних елементів кола замінюють струм (напругу), що керує залежним джерелом, струмами (напругами) еквівалентної схеми, що обрані у якості незалежних при складанні рівнянь;

4) залежно від завдання аналізу виділяють в еквівалентній схемі досліджуваного кола визначальні струми і (або) напруги – тобто ті струми і напруги, із застосуванням яких визначаються шукані вторинні вихідні параметри схеми;

5) вирази для струмів (напруг), що керують, отримані у п. 3, підставляють в рівняння еквівалентної схеми, які розв'язують відносно визначальних струмів і напруг;

6) на підставі співвідношень для визначальних струмів і напруг складають вирази для визначення шуканих вторинних вихідних параметрів досліджуваної схеми.

Слід зауважити наступне: якщо аналіз чи розрахунок електронного кола планується виконувати (п. 2) із застосуванням його еквівалентної схеми методом контурних струмів, то в еквівалентній схемі (п. 1) слід використовувати моделі підсилювальних елементів з керованими джерелами напруги. При застосуванні ж методу вузлових напруг має сенс використовувати моделі з керованими джерелами струму.

Приклад 4.1. Визначити основні параметри транзисторного підсилювального каскаду за схемою зі спільною базою (CБ). Схема підсилювача наведена на рис. 4.1. Вважати, що режим роботи підсилювача за постійного струму визначений, схема працює в режимі підсилення змінних сигналів малого рівня; частота вхідного сигналу мала і параметри транзистора – дійсні числа.

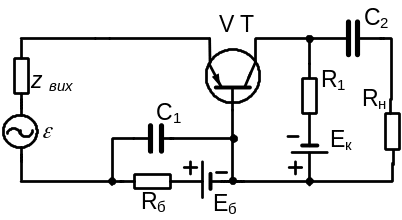
Рисунок 4.1 – Cхема транзисторного підсилювального каскаду

за схемою зі спільною базою

При формуванні розрахункової (робочої) схеми підсилювача в наближенні змінних складових струмів і напруг вважаємо, що: а) на частоті підсилюваного сигналу внутрішні опори джерел живлення схеми E_к і E_Б дорівнюють нулю і в робочій схемі виводи кожного з них з’єднуємо перемичками; б) конденсатор С₁ має достатньо велику емність, його реактивний опір нескінченно малий у порівнянні з опором резистора R_Б (X₁<<R_Б ) і його виводи з’єднуємо перемичкою; в) ємність конденсатора С₂ невелика, його реактивний опір зрівняний з опором R_Н і С₂ залишаємо в робочій схемі. З врахуванням цього викреслюємо робочу (розрахункову) схему підсилювача, що дійсна лише для змінних складових струмів і напруг (рис. 4.2):

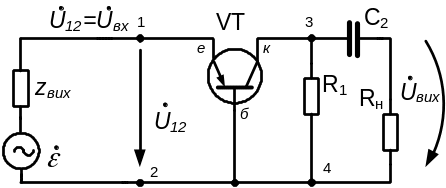
Рисунок 4.2 – Робоча схема підсилювального каскаду

Для побудови еквівалентної схеми підсилювача скористаємося Т-подібною фізичною моделлю транзистора у включені зі спільною базою з керованим джерелом напруги (рис. 4.3):

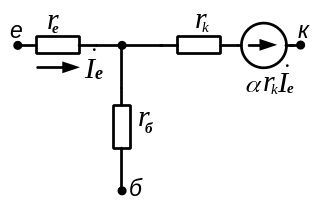
Рисунок 4.3 - Фізична малосигнальна модель транзистора

В робочій схемі підсилювача, що наведена на рис. 4.2, замінюємо біполярний транзистор його малосигнальною моделлю (рис. 4.3) і отримуємо еквівалентну схему підсилювача (рис. 4.4). Ця схема в подальшому застосовується для визначення параметрів досліджуваного підсилювального каскаду.

Рисунок 4.4 - Еквівалентна схема підсилювача

Позначаємо навантаження підсилювача відносно т.3 і 4 (R₁, R_н и С₂) як z_н. Вважаємо, що вхідна напруга підсилювача відома, і складаємо рівняння для даної схеми за методом контурних струмів. Струм 1-го контура ( ) приймаємо співпадаючим із струмом , що керує джерелом . Оскільки = , то . Напрям струму приймаємо відповідно до напряму дії керованого джерела. Таким чином отримуємо наступну систему рівнянь:

(4.1)

(4.2)

Застосовуємо складену систему рівнянь для визначення основних параметрів підсилювального каскаду.

а) Рівняння (4.2) записуємо у вигляді:

.

З останнього рівняння визначаємо коефіцієнт передачі транзистора зі струму в схемі досліджуваного підсилювача (СБ):

У загальному випадку , оскільки чисельник менше знаменника. Зазвичай r_б<<r_k; якщо можна нехтувати Z_н порівняно з r_к, то .

б) Із схеми, наведеної на рис. 4.4, видно, що

Якщо поділити на , то можна отримати коефіцієнт передачі підсилювача зі струму відносно опору навантаження:

в) З рівняння (4.2) визначаємо струм :

_,

і підставляємо цей вираз в (4.1):

. (4.3)

Із останнього рівняння можна визначити вхідний опір схеми:

(4.4)

Аналіз формули (4.4) дає наступне: r_k – для малопотужних транзисторів має порядок декілька кОм; r_б – для малопотужних транзисторів має порядок декілька десятків Ом; r_е – для малопотужних транзисторів має порядок декілька сотень Ом або декілька кОм; Z_н – має порядок кОм. Тобто вхідний опір підсилювального каскаду за схемою із спільною базою малий і має порядок величини r_э.

_{г) Враховуючи, що і можна отримати} формулу для визначення коефіцієнта передачі каскада з напруги:

(4.5)

Аналіз формули (4.5) показує, що при чималому значенні Z_н , тобто великих значеннях R₁ і R_н, коефіцієнт передачі з напруги може бути значно більше 1. В диапазоні частот, де впливом ємності С₂ можна нехтувати, - число дійсне і позитивне, більше 1 (тобто даний каскад не змінює фазу вхідного сигналу).

Таким чином, каскад із спільною базою характеризується: а) малим значенням вхідного опору; б) коефіцієнтом передачі зі струму, що менше 1; в) при правильному виборі опорів резисторів в колі колектора коефіцієнт передачі з напруги може бути значно більше 1; г) каскад може забезпечити значне посилення з потужності.

Приклад 4.2. Скласти еквівалентну схему підсилювального каскаду на біполярному транзисторі (БПТ), виконаного за схемою зі спільним емітером (СЕ), для визначення його малосигнальних параметрів. Використати малосигнальну модель БПТ в h-параметрах. Схема підсилювача наведена на рис. 4.5.

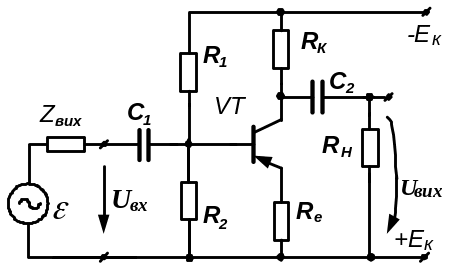
Рисунок 4.5 - Схема підсилювального каскаду на БПТ за схемою

зі спільним емітером

Складаємо робочу схему підсилювального каскаду - рис. 4.6:

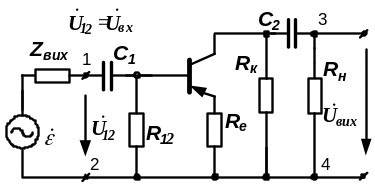
Рисунок 4.6 - Робоча (розрахункова) схема підсилювального каскаду

Малосигнальна модель БПТ в h-параметрах у включені зі спільним емітером має наступний вигляд:

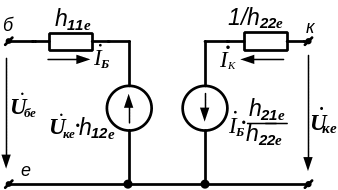
Рисунок 4.7 - Малосигнальна модель БПТ

На підставі робочої схеми (рис. 4.6), використовуючи модель БПТ (рис. 4.7), викреслюємо еквівалентну схему каскаду (рис. 4.8):

Рисунок 4.8 - Еквівалентна схема підсилювального каскаду

Приклад 4.3. Скласти еквівалентну схему витокового повторювача напруги на польовому транзисторі (ПТ), що працює в режимі посилення малого сигналу. Схема повторювача наведена на рис. 4.9.

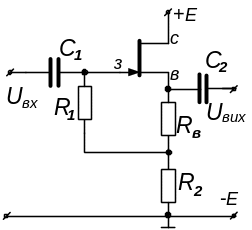
Рисунок 4.9 – Принципова схема витокового повторювача напруги

Складаємо робочу схему підсилювального каскаду – схему для змінних складових сигналу (вважаємо при цьому, що ємності конденсаторів достатньо великі і реактивні опори їх нескінченно малі).

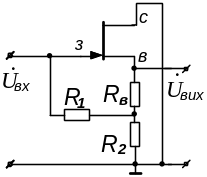
Рисунок 4.10 –Робоча схема витокового повторювача напруги

Замінюємо в робочій схемі польовий транзистор його малосигнальною моделлю з керованим джерелом напруги і внутрішнім опором R_i і отримуємо шукану еквівалентну схему витокового повторювача напруги на польовому транзисторі – рис. 4.11.

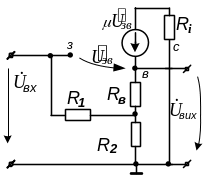
Рисунок 4.11 – Еквівалентна схема витокового повторювача напруги

на основі моделі ПТ з керованим джерелом напруги .

4.3 Вторинні вихідні параметри підсилювальних каскадів

В аналізі електронних підсилювальних каскадів найчастіше представляють інтерес не струми і напруги в схемі, а співвідношення між ними на вході і виході схеми. Ці співвідношення в узагальненому вигляді виражаються деякими функціями комплексної змінної p=+j і називаються функціями схеми або вторинними вихідними параметрами схеми.

Нехай до підсилювальної схеми з двома вхідними і двома вихідними затисками (полюсами) підключені, відповідно, джерело енергії (або сигналу) і опір навантаження. Джерело вхідного сигналу може бути представлено у вигляді генератора напруги з е.р.с. Е і внутрішнім опором Z_u (рис. 4.12а) або генератора струму J з внутрішньою провідністю Y_u (рис. 4.12б). Навантаження схеми може бути представлено опором Z_н (рис. 4.12а) або провідністю Y_н (рис. 4.12б). Причому, для схеми, наведеної на рис. 4.12а, можна записати:

а для схеми на рис. 4.12б:

Рисунок 4.12 – Схеми підключення джерела сигналу та опору навантаження

до підсилювального каскаду

Важливими вторинними вихідними параметрами підсилювальних схеми, що характеризують передачу сигналу (або енергії), є наступні:

	- коефіцієнт передачі з напруги;
	- коефіцієнт передачі зі струму;
	- опір передачі;
	- провідність передачі.

Опір і провідність передачі можна визначити через інші вторинні вихідні параметри схеми:

До важливих вторинних вихідних параметрів відносять також:

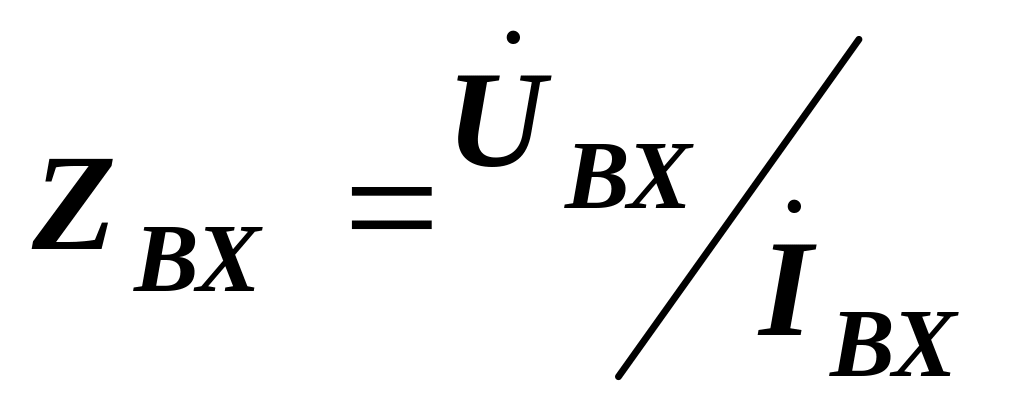
	-вхідний опір схеми;
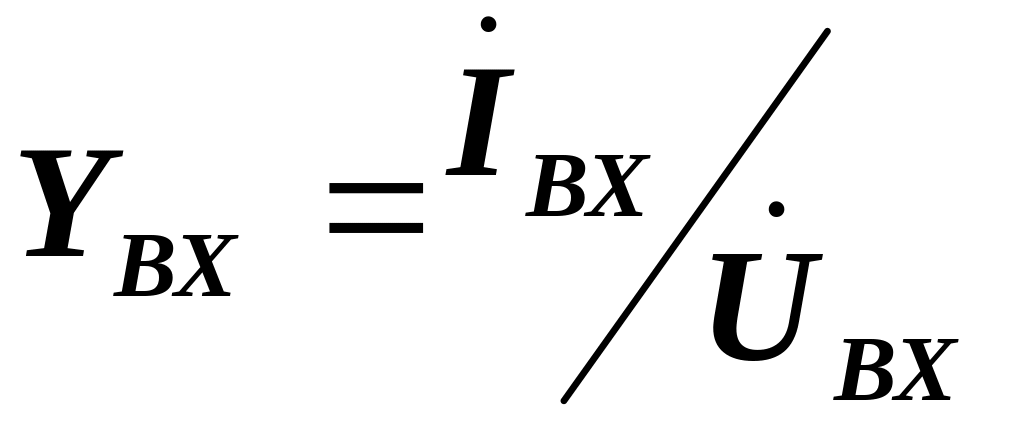
	-вхідну провідність.

Вхідні опір і провідність також можна визначити через інші вторинні вихідні параметри схеми:

Вхідний опір або вхідна провідність характеризують схему, як навантаження на джерело вхідного сигналу.

Підсилювальний каскад разом з джерелом вхідного сигналу відносно вихідних зажимів відповідно до теореми про еквівалентний генератор можна представити еквівалентним генератором напруги або еквівалентним генератора струму. При цьому е.р.с. еквівалентного генератора (рис. 4.13а) визначається як вихідна напруга каскаду в режимі х.х., а струм еквівалентного генератора (рис. 4.13б) – як струм в режимі к.з. на виході каскада. Вихідний опір (провідність) еквівалентного генератора визначається як вхідний опір (провідність) підсилювального каскаду відносно затисків підключення до нього опору (провідності) навантаження.

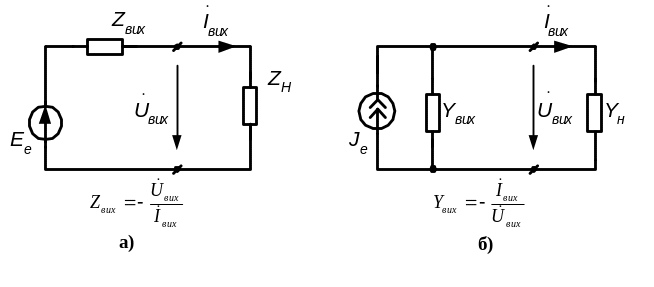
Рисунок 4.13 – Схеми заміщення підсилювального каскаду еквівалентним

генератором напруги (а) і струму (б)