3.4 Визначення реакції нелінійного резистивного кола за відомою

характеристикою кола і заданим вхідним сигналом

Для визначення реакції кола за його відомою характеристикою і заданим сигналом на вході найчастіше застосовують один з методів- графічний або аналітичний.

Суть графічного методу визначення реакції f₂(t) по заданому сигналу на вході кола f₁(t) і відомій характеристиці НРК зрозуміла із рис. 3.2. Тут зображена характеристика кола – графік залежності вихідної реакції f₂ від діючого на вході сигналу f₁, побудовані залежності від часу заданого сигналу f₁ (внизу) і шуканої реакції кола f₂ (справа). Для простоти форма вхідного сигналу прийнята гармонійною. Для отримання необхідної точності аналізу при побудові слід використати достатньо велику кількість точок, особливо в тих місцях, де характеристика кола або вхідний сигнал мають ділянки з великою крутизною. Недоліки побудов, наведених на рис. 3.2, полягають у тому, що діючий сигнал і шукана реакція розташовуються в різних місцях креслення, що утрудняє їх порівняння. Зручніше розташовувати графіки f₁(t) і f₂(t) один під одним, як це зроблено на рис. 3.3.

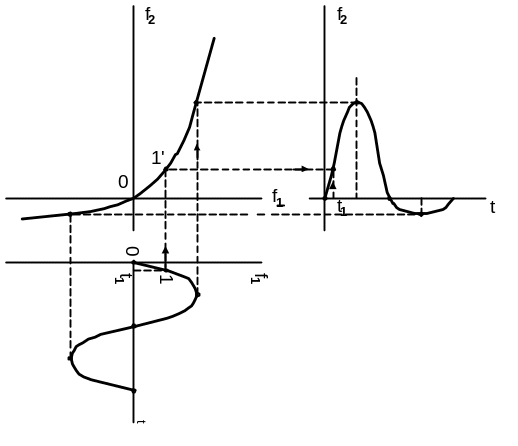
Рисунок 3.2 – Визначення реакції НРК графічним методом

Призначення відрізка прямої, направленого під кутом 45º до координатних вісей f₁ і f₂ – перетворення горизонтального напряму вісі f₁ вхідного сигналу у вертикальне. Графічні побудови, як і у попередньому випадку, вельми прості.

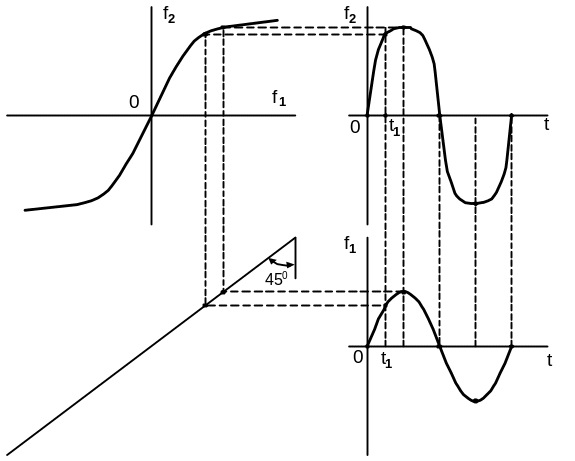
Рисунок 3.3 – До визначення реакції НРК вдосконаленим

графічним методом

Гідність графічного методу: наочність, простота, можливість знаходження характеристики, що забезпечує необхідне перетворення сигналу.

Для аналітичного визначення реакції f₂(t) необхідно мати аналітичні вирази як для вхідного сигналу f₁(t), так і вхідної або передаточної характеристики НРК. Якщо характеристика кола задана у вигляді графіку, то вона попередньо шляхом апроксимації повинна бути приведена до аналітичного виду. Хай характеристика НРК у аналітичному вигляді вже представлена наступною залежністю:

f₂(t)=g(f₁). (3.2)

Якщо вхідний сигнал змінюється за законом f₁= f₁(t), то шукану реакцію можна одержати підстановкою f₁ у залежність (3.2):

f₂(t)=g[f₁(t]).

Таким чином, аналітичне визначення дає вихідну реакцію f₂ у вигляді явної функції часу t. Головна гідність аналітичного методу визначення реакції кола – можливість робити висновки про деякі загальні властивості НРК, що мають принциповий характер. Один з таких висновків відноситься щодо перетворення спектрів сигналів нелінійним колом.

3.5 Перетворення спектра сигналу в нелінійних колах

Одна з найважливіших властивостей нелінійного кола полягає в зміні форми і перетворенні спектрального складу вхідного сигналу. Тобто при дії на вході кола гармонійного або періодичного сигналу, що складається з суми декількох гармонік різних частот, реакція НРК містить не тільки гармоніки вхідного сигналу, але також нові гармоніки, яких немає у спектрі вхідного сигнала. При цьому частоти нових гармонік можуть бути як кратними, так і не кратними основній частоті періодичної вхідної дії. Вказана властивість принципово не можлива в лінійних колах, що містять елементи із зосередженими параметрами.

3.5.1 Хай характеристика НРК задана у вигляді наступного полінома:

(3.3)

Для усунення зайвих індексів в (3.3) у якості реакції приймаємо струм i, а як вхідний сигнал – напругу u.

Спочатку розглянемо дію на вході кола гармонійного сигналу амплітудою U, частотою  і початковою фазою ₀ :

u(t)=U·cos(t +₀). (3.4)

Для отримання реакції кола „i” необхідно функцію (3.4) звести в ступені (k=1, 2, 3 …n) і виконати сумування з урахуванням коефіцієнтів B_k. З метою спрощення аналізу обмежимось ступенем поліному n =3. Для k=2 і k=3 будемо мати:

;

,

Примітка: відомо, що , звідки .

З наведеного видно, що гармонійна функція ступеня n еквівалентна сумі гармонік кратних частот, тобто тригонометричному поліному. При цьому парному значенню n відповідає сума парних гармонік, включаючи і нульову, а непарному – сума непарних гармонік. Щонайвища частота гармонік визначається ступенем полінома, тобто _max = n.

Якщо (3.4) підставити в (3.3), то після відповідних перетворень можна записати, що:

. (3.5)

Тобто, реакція НРК при дії гармонійного сигналу на вході є негармонійною періодичною функцією, що складається з суми гармонік до n-ої включно, де n – ступінь полінома, що задає характеристику кола.

3.5.2 Тепер розглінемо випадок, коли на вході кола діє сигнал, що складається з суми двох гармонік з частотами ₁ і ₂:

. (3.6)

Реакція НРК в цьому випадку складатиметься з суми ступенів двочленів:

. (3.7)

Ступені двочленів для n=2 и n=3 будуть:

n=2 - ;

n=3 - .

З наведеного вище видно, що при дії на вході кола сигналу у вигляді суми двох гармонік з частотами ₁ і ₂ реакція кола містить крім ступенів цих гармонік ще і додаткові складові, що утворюються шляхом множення різних ступенів гармонік, тобто складові вигляду і т.д. В загальному випадку ці додаткові складові в реакції кола у аналітичному вигляді можна записати , де m=1, 2, 3, …(n-1), n – ступінь полінома, що задає характеристику кола.

Відомо, що результат перемножування двох гармонійних функцій з частотами ₁ і ₂ містить теж гармонійні функції, частоти яких дорівнюють різницям або сумам двох частот ₁ і ₂. У загальному випадку частоти _mn додаткових гармонійних складових в правій частині виразу (3.7) можуть бути записані наступним чином: _mn=m₁  n₂, де m=1,2…n-1, n=1,2,3…- визначаються ступенями гармонійних функцій з частотами ₁ и ₂.

Гармонійні коливання в реакції кола з частотами _mn, що визначаються різницями або сумами частот, кратних частотам діючих на вході кола гармонік, називаються комбінаційними коливаннями. Суму абсолютних значень цілих чисел “m” і “n”, що задають кратність частот, називають порядком комбінаційних коливань.

Таким чином, результуюча реакція НРЦ на вхідний сигнал у вигляді суми двох гармонік міститиме гармонійні функції кратних частот (аж до n-ої гармоніки включно) і комбінаційні коливання до n-го порядку. У загальному випадку різницева і сумарна частоти _mn не є кратними частотам ₁ і ₂, тому вихідна реакція НРЦ не є періодичною функцією. Тільки тоді, коли частоти ₁ і ₂ кратні, вихідна реакція кола буде періодичною функцією часу.

Приклад 3.1. Визначити спектральний склад реакції НРК, характеристика якого задана поліномом другого порядку (n=2).

а) Хай на вході кола діє одна гармоніка частотою ₀ і амплітудою U. При цьому на виході кола буде:

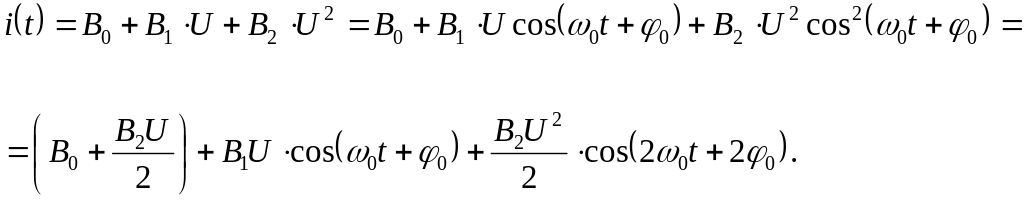
Примітка: .

З наведеного видно, що реакція НРК містить гармонійні складові з частотами 0, ₀ і 2₀; амплітуди гармонік істотно залежать від коефіцієнтів B_к характеристики. Початкові фази гармонік дорівнюють початковій фазі вхідного сигналу, помноженої на номер гармоніки. Амплітудні спектри вхідного сигналу (а) і реакції кола (б) наведено на рисунку нижче.

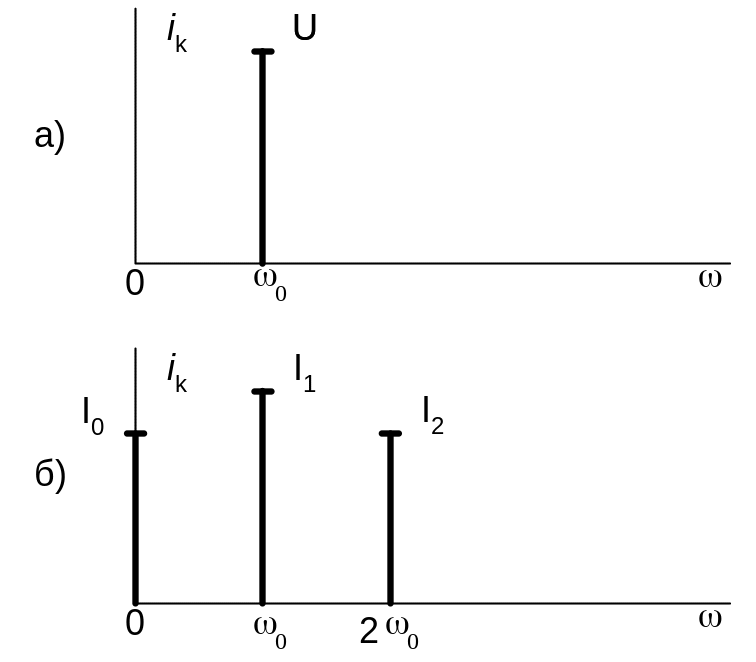
Рисунок 3.4 – Спектри амплітуд гармонійного сигналу на вході

кола (а) і реакції НРК (б) при n=2.

б) Пусть на вході кола діє сигнал, що складається з двох гармонік:

.

В цьому випадку реакція НРК буде мати наступний вигляд:

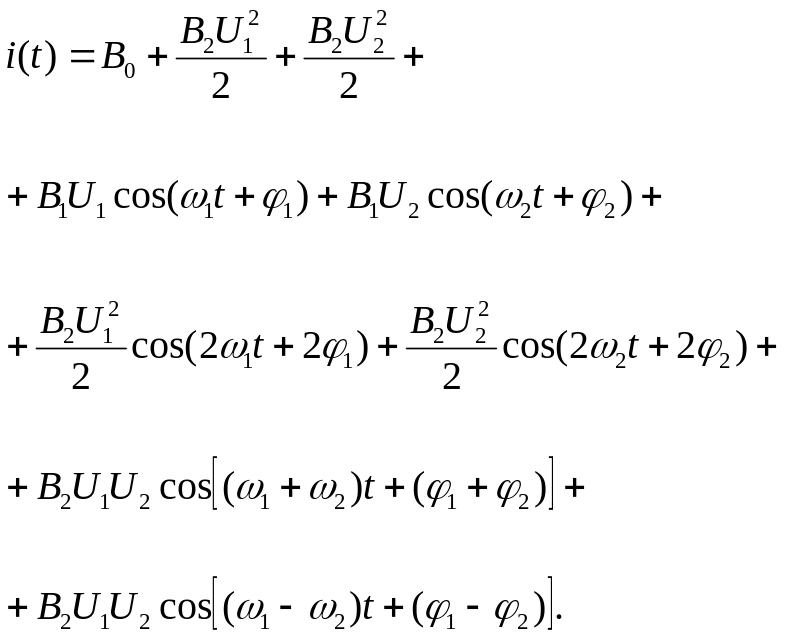
У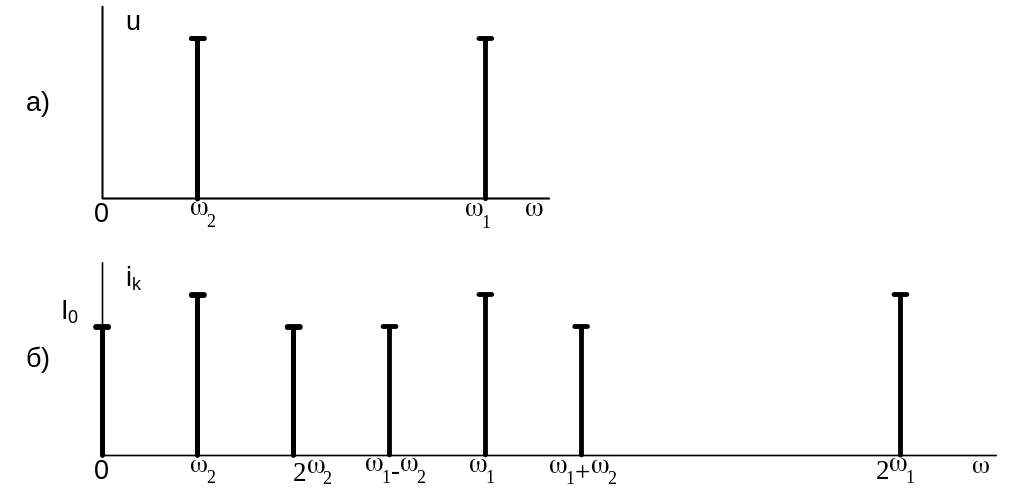 правій частині наведеного рівняння записано: а) у першій строчці – значення постійної складової сигналу на виході кола, б) у двох наступних - гармоніки з основними частотами ₁ і ₂ та кратні гармоніки з частотами 2₁ і 2₂, в) у двох останніх – комбінаційні гармоніки з частотами ₁ ₂. Амплітуди гармонік і комбінаційних коливань в значній мірі залежать від коефіцієнтів В_к характеристики НРК. Початкові фази комбінаційних коливань дорівнюють ₁₂, тобто визначаються таким же чином, як і їх частоти. Спектри амплітуд вхідного сигналу (а) кола і її реакції (б) наведено на рисунку нижче.

Рисунок 3.5 – Спектри амплітуд вхідного сигналу (а)

і реакції НРК (б) при n=2 і дії на вході кола двох гармонік

3.6 Чисельні методи розв’язання функціональних рівнянь

Розв’язання системи нелінійних функціональних рівнянь, що описує НРК, може бути виконане чисельними методами. Для цього всі коефіцієнти рівнянь повинні бути задані чисельно. В процесі рішення система рівнянь шляхом підстановок і перетворень повинна бути приведена до одного рівняння з одним невідомим або, якщо це неможливо, до мінімального числа рівнянь.

Найчастіше чисельне рішення функціональних рівнянь виконується в два етапи. Спочатку визначається груба оцінку коріння (рішення). Потім виконується уточнення значення коріння (рішення) на основі прийнятого уточнюючого алгоритму до отримання результату необхідної точності. Робиться це, як правило, за допомогою ЕОМ.

Грубу оцінку рішення можна виконати різними методами. Якщо система зведена до одного функціонального рівняння f(x)=0, то зручно скористатися графічним методом. Для цього функцію f(x) представляють у вигляді: f(x) = f₁(x) + f₂(x). Кожна з функцій f₁(x) і f₂(x) повинна мати по можливості простий графік. На практиці вказане представлення f(x) у вигляді суми 2-х функцій, як правило, не визиває особливих труднощів. Запис рівняння f(x)=0 у вигляді f₁(x)= -f₂(x) показує, що шукане рішення є точкою перетину графіків функцій f₁(x) і -f₂(x).

Уточнення рішення може побути виконано теж кількома методами. Стосовно випадку, коли система функціональних рівнянь вже зведена до одного функціонального рівняння f(x)=0, раціонально застосувати для уточнення рішення метод Ньютона – Рафсона. Суть метода полягає у наступному. Хай х=х_к є наближеним значенням рішення функціонального рівняння f(x)=0. Для отримання уточненого значення рішення х_к+1 слід ввести поправку h_k і прийняти, що х_к+1 = х_к+ h_k. Для визначення поправки h_k треба розкласти функцію f(x) у ряд Тейлора при х_к+1= х_к+ h_k . Враховуючи тільки лінійні члени розкладання в ряд, можна записати:

. (3.8)

Припускаючи, що уточнене значення х_k+1 є шукане значення, що перетворює (3.8) у нуль, знайдемо потрібну поправку:

, звідки

. (3.9)

Із (3.9) видно, що для отримання поправки h_k треба обчислити значення функції f(x) та її похідної при х=х_k.

Таким чином, алгоритм уточнення рішення функціонального рівняння за методом Ньютона-Рафсона має наступний вигляд:

(3.10)

Уточнення рішення починають з грубого наближення, вважаючи х= х₀ , (k=0). Для х₀ визначають поправку h₀ за (3.9) і уточнене значення рішення х₁ за (3.10). Потім послідовно визначають h₁ і х₂, h₂ і х_3, h₃ і х₄ і т.д. Розрахунки за наведеним алгоритмом продовжують до тих пір, доки поправка h_k не стане менше, ніж задана похибка визначення рішення (коріння).

Геометричне тлумачення методу Ньютона – Рафсона надано на рис. 3.6.

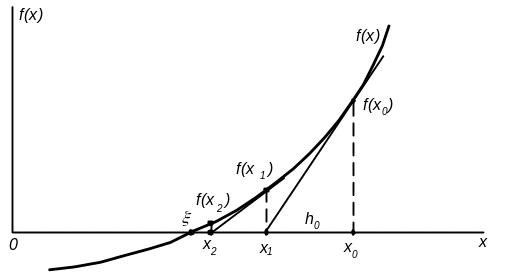
Рисунок 3.6 - Геометричне тлумачення методу Ньютона – Рафсона

Тут для ілюстрації показана функція f(x), грубе наближення рішення х₀. Це значення дає f(x₀), причому в даному випадку f(x₀)>0. Далі проводиться дотична до функції f(x) при х=х₀; дотична продовжується до перетину з віссю “х” і одержується значення поправки h₀ і нове значення коріння x₁. Повторення процесу на наступному кроці уточнення дає нове значення поправки h₁ і нове значення коріння х₂ , і т.д. Після декількох уточнень можна набути значення коріння x_к+1, достатньо близьке до точного значення коріння (його визначає т .  - точка перетину f(x) з віссю “х”).

Описаний процес уточнення рішення залежно від виду функції f(x) і вибору початкового наближення x₀ може сходитися (тобто давати шукане значення коріння) або розходиться. Якщо початкове наближення вибране достатньо близько до істинного значення коріння, то чисельний процес завжди сходиться і можна одержати рішення з будь-якою точністю. При цьому метод Ньютона – Рафсона забезпечує вищу збіжність, ніж інші методи уточнення. У разі розбіжності чисельного процесу слід задатися новим наближеним значенням рішення х₀ і повторити процес уточнення.

Наданий алгоритм процедури послідовного уточнення рішення функціонального рівняння за методом Ньютона – Рафсона для зменшення часових витрат раціонально реалізувати із застосуванням ЕОМ.

Метод ітерацій. Існує простіший, але менш ефективний метод уточнення рішення функціонального рівняння - метод ітерацій. Суть методу зводиться до наступного. Функціональне рівняння f(x)=0 приводиться до вигляду: x=g(x). Потім в праву частину цього рівняння підставляють наближене значення x₀. Одержану величину g(x₀) приймають за уточнене значення х₁=g(x₀), яке знову підставляють в g(x). Повторення цього процесу, як процедуру уточнення рішення рівняння f(x)=0, можна записати у вигляді наступного алгоритму:

x_к+1=g(x_к), к=0, 1 ,2, 3 ….

Він дозволяє набути значення коріння з будь-якою малою похибкою, якщо процес ітераційного уточнення рішення сходиться. Умова збіжності ітерацій записується таким чином:

,

тобто на інтервалі між точним і наближеним значенням коріння кут нахилу дотичної не повинен перевищувати 45º. Якщо вказана умова не виконується, слід переробити початкове рівняння x=g(x).

Геометричне тлумачення методу простих ітерацій наведено на рис. 3.7.

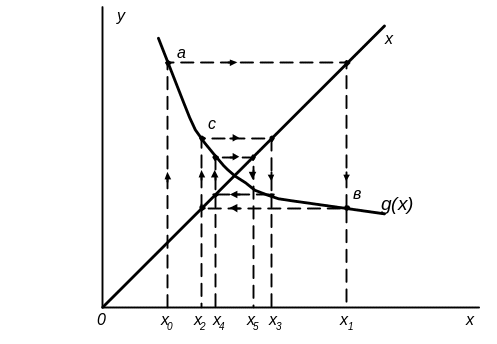
Рисунок 3.7 - Геометричне тлумачення методу ітерацій

Тут показано графіки двох функцій: а) y= g(x), б) y=x (пряма, що проходить через початок координат під кутом 45º). Точка їх перетину дає точне значення рішення рівняння.

Наближене значення x₀ визначає т. а, ордината якої приймаються за уточнене значення рішення х₁. Для його знаходження проводиться горизонтальна лінія до перетину з прямою y=x, а звідти – вертикальна лінія до перетину з кривою y=g(x) –отримана т. в, абсциса якої дорівнює х₁, а ордината – g(x₁). Остання приймається за нове (уточнене) значення рішення. Далі таким же чином визначається т. с і т.д. Як видно, процес ітерації сходиться при |g(x₀)|<1 , а при невиконанні умови процес буде таким, що не сходиться.

Розглянутий вище процес попереднього визначення грубого рішення функціонального рівняння і подальшого його уточнення дозволяє отримати лише одне значення реакції НРК (воно відповідає одній точці характеристики кола) для заданого значення вхідного сигналу, який вважається постійним. Для знаходження решти значень реакції необхідно задаватися іншими значеннями вхідного сигналу і вирішувати нові функціональні рівняння. Зрозуміло, що для складних кіл потрібен великий об'єм обчислень, який можна здійснити лише за допомогою ЕОМ.

Застосування чисельних методів в аналізі НРК передбачає необхідність складання функціональних рівнянь, що описують схему, і апроксимації в.а.х. нелінійних елементів аналітичними виразами. Апроксимація завжди вносить похибку. Причому, чим простіше вид апроксимуючого виразу, тим більше похибка. Необхідність апроксимації в.а.х. елементів схеми – основний недолік чисельних (також і аналітичних) методів. Другий недолік полягає у тому, що в результаті розрахунків не можна одержати якісні уявлення про вплив окремих елементів і їх характеристик на властивості схеми в цілому, що дуже істотне при проектуванні. Крім того, чисельний метод не дає всіх можливих рішень у тому випадку, коли не існує єдиного рішення.

Гідність чисельних методів –можливість застосування до рішення функціональних рівнянь кіл будь-якої конфігурації, якщо задовольняються умови існування єдиного рішення.

Приклад 3.2. Коло, що складається з 2-х послідовно з’єднаних нелінійних елементів, підключено до джерела постійної напруги U=1В. В.а.х. нелінійних елементів відомі і мають наступний вид:

Визначити струм в колі і напругу на кожному нелінійному елементі, користуючись методом Ньютона – Рафсона.

Розв’язання.

• Для даного кола відповідно до другого закона Кирхгофа можна записати наступне рівняння (i₁ = i₂ = i):

 .

• Складаємо функціональне рівняння: .

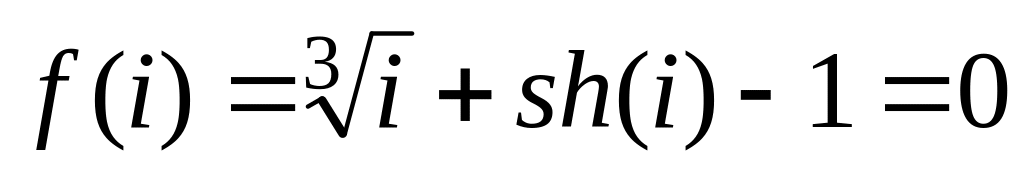• Визначаємо похідну

.

• Будуємо графіки функцій 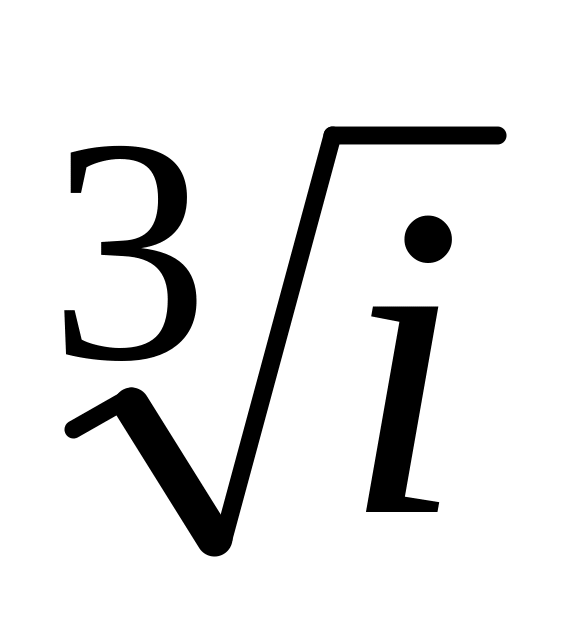і sh(i) і в точці перетину графіків приймаємо початкове (грубе) значення рішення i₀=0,3.

• Знаходимо: f(i₀)=f(0,3)=0,3^1/3+sh(0,3)-1 = -0,0262 ;

.

• Обчислюємо першу поправку 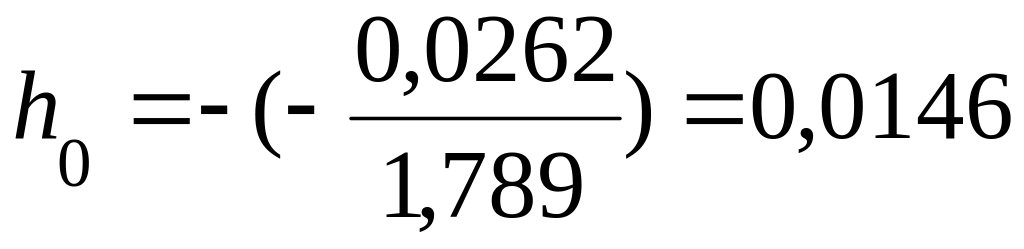і перше уточнення рішення i₁ = i₀+h₀ = 0,3+0,0146 0,315.

• Визначаємо f(i₁)=f(0,315)=0,315^1/3+sh(0,315)-10. Отже h₁ 0 и вже перший крок дає точне значення коріння: i₁ = i₀+h₀ =0,315.

• Підстановкою i=0,315 в аналітичні вирази в.а.х. нелінійних елементів, знайдемо падіння напруги на них.

3.7 Метод перетворення схем

При аналізі широкого класу нелінійних кіл часто застосовується метод перетворення схем. Він не має такої спільністі, як чисельний метод, але вельми корисний при аналізі паралельно – послідовних кіл з одним джерелом змінного сигналу. Суть методу перетворення зводиться до послідовної заміни паралельно (послідовно) з’єднаних елементів однією еквівалентною гілкою, тобто послідовного знаходження еквівалентної в.а.х. двох з’єднаних паралельно (послідовно) резистивних елементів. Метод дозволяє виконувати розрахунки без складання рівнянь за допомогою графічних побудов. При цьому мають справу безпосередньо з в.а.х., які звичайно задаються у вигляді графіків. Вигляд в.а.х. і ступінь її складності не впливають на хід розрахунків. За допомогою графічних побудов можна одержати відразу всі можливі рішення (якщо їх декілька).

При послідовному з'єднанні елементів справа зводиться до графічногорішення наступних рівнянь:

При паралельному з'єднанні вирішується наступна система:

Процес послідовного знаходження еквівалентної в.а.х. паралельно (послідовно) з’єднаних елементів кола, як правило, починається з вихода схеми і закінчується отриманням вхідної характеристики кола щодо джерела сигналу. Аналогічним чином може бути отримана і передаточна характеристика схеми.

Рішення систем рівнянь, приведених вище, можуть бути виконані і аналітично. Для цього треба мати в.а.х. елементів, представлені в аналітичному вигляді. Проте слід звернути увагу на те, що при переходах від паралельного з'єднання до послідовного і від послідовного до паралельного часто виникає потріба обернення в.а.х. елементів, що в аналітичному вигляді не завжди можливо здійснити.

3.8 Аналіз нелінійних кіл методом послідовних кусково-лінійних схем

Метод послідовних кусково-лінійних схем базується на заміні в.а.х. всіх нелінійних елементів кола кусково-лінійними наближеннями. Це істотно спрощує аналіз нелінійного кола, оскільки в інтервалах між зламами характеристик коло (схема) виявляється лінійним, тобто аналіз може бути проведений простими методами теорії лінійних кіл.

Гідності методу: а) дозволяє виконати аналіз кола будь-якої конфігурації, що містить як двохполюсні, так і багатополюсні елементи, в т.р. і керовані джерела; б) в межах лінійних ділянок апроксимуючої характеристики (тобто за винятком окремих точок зламу в.а.х.) мають справу з лінійною схемою, для аналізу якої можна застосувати методи теорії лінійних кіл.

Кусково-лінійну схему заміщення отримують шляхом представлення кожного нелінійного елементу на лінійній ділянці його апроксимуючої в.а.х. лінеарізованной схемою, яка складається з лінійного резистивного елементу і джерела постійної напруги або струму.

3.9 Кусково-лінійні схеми заміщення нелінійних елементів

електронних кіл

Схеми заміщення найчастіше складають на основі кусково-лінійного представлення в.а.х. нелінійних елементів. Це неминуче приводить до того, що характеристики схеми заміщення (або моделі) відрізняються від характеристик елемента. Точність наближення можна підвищити за рахунок збільшення кількості інтервалів лінійного наближення, але при цьому істотно зростає складність (об’єм) розрахунків з використанням такої моделі. Як завжди, при складанні схеми заміщення необхідний компромісний вибір між точністю моделі і складністю розрахунків.

Реальний діод. На відміну від ідеального діода у реального діода: а) падіння напруги в прямому напрямі не рівно нулю; б) струм у зворотному напрямі також не рівний нулю. Кількісні характеристики прямої і зворотної гілок в.а.х. різних діодів істотно відрізняються, але цю відмінність можна врахувати значеннями параметрів схеми заміщення без зміни її вигляду.

У першому наближенні в.а.х. реального діода може бути представлена двома лінійними ділянками з точкою зламу на початку координат (рис. 3.8а). Вказаній кусково-лінійній характеристиці відповідає схема заміщення, що наведена на рис. 3.8б.

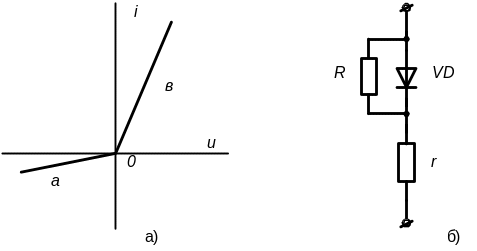
Рисунок 3.8 - Кусково-лінійна апроксимація в.а.х.

реального діода (а) і схема заміщеня діода (б)

У цій схемі послідовно з ідеальним діодом VD включений опір r, що враховує падіння напруги в прямому напрямі і який вибирається виходячи з необхідного нахилу ділянки “в” характеристики. Зворотний струм діода враховує опір R>>r, включений паралельно ідеальному діоду VD.

При необхідності кусково-лінійне наближення може містити більшу кількість відрізків, що відповідно підвищить складність схеми заміщення.

Керований двополюсний елемент. Для отримання схем заміщення керованих елементів необхідно використовувати залежні джерела, керовані відповідними сигналами, параметри яких визначаються за в.а.х. елементу.

Розглянемо керований двополюсний елемент, в.а.х. якого під дією зовнішнього параметра, що керує, зміщуються у напрямі вісі напруг. Такі характеристики має, наприклад, термістор (рис. 3.9), опір і в.а.х. якого залежать від температури Т.

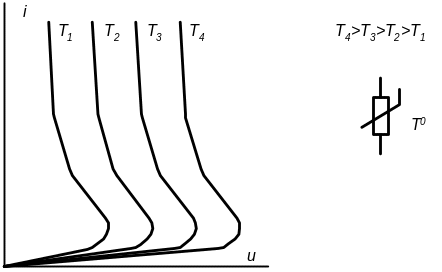
Рисунок 3.9 – Сімейство в.а.х. термістора

Такий елемент можна моделювати схемою заміщення, що наведена на рис. 3.10.

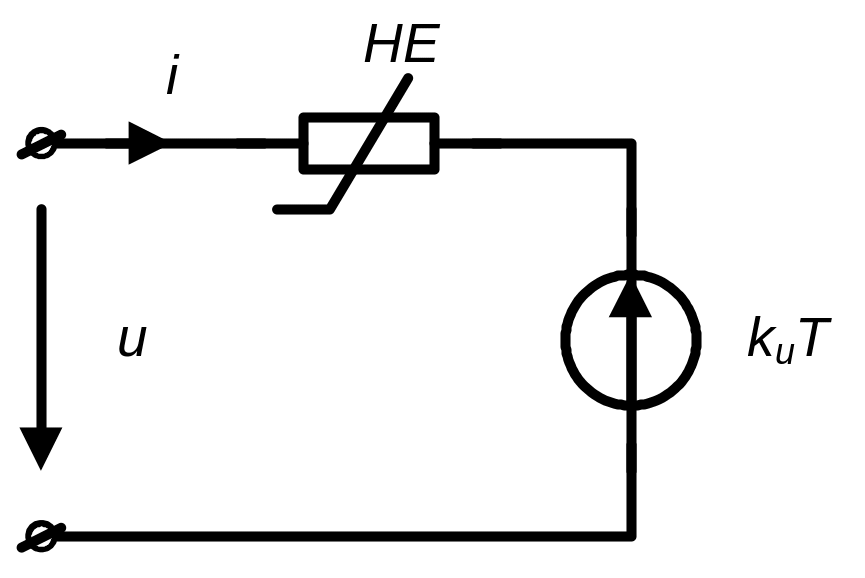
Рисунок 3.10 – Схема заміщення термістора

Схема містить: а) нелінійний резистивний елемент НЕ, характеристика якого відповідає в.а.х. термістора при Т=0, б) послідовно включене кероване (залежне) джерело напруги k_uT, е.р.с. якого пропорційна параметру, що керує, – температурі Т. Результуюча в.а.х. формується шляхом сумувування напруги джерела k_uT з абсцисами нелінійної в.а.х.елемента НЕ. Результуюча характеристика схеми при заданому значенні температури Т_і, тобто е.р.с. джерела k_uТ_і , отримується зсувом характеристики резистивного двополюсника НЕ управо вздовж вісі напруги при зростанні Т і вліво - при зменшені Т.

При необхідності сформувати більш докладну схему заміщення термістора (ніж та, що наведена на рис. 3.10), потрібно в.а.х. термістора при Т=0 (тобто в.а.х. резистивного елемента НЕ) апроксимувати кусково – лінійною характеристикою, відповідно до неї скласти кусково-лінійну наближену схема заміщення (як це зроблено для реального діода) і замінити на рис. 3.10 елемент НЕ його кусково-лінійною схемою заміщення.

У разі керованого двополюсного елемента типа фотодіода, характеристика якого під дією параметра Ф, що керує, зсовується уздовж вісі струму i (див. рис. 3.11а), одержимо схему заміщення, що містить кероване (залежне) джерело струму к_iФ (рис. 3.11б).

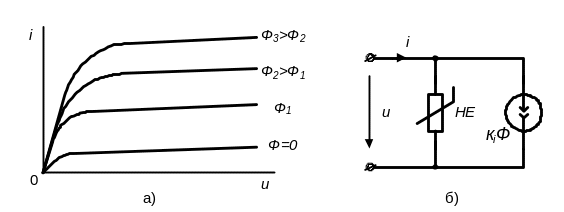
Рисунок 3.11 – В.а.х. фотодіода (а) і їх електрична модель (б)

Схема складається з паралельного з'єднання нелінійного резистивного елементу НЕ, характеристика якого відповідає Ф=0, і джерела, струм якого пропорційний значенню параметра Ф, що керує (світлового потоку). Струми обох елементів складаються, тому при зміні параметра Ф характеристика резистивного елементу зміщуватиметься уздовж осі струму.

Вакуумний тріод. При складанні схеми заміщення тріода для режиму великих сигналів будемо вважати, що: а) анодна напруга u₂ не впливає на сітковий струм i₁; б) сітковий струм i₁ не досягає області насичення. В цьому випадку вхідну (сіткову) і вихідні (анодні) в.а.х. вакуумного тріода можна представити кусково-лінійними наближеннями, зображеними на рис. 3.12. Тут: u₁ – сіткова напруга, i₁ - сітковий струм, u₂ – анодна напруга, i₂ – анодний струм тріода.

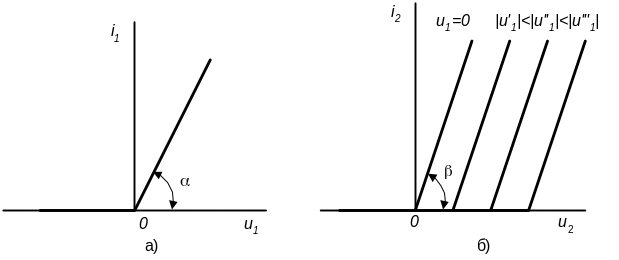
Рисунок 3.12 - Кусково-лінійні наближення вхідних (а)

і вихідних (б) в.а.х. вакуумного тріода

Вхідна характеристика зображена у вигляді кусково-лінійної кривої (рис. 3.12а), що складається з двох ділянок:а) горизонтальної, яка співпадає з віссю “u₁” (u₁<0), б) лінійно зростаючої, що утворює кут  з віссю “u” при u₁>0 (tg =1/r_д, де r_д - опір кола сітки тріода). Цій характеристиці відповідає схема вхідного контура (рис. 3.13), що складається з послідовно з’єднаних ідеального діода VD1 і резистора r_д.

Анодні характеристики при різних значеннях напруги на сітці u₁ подано на рис. 3.12б кусково-лінійними кривими, які зміщуються одна відносно одної залежно від значення сіткової напруги u₁. Кожна крива складається з горизонтальної ділянки, що збігається з віссю u₂=u_a, і лінійно зростаючої ділянки з кутовим коефіцієнтом tg=1/r_i, де r_i – внутрішній опір тріода (r_i=u_a/i_a , i_a = i₂ ). Першому наклонному відрізку вихідних кусково – лінійних характеристик при u₁ = u_с = 0 відповідає схема з послідовно з’єднаними ідеальним діодом VD2 і резистором r_і (рис. 3.13). Зі зміною сіткової напруги u₁ характеристики зміщуються за допомогою джерела напруги, е.р.с. μu₁ якого керується вхідною (сітковою) напругою u₁ .

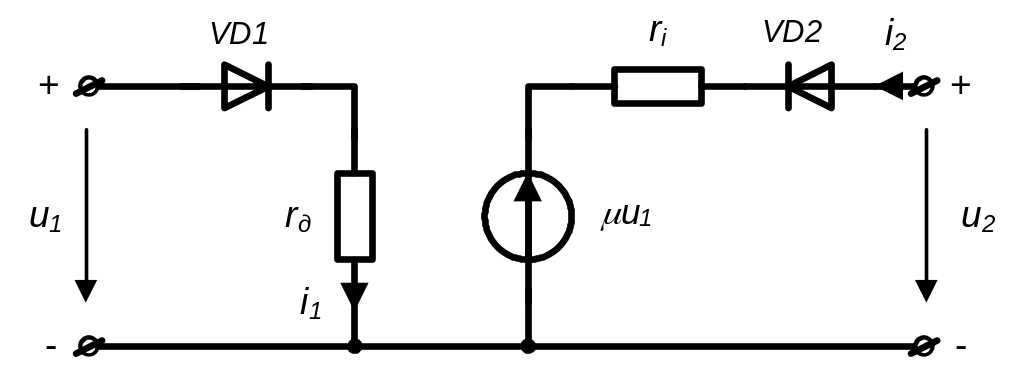
Рисунок 3.13 – Схема заміщення вакуумного тріода

Пентод. Найчастіше в пентоді управління здійснюється тільки по 1-й (управляючій) сітці. Тому його можна розглядати як трьохполюсний керований резистивний елемент. Вхідні в.а.х. пентода не відрізняються від в.а.х. тріода, тому і схема заміщення сіткового кола буде такою ж як і у тріода.

На рис. 3.14 надано кусково-лінійне наближення сімейства анодних характеристик пентода при різних значеннях напруги на управляючій сітці.

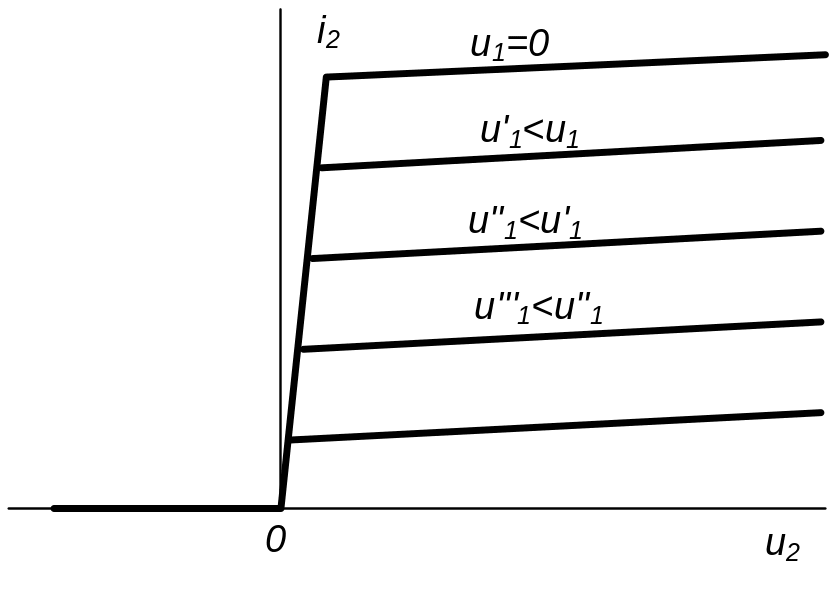
Рисунок 3.14 - Кусково-лінійне наближення анодних в.а.х. пентода

Кожна апроксимуюча кусково – лінійна в.а.х. має три ділянки: а) ділянку, що співпадає з віссю абсцис при u₂<0; б) лінійно зростаючу ділянку (середню) з однаковим нахилом для всього сімейства в.а.х.; в) майже горизонтальні відрізки прямих, що зміщуються у напрямку вісі анодного струму i₂ (приріст струму i₂ зміщуємих відрізків пропорцієн значенню напруги u₁ на управляючій сітці). Схему заміщення пентода наведено на рис. 3.15.

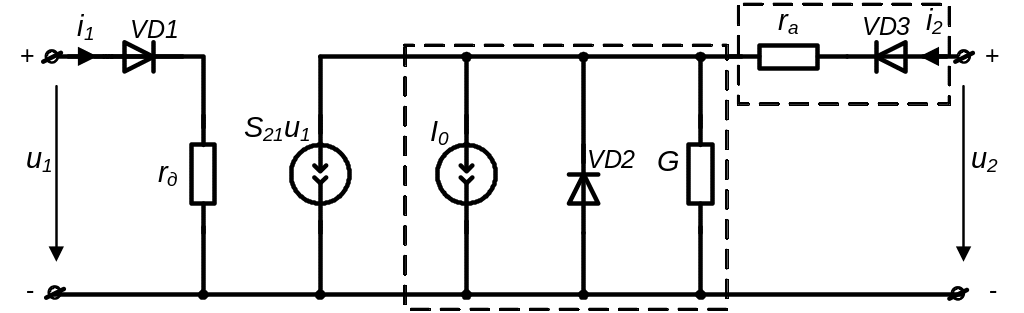
Рисунок 3.15 – Схема заміщення пентода

Сама верхня характеристика сімейства, що відповідає u₁=0, одержується за допомогою послідовного з'єднання двох блоків: а) блоку, що складається з послідовно включених ідеального діода VD3 і опору r_a – він визначає нахил зростаючої середньої ділянки в.а.х.; б) блоку, що складається з паралельно сполучених джерела струму I₀, ідеального діода VD2 і провідності G, що визначає нахил відрізків третього ділянок в.а.х. . Зміщення відрізків третьої ділянки характеристик у напрямку вісі анодного струму i₂ забезпечується включенням джерела струму S₂₁u₁, керованого вхідною (сітковою) напругою, паралельно другому блоку.

Біполярний транзистор. Розглянемо схему заміщення біполярного транзистора (БПТ) структури n – p – n, включеного за схемою СЕ (спільний емітер). Таке включення часто застосовується в різних перемикаючих пристроях у режимі великого сигналу. Кусково-лінійне наближення вихідних характеристик біполярного транзистора надано на рис. 3.16.

Рисунок 3.16 - Кусково-лінійне наближення вихідних в.а.х. БПТ

Нахили відрізків третьої ділянки характеристик при u₂>0 прийняті приблизно однаковими; відстані між відрізками пропорційні вхідному (базовому) струму i_б= i₁. При цьому відношення колекторного струму до струму бази дорівнює коефіцієнту підсилення вихідного струму β=i_k/i_б=i₂/i₁. Нижня з характеристик відповідає нульовому значенню вхідного струму i₁=i_б=0; її можна отримати за допомогою елементарного блоку з опуклою характеристикою, який складається з паралельно з'єднаних джерела струму J₀, ідеального діода VD2 і резистивного елементу, опір якого 1/G залежить від нахилу відрізків третьої ділянки характеристик (рис. 3.16). Всі інші відрізки вихідних в.а.х. можна отримати за допомогою керованого вхідним струмом i₁ джерела струму βi₁ . Кероване джерело приєднується до вказаного вище блоку паралельно (див. рис. 3.17). Опор r_a визначає нахил зростаючої середньої ділянки в.а.х.

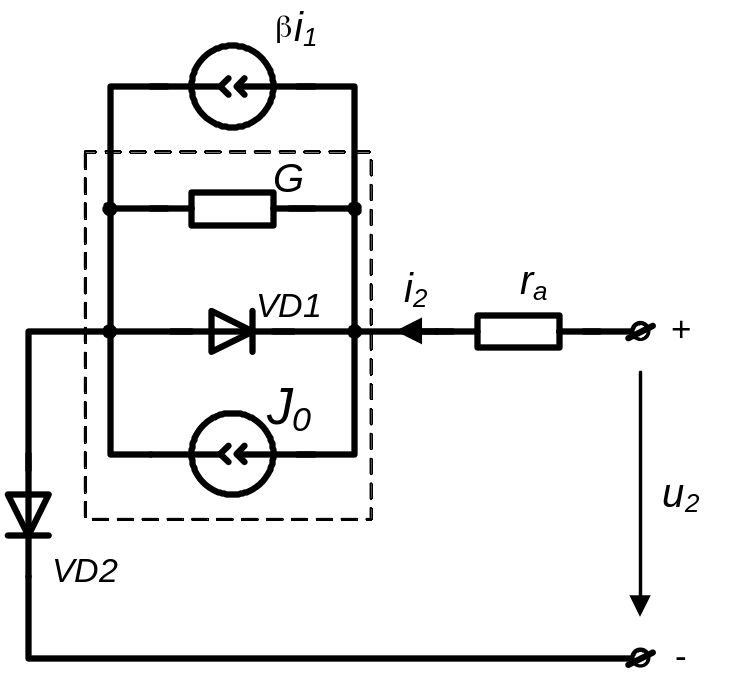
Рисунок 3.17 – Електрична модель вихідних в.а.х. БПТ

Для вхідних характеристик транзистора можна прийняти кусково-лінійне наближення, що надано на рис. 3.18.

Рисунок 3.18 – Кусково-лінійне наближення

вхідних характеристик транзистора

Характеристику, що відповідає нульовому значенню напруги u₂=0, можна одержати за допомогою елементарного блоку, який містить послідовно з'єднані джерело напруги u₀₁, ідеальний діод VD і опір r₁ (див. рис. 3.19).

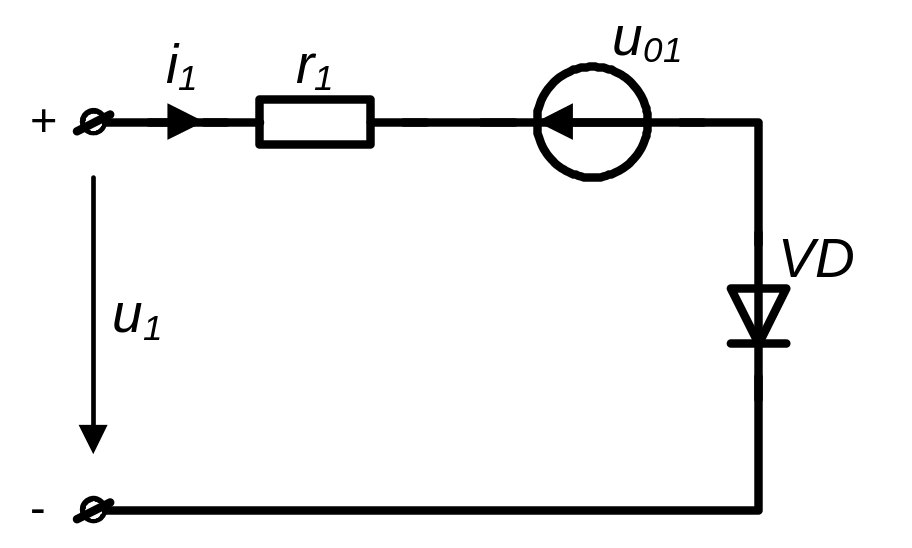
Рисунок 3.19 – Електрична модель вхідної

в.а.х. транзистора при u₂=0.

Решта характеристик (u₂>0) може бути отримана при необхідності послідовним приєднанням до вказаного блоку джерела напруги, керованого вихідною напругою u₂ .

З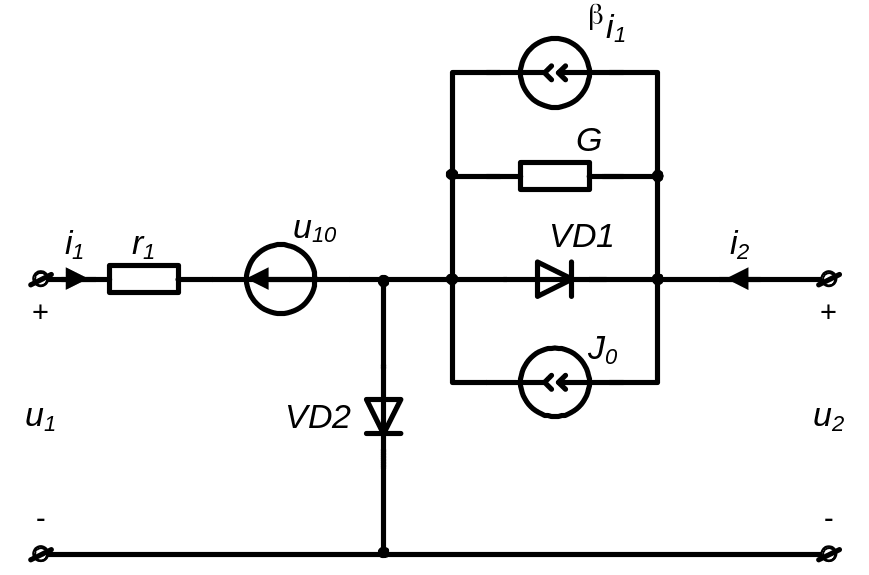 урахуванням наведеного вище отримана наступна схема заміщення транзистора (рис. 3.20). Для спрощення схеми на рис. 3.20 не показані блоки, що моделюють сімейство вхідних характеристик при u₂>0, і нахил вихідних в.а.х. на середній зростаючій ділянці.

Рисунок 3.20 – Спрощена схема заміщення

біполярного транзистора