3 Статичний аналіз
3.1 Общая характеристика нелинейных цепей
В теории линейных цепей считается, что параметры всех элементов - резисторов, емкостей, индуктивностей - имеют постоянные значения, зависят от токов и напряжений на их выводах, а так же от времени. Каждому из этих элементов можно приписать определенное значение параметра - сопротивление R резистору, емкость С конденсатора, индуктивность L катушке индуктивности, соответственно. Предположение постоянства значений параметров является идеализацией. На самом деле параметры элементов некоторой степени зависят от тока i или напряжения u, а также времени t. Поэтому постоянство параметров возможно принимать лишь в ограниченных пределах изменений i и u.
Круг считается линейным, если оно удовлетворяет следующим условиям:
1) [f(х1+х2) = f(х1)+f(х2)],
2) f(а∙х)=а∙f(х).
Перше рівняння відображає властивість адитивності кола, друге – його однорідність (в наведених виразах вхідна дія кола позначена як „х”, а реакція кола на вхідну дію – як „f”). При аналізі лінійних кіл широко застосовують принцип суперпозиції саме тому, що вони задовольняють цим умовам - адитивності та однорідності.
Існує значний клас елементів і пристроїв, параметри яких істотно залежать від i і u. Такі елементи називаю нелінійними. Їм не можна приписати якісь певні значення параметра при варіації змінних кола (i або u) в якомусь діапазоні. Для кількісної характеристики таких нелінійних елементів і опису їх властивостей необхідно задавати залежності струму i від напруги u, тобто в.а.х.. Найчастіше їх визначають експериментально і представляють у графічному вигляді.
З погляду аналізу одна з головних особливостей нелінійних кіл полягає у тому, що до них неможна застосовувати принцип суперпозиції, бо вони не мають властивостей адитивності та однорідності. Розглянемо, наприклад, нелінійний елемент, з нелінійною в.а.х. виду i = а u2 , де напруга „u” розглядається як входна дія, а струм „i” - як реакція. Якщо прикладену до елементу напругу u представити у вигляді суми двох складових u1 і u2 (тобто u =u1+u2), то струм в такому нелінійному елементі можна записати у вигляді
i = а(u1 + u2)2 = а(u12 + 2u1u2 +u22).
Якщо ж визначити сумарний струм від дії кожної з складових напруги порізно, то одержуємо:
i = i1 + i2 = а(u12 + u22),
тобто набуваємо інше значення струму. Таким чином, умова адитивності не виконується і принцип суперпозиції не може бути застосований.
Для лінійних кіл принцип суперпозиції може застосовуватись і широко використовується. Достатньо знати реакцію кола на дію сигналу однієї форми (наприклад, одиничний стрибок, одиничний імпульс або гармонічна функція), щоб знайти реакцію кола на дію сигналу довільної форми за допомогою інтеграла накладення або частотного методу.
Значно складніша справа з аналізом процесів в нелінійних колах, де принцип суперпозиції не застосовується. Процеси, що відбуваються в нелінійних колах, описують нелінійні алгебраїчні або диференціальні рівняння, теорія розвязання яких складна і розроблена значно гірше, ніж лінійних. Зараз не існує навіть загального підходу до рішення таких рівнянь. Існуючі методи не володіють достатньою спільністю і найчастіше можуть бути застосовані до рішення рівнянь лише певного типу. Як наслідок, не існує скільки-небудь загальних методів або прийомів аналітичного рішення нелінійних рівнянь, що описують нелінійні кола. Багато нелінійних рівнянь зараз взагалі не мають аналітичних рішень, або вимагають застосування спеціальних функцій, непридатних в інженерній практиці.
При аналізі нелінійних кіл найчастіше можна говорити лише про наближені методи рішення, що придатні для певного класу рівнянь, або про чисельні методи рішення. Особливо справа ускладнюється коли нелінійна в.а.х. задана графічно і відсутній достатньо простий математичний опис цієї нелінійності. Загалом, аналіз нелінійних кіл в загальному випадку є складною задачею, що пояснюється: а) складністю процесів, що відбуваються в них; б) відсутністю загальних способів виявлення їх особливостей і необхідністю застосування ряду методів аналізу при їх всесторонньому дослідженні.
У нелінійних колах можуть мати місце явища, принципово неможливі в лінійних. Ось деякі з них.
1. При дії на вході кола гармонійного сигналу форма реакції виявляється спотвореною, тобто вихідний сигнал містить гармоніки, яких немає у вхідному.
2. За деяких умов в нелінійному колі можуть встановитися субгармонійні коливання – коливання, частота яких в ціле число раз нижча за частоту прикладеного до кола гармонійного сигналу.
3. При дії на вході кола сигналу у вигляді суми двох і більше гармонік, вихідна реакція разом з гармоніками вказаних частот (наприклад 1 і 2) і кратних частот (к1 і n2) може містити коливання комбінаційних частот (m1 f2). У загальному випадку комбінаційні частоти відрізняються від частот складових вхідного сигналу.
4. В нелінійних колах амплітуда вихідної реакції непропорційна амплітуді вхідного сигналу; у пристроях, що використовуються як стабілізатори, в деякому діапазоні зміни вхідного u (або i) вихідне u (або i) залишається майже незмінним.
5. За відсутності зовнішніх дій з часом в колі встановлюється певний режим – стан рівноваги. Досить часто в нелінійних колах може існувати декілька станів рівноваги.
6. Існує клас нелінійних кіл, в яких можуть виникати автоколивання за відсутності зовнішньої періодичної дії. В них енергія джерел постійного струму перетвориться в енергію автоколивального процесу.
7. При плавній зміні амплітуди вхідного сигналу або частоти періодичного сигналу в нелінійних колах можуть мати місце стрибкоподібні зміни u (або i) або частоти (або фази) періодичного сигналу.
3.2 Характеристика типових нелінійних елементів резистивних кіл
Нелінійні кола, складені з елементів одного виду, наприклад, резистивних, є простішими, ніж нелінійні кола, складені з елементів різних видів. Нелінійні резистивні кола, зважаючи на відсутність в них елементів, що накопичують енергію, описуються системою алгебраічних або трансцендентних рівнянь. Рішення цих рівнянь набагато простіше, ніж рішення диференціальних рівнянь, які описують кола з трьома видами елементів.
Властивості ідеального резистивного елементу повністю визначає його в.а.х., що є залежністю струму i в елементі від напруги u на його виводах:
i = i(u).
Найчастіше в.а.х. визначають експериментально і зображають у вигляді графіка на площині “u - i”. Прийнято відкладати напругу u по осі абсцис, а струм i – по осі ординат. В.а.х. прийнято знімати шляхом зміни прикладених до елементу постійної напруги і струму, або шляхом застосування змінної напруги і струму низької частоти. Одержана таким чином в.а.х. називається статичною. Для кожного елементу або приладу існує своя гранична частота, при перевищенні якої статичними характеристиками не можна користуватися без відповідної корекції. Врахувати вплив частоти на в.а.х. елементу дуже важко. Тому користуватися статичними характеристиками можна до тих пір, поки частоти сигналів в елементі не перевищують межу, що припускається.
3.2.1 Класифікація видів в.а.х. нелінійних резистивних двополюсників.
Прийнята наступна класифікація видів в.а.х. резистивних двополюсників (дотримуючись вказаних на рис. 3.1 позитивних напрямів струмів і напруг).
а) Якщо в.а.х. нелінійного елементу розташовується тільки в I і III квадрантах (криві 1 на рис. 3.1а і б), то вона відноситься до пасивного елементу: потужність p =u·i 0, оскільки знаки “u” і “i” співпадають; в.а.х. пасивного елементу проходить через початок системи координат.
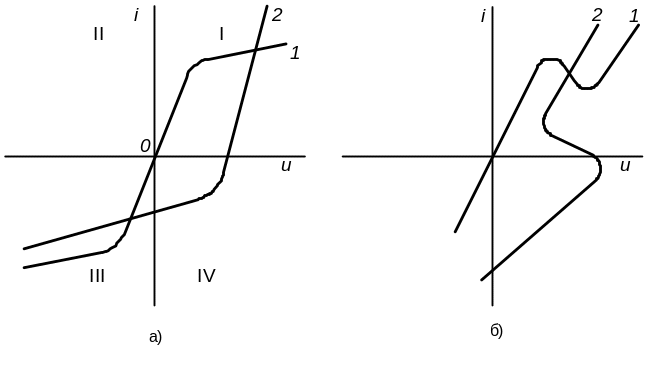
Рисунок 3.1 – До класифікації видів в.а.х. нелінійних
резистивних двополюсників
Якщо деякі ділянки в.а.х. потрапляють в II або IV квадранти, то характеристика відноситься до активного елементу: у вказаних квадрантах знаки “u” і “i” протилежні, p =u·i < 0, що означає генерацію потужності.
б) В.а.х. пасивного елементу може бути симетричною щодо початку системи координат (крива 1 на рис. 3.1а) і несиметричною (крива 1 на рис. 3.1б). Елемент з симетричною характеристикою називають двостороннім; він володіє властивістю інваріантності характеристики при зміні виводів.
в) Розрізняють монотонну і немонотонну характеристики. У разі монотонної характеристики при -<u< нахил в.а.х., тобто похідна di/du, не міняє свого знаку і залишається або позитивною (рис. 3.1а), або негативною. Якщо похідна не приймає нульового значення, тобто в.а.х. не має горизонтальних ділянок, то говорять про строго монотонну характеристику.
Якщо при -<u< нахил кривої, тобто похідна, міняє свій знак, то виходить немонотонна характеристика, тобто характеристика з падаючою ділянкою. На таких ділянках елемент має негативний динамічний опір. В більшості випадків елемент з немонотонною характеристикою має одну ділянку з негативним нахилом. Розрізняють два види характеристик подібного типу: характеристику типа N і характеристику типа S.
г) Характеристика типа N (крива 1 на рис. 3.1б) має ділянку негативного динамічного опору. Залежність між u і i така, що кожному значенню u відповідає єдине значення i – струм є однозначною функцією напруги. Характеристику типа N називають характеристикою, керованою напругою. У залежності ж від i характеристика типа N неоднозначна – деякому значенню i може відповідати три значення u. Характеристику типа N (вольт-амперну N-характеристику) мають тунельні діоди.
Характеристика типа S (крива 2 на рис. 3.1б) теж має ділянку з негативним нахилом. Але тут кожному значенню i відповідає одне значення u – напруга є однозначною функцією струму. Характеристику типа S називають характеристикою, керованою струмом. У залежності ж від u дана характеристика неоднозначна – заданій величині u можуть відповідати три значення i. Вольт-амперну S -характеристику мають диністори (некеровані тиристори).
д) На практиці часто доводиться користуватися, так званими, обернутими характеристиками. Хай задана характеристика вигляду i = i(u); обернення характеристики означає представлення її у вигляді u = u(i), тобто рішення початкового співвідношення i = i(u) щодо напруги u.
3.2.2 Загальна класифікація нелінійних резистивних елементів.
В електронній техніці застосовується велика кількість різних нелінійних елементів, тобто елементів, що мають нелінійні в.а.х.. Прийнята наступна класифікація існуючих нелінійних резистивних елементів: