4. Нелинейное квантование

В некоторых случаях линейное квантование аналогового сигнала оказывается недостаточно эффективным. Типичным примером такой ситуации является аналого-цифровое преобразование звуковых сигналов. Если звуковой сигнал, который требуется преобразовать в цифровую форму, имеет достаточно широкий динамический диапазон (например, звучание симфонического оркестра), то отношение сигнал/шум, определяемое формулой (1.13) оказывается приемлемым только для фрагментов звучания, близким к предельным значениям шкалы квантования. Когда уровень полезного (музыкального) сигнала достаточно высок, он маскирует шумы квантования и присутствие последних практически не ощущается на слух. Но для фрагментов тихого звучания музыкальной программы, когда диапазон изменения аналогового сигнала находится в пределах всего нескольких нижних уровней квантования (вплоть до m = 1), отношение сигнал/шум резко ухудшается, и воздействие шума квантования на звучание фонограммы оказывается катастрофическим. Процесс квантования в этом случае будет эквивалентен процессу жесткого ограничения, и сигнал будет иметь вид прямоугольных импульсов. Разница между входным сигналом (синусоидальная волна) и выходным сигналом (прямоугольные импульсы) выразится в появлении целого ряда нечетных гармоник с уровнем, сопоставимым с уровнем исходного аналогового сигнала. Одно из основных условий, при котором шум квантования считается эквивалентным белому шуму (высокий уровень входного сигнала) в данном случае оказывается нарушенным и ошибка квантования приобретает характер искажения. Причем, искажения эти крайне неприятны на слух.

Наиболее очевидным способом борьбы с шумом квантования представляется снижение его уровня до приемлемой величины путем повышения разрядности квантования. Согласно той же формуле (1.13) каждый добавленный разряд сокращает уровень шума на 6 дБ. В большинстве случаев именно по этому пути идут разработчики цифровой звуковой аппаратуры. Длина кодов, используемых в высококачественных системах цифровой звукозаписи, в настоящее время достигает 20-24 разрядов. Подобное решение оказывается очень эффективным, но, к сожалению, достаточно дорогим. АЦП и ЦАП с такой разрядностью изготовить весьма непросто и это, безусловно, отражается на их цене.

Альтернативным решением для систем менее высокой разрядности квантования является введение небольшого количества специально сформированного белого шума к входному аналоговому сигналу. Такой искусственно созданный белый шум называется дифером. Идея введения аддитивного шума в квантуемый сигнал принадлежит Л. Робертсу, который использовал этот прием при кодировании телевизионных изображений. Впоследствии идея применения дифера была перенесена и на процесс квантования звуковых сигналов. Роль дифера, как средства борьбы с отрицательными явлениями, вызванными шумом квантования, заключается в следующем. Как уже упоминалось в разделе 2, шум квантования можно характеризовать как белый только для сигналов высокого уровня и сложного спектрального состава. В этом случае можно считать, сто статистическая связь между ошибками квантования отсутствует, и их величины могут принимать любые значения от +Q/2 до –Q/2 с равной вероятностью. Однако, начиная с некоторого предела, ошибка квантования перестает быть случайной некоррелированной величиной и начинает порождать новые гармонические составляющие и сложные искажения. Этот предел является функцией статистической связи между последовательно появляющимися ошибками, которая характеризуется коэффициентом корреляции К_корр. Для сигналов высокого уровня с широким спектром К_корр = 0,01, а для синусоидальной волны низкого уровня К_корр = 0,5. Однако К_корр = 0,5 и для сигналов высокого уровня с узкой полосой. Коэффициент корреляции начинает уменьшаться только с расширением полосы сигнала, и лишь в этом случае шум квантования начинает приобретать свойства белого. Здесь следует обратить внимание на то, что ошибка квантования во всех своих проявлениях имеет примерно одинаковую энергию, а ее субъективное восприятие изменяется лишь в силу изменения статистических характеристик самого сигнала.

Дифер – это случайный шумовой сигнал, размах которого в точности равен величине шага квантования и который имеет прямоугольную функцию плотности вероятности. Складываясь с синусоидальным сигналом низкого уровня, он приводит к тому, что результат квантования такого сигнала уже не будет выглядеть как периодическая последовательность прямоугольных импульсов, порождающая ряд нечетных гармоник высокого уровня, т.е. разрушает корреляционную связь между сигналом и шумом квантования. В случае удачного выбора дифера шум квантования в большей или меньшей степени приобретает свойства белого шума, что благоприятно сказывается на звучании цифровой фонограммы. Теоретически можно считать, что хорошо спроектированная 16-разрядная система а/ц- и ц/а-преобразования, использующая правильно подобранный дифер, способна обеспечить динамический диапазон звукового сигнала в 96 дБ. Качество звучания такой системы даже при наличии некоторых искажений, обусловленных несовершенством элементной базы, удовлетворит потребности самых взыскательных меломанов. Уровень шума в подобной системе должен быть постоянным, и какие-либо искажения, связанные с его наличием, на слух заметны быть не должны. Однако создание шумоподобного сигнала со строго прямоугольной функцией плотности вероятности и ее размахом, в точности равным величине шага квантования – задача сама по себе непростая и, несмотря на многочисленные исследования и эксперименты в этой области, не всегда приводит к планируемому разработчиками высокому результату.

До сих пор мы рассматривали системы аналого-цифрового преобразования сигналов, использующие линейную шкалу квантования. Такие системы по всем объективным показателям должны в наибольшей степени отвечать условиям максимально достижимой точности преобразования аналоговых величин в соответствующие им цифровые эквиваленты. Тем не менее, специфика передачи звуковых сигналов, рассматриваемая в данном разделе, позволяет взглянуть на процесс аналого-цифрового преобразования, а также на характер и величины связанных с ним погрешностей квантования, несколько с иной точки зрения, которая в других условиях и для других сигналов может оказаться совершенно неприемлемой. В свете вышесказанного следует обратить самое пристальное внимание на системы аналого-цифрового преобразования звука, в которых используется нелинейная зависимость выходного сигнала квантователя s_вых(t) = F(x) от величины к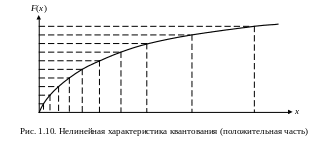 вантуемого сигнала s(t) (рис. 1.10).

Из рисунка видно, что нелинейность подобного рода систем выражается в том, что на начальном участке характеристики квантования, там, где входной сигнал невелик, шаг квантования выбирается небольшим, но по мере роста уровня входного сигнала он постепенно увеличивается, достигая наибольших значений в области максимального размаха входного воздействия. Такой способ преобразования позволяет получить достаточно высокое отношение сигнал/шум даже при очень слабом входном сигнале. Увеличение же уровня шума квантования на конечном участке характеристики квантования не столь существенно, поскольку этот шум маскируется высоким уровнем самого входного сигнала и делает его незаметным на слух.

Система квантования с характеристикой, подобной представленной на рис. 1.10, является, по сути, компрессором, сжимающим динамический диапазон звукового сигнала перед записью. Соответственно, система воспроизведения должна иметь в своем составе блок экспандера с характеристикой, обратной характеристике компрессора.

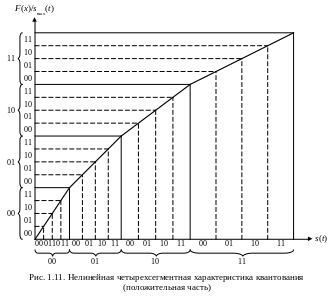
Сложностью в данной ситуации является то, что нелинейную систему с плавной характеристикой очень сложно реализовать физически. Поэтому в реальных системах нелинейного кодирования плавная кривая аппроксимируется линейно-ломаной линией, состоящей из нескольких отрезков, в пределах которых шаг квантования постоянен. Такие отрезки называются сегментами квантования. На рис. 1.11 представлена характеристика квантования, где таких сегментов – четыре. При переходе от сегмента с меньшим номером к сегменту с большим номером шаг квантования увеличивается вдвое. Число уровней квантования в пределах каждого сегмента одинаково и равно степени 2. На рис. 1.11 каждый из сегментов включает в себя четыре (2²) уровня квантования. Такие соотношения между размерами шага квантования и количеством уровней квантования предельно облегчают процесс кодирования значений отсчетов. Состоит он в следующем.

Левую позицию в коде выборки занимает символ, характеризующий полярность данного отсчета (0 или 1). Затем кодируется номер сегмента, в пределах которого находится мгновенное значение уровня входного сигнала. На рис. 1.11 сегментов всего четыре, т.е. для кодирования их номеров достаточно всего двух разрядов. Эти два разряда размещаются в коде отсчета справа от знакового разряда (старший разряд слева, младший – справа). После этого кодируется номер интервала квантования данного сегмента, в пределах которого находится уровень входного сигнала. На рис. 1.11 каждый сегмент включает в себя четыре интервала квантования, значит для кодирования номеров этих интервалов также достаточно двух разрядов. Общее число разрядов получается равным пяти, причем структура кода отсчета выглядит следующим образом: первый разряд – знаковый, он определяет полярность выборки входного сигнала; два последующих – это номер сегмента и последние два – номер интервала квантования.

В итоге, если считать уровень шума квантования равным ±Q₁/2, где Q₁ – шаг квантования в пределах первого сегмента, а максимальный размах входного сигнала пересчитать в количество уровней Q₁, то динамический диапазон пятиразрядного выходного сигнала при данном способе нелинейного кодирования получится равным

или в децибелах

D (дБ) = 20 lg120 ≈ 42 дБ

Если при том же шаге Q₁ квантование было бы линейным пятиразрядным, то

D (дБ) = 5·6 + 2 = 42 дБ.

Выигрыш очевиден. Из чего также следует, что другим полезным свойством нелинейного квантования, помимо лучшей передачи слабых сигналов, является возможность сокращения количества информации, необходимой для кодирования звукового сигнала с одним и тем же динамическим диапазоном.

Однако кроме очевидных преимуществ, нелинейное квантование имеет и очевидные недостатки. В частности, слабые сигналы (или обертоны) на фоне сильных сигналов (на участках характеристики с большим шагом квантования) могут сильно искажаться или даже пропадать совсем. Поэтому в высококачественных звуковых системах предпочитают использовать все же линейное квантование с высокой разрядностью.

Тем не менее, там, где требования к качеству звука не столь критичны, нелинейные системы находили и продолжают находить широкое применение.

Характеристика нелинейного квантования аналогового сигнала x = s(t) задается с помощью функции F(x), которая может отражать один из двух принятых на практике законов сжатия: μ-закон или А-закон. Формула для μ-закона имеет вид

(1.23)

где x – входной сигнал;

F(х) – выходной сигнал;

μ – фиксированный коэффициент, определяющий степень сжатия.

Формула, выражающая А-закон, выглядит следующим образом

(1.24)

и

(1.25)

Степень сжатия зависит от показателей μ и А и увеличивается с их увеличением. Характеристику нелинейного квантования принято обозначать буквой и двумя цифрами. Например, запись А75,2/11 означает, что характеристика квантования аппроксимируется по А-закону при А = 75,2 с помощью 11 сегментов. Запись μ10/16 означает, что используется характеристика квантования, соответствующая μ-закону сжатия при μ = 10 и состоящая из 16 сегментов.

Квантование в соответствии с μ-законом используется в системах цифровой связи и радиовещания Японии и Северной Америки, а в соответствии с А-законом – в Европе.