1. Вынужденные колебания материальной точки. Резонанс.

Колебания, происходящие под действием внешней периодической силы, называются вынужденными колебаниями. Внешняя периодическая сила, называемая вынуждающей, сообщает колебательной системе дополнительную энергию, которая идет на восполнение энергетических потерь, происходящих из-за трения. Если вынуждающая сила изменяется во времени по закону синуса или коси­нуса, то вынужденные колебания будут гармоническими и незатухающими.

В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из со­стояния равновесия), в случае вынужден­ных колебаний система поглощает эту энергию от источника внешней периодической силы непрерывно. Эта энергия восполняет потери, расходуемые на пре­одоление трения, и потому полная энергия колебательной системы no-прежнему ос­тается неизменной.

Частота вынужденных колебаний равна частоте вынуждающей силы. В случае, когда частота вынуждающей силы υ совпадает с собственной частотой колебательной системы υ₀, происходит рез­кое возрастание амплитуды вынужденных колебаний — резонанс. Резонанс возникает из-за того, что при υ = υ₀  внешняя сила, действуя в такт со свободными колебаниями, все время сонаправлена со скоростью колеблющегося тела и совершает по­ложительную работу: энергия колеблющегося те­ла увеличивается, и амплитуда его колебаний становится большой. График зависимости амплитуды вынужденных колебаний А_т от частоты вынужда­ющей силы υ  представлен на рисунке, этот график называется резонансной кривой:

Явление резонанса играет большую роль в ря­де природных, научных и производственных процессов. Например, необходимо учитывать явление резонанса при проектировании мостов, зданий и других сооружений, испытывающих вибрацию под нагрузкой, в противном случае 

1)Движение мат.точки называется вынужденным если на ряду с востанавливающей силой на неё действует возмущающая сила.

 С целью упрощения будем считать, что возмущающая сила изменяется по гармоническому закону.

Явление сильного возрастания амплитуды при совпадении частоты возмущающей силы с частотой собственных колебаний называется резонансом.

2. Главные оси и главные моменты инерции. Свойства главных осей и главных центральных осей инерции

Поскольку уравнение не содержит координат первой степени, то его центр совпадает с началом координат. Три оси симметрии эллипсоида инерции называются – главными осями инерции относительно точки 0, а момент инерции относительно осей – главным моментом инерции.

Если выбрать систему координат так, что бы оси совпадали с главными осями инерции механ. сист, то уравнение эллипса примет вид: J^*_x X²_* + J^*_y Y²_* + J^*_z Z²_* = 1

Каждой точке соотв. свой эллипс инерции и если он известен, то можно найти момент инерции относительно любой оси, проходящей через данную точку. Эллипсоид, соотв. центру масс тела называется центральным эллипсоидом инерции, а его оси симметрии главными центральными осями инерции.

Если известны главные центры моментов инерции, то можно построить центр эллипсоид. инерции, а отсюда следует определение: моментом инерции относительно любой оси, проходящей через центр масс системы

2. Две основные задачи динамики.

Первая задача динамики.

По заданному движению точки определить силу.

- уравнения движения точки

Решается методом дифференцирования.

Вторая задача динамики.

Решение второй задачи динамики составляет основное содержание всех разделов динамики.

По заданным силам определить движение точки. Задача решается методом интегрирования.

Если сила зависит только от t или только от x или V, то можно пользоваться следующими указаниями:

1) составить диф.уравнение движения точки:

а) начало координат совмещать с началом движения точки (или с её равновесным положением);

б) если движение по прямой, то одну из осей направить в сторону движения точки;

в) точку изобразить с приложенными силами в произвольном положении;

г) составить диф.уравнение в проекции на ось.

2) интегрирование диф.уравнения.

Замена переменных.

если

если

Диф.уравнение решать методом разделения переменных(кроме задач на колебания).

3) интегралы брать неопределёнными, учитывая постоянные интегрирования, найденные из начальных условий.

4) анализ движения точки.

4. Движение тел в воздухе при наличии сопротивления, пропорционального квадрату скорости.

При движении тел в газах в частности в воздухе при скорости до 300 м\с сила сопротивления пропорциональна квадрату скорости, т.е. где x- const   

4. Дифференциальное уравнение относительного движения материальной точки.

1)Введем 2 вектора

численно равные произведениям

и направленные противоположно ускорениям

Эти векторы назовём переносной и кориолисовой силами инерции.

Дифф.ур-я относительного движения мат.точки.

6. Диф.уравнения движения материальной точки.

При плоском движении точки:

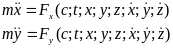
Если тело движется прямолинейно, то

В проекциях на естественные оси координат:

, где S- закон движения точки по траектории.

7. Дифференциальные уравнения движения механической системы. Теорема о движении центра масс системы.

Уравнения, из которых можно определить закон движения каждой точки системы, называются дифференциальными уравнениями движения системы в векторной форме.

Запишем теорему о движении центра масс системы:

Проектируя это уравнение на оси системы координат, получим:

, ,

эти уравнения называются уравнениями движения механ. сист. в вектр. ф – ме.

Теорема о движении центра масс системы.

Произведение массы системы на ускорение ее центра массе равно главному вектору внешних сил.