17. Счетчики. Синхронные и асинхронные счетчики

Лекция 6. Свои лекции.

Счётчик числа импульсов — устройство, на выходах которого получается двоичный (двоично-десятичный) код, определяемый числом поступивших импульсов. Счётчики могут строиться на двухступенчатых D-триггерах, T-триггерах и JK-триггерах.

Основной параметр счётчика — модуль счёта — максимальное число единичных сигналов, которое может быть сосчитано счётчиком. Счётчики обозначают через СТ (от англ. counter).

Счетчики и делители подразделяются на асинхронные и синхронные. У синхронных счетчиков все разрядные триггеры синхронизируются параллельно одними и теми же синхроимпульсами, поступающими из источника этих импульсов. Асинхронные счетчики имеют последовательную синхронизацию, т.е. каждый последующий разрядный триггер синхронизируется выходными импульсами триггера предыдущего разряда. Асинхронные счетчики иногда называют последовательными, а синхронные счетчики - параллельными.   Синхронные счетчики, в свою очередь, подразделяются на параллельно-синхронные и последовательно-синхронные. Параллельные счетчики имеют более высокую скорость счета, чем асинхронные.

18. Декадные счетчики.

Цифр электроника 280стр.

Большинство счетчиков работают в обычном двоичном коде, то есть считают от 0 до (2N–1), где N - число разрядов выходного кода счетчика. Например, 4-разрядный счетчик в режиме прямого счета будет считать от 0 (код 0000) до 15 (код 1111), а 8-разрядный - от 0 (код 0000 0000) до 255 (код 1111 1111). После максимального значения кода счетчик по следующему входному импульсу переключается опять в 0, то есть работает по кругу. Если же счет - инверсный, то счетчик считает до нуля, а дальше переходит к максимальному коду 111...1.

Имеются также двоично-десятичные счетчики, предельный код на выходе которых не превышает максимального двоично-десятичного числа, возможного при данном количестве разрядов. Например, 4-разрядный двоично-десятичный счетчик в режиме прямого счета будет считать от 0 (код 0000) до 9 (код 1001), а затем снова от 0 до 9. А 8-разрядный двоично-десятичный счетчик будет считать от 0 (код 0000 0000) до 99 (код 1001 1001). При инверсном счете двоично-десятичные счетчики считают до нуля, а со следующим входным импульсом переходят к максимально возможному двоично-десятичному числу (то есть 9 - для 4-разрядного счетчика, 99 - для 8-разрядного счетчика). Двоично-десятичные счетчики удобны, например, при организации десятичной индикации их выходного кода. Применяются они гораздо реже обычных двоичных счетчиков.

19. Счетчики Джонсона. Устройство, принцип действия, назначение.

На базе регистров сдвига можно построить кольцевые счетчики - счетчики Джонсона. Счетчик Джонсона имеет коэффициент пересчета, вдвое больший числа составляющих его триггеров. В частности, если счетчик состоит из трех триггеров (m=3), то он будет иметь шесть устойчивых состояний. Счетчик Джонсона используется в системах автоматики в качестве распределителей импульсов и т.д.

  Таблица состояний счетчика Джонсона (рис. 3.29) содержит 2m (m - количество триггеров в составе регистра) строк и m-столбцов. Количество разрядов счетчика определяется количеством триггеров (рис. 3.29). Рассмотрим схему трехразрядного счетчика Джонсона, выполненного на базе D-триггеров (регистр сдвига реализован на D-триггерах). Для построения кольцевого счетчика достаточно соединить инверсный выход последнего триггера регистра (последнего разряда) с входом “D” (с входом, предназначенным для ввода последовательной информации) первого триггера.

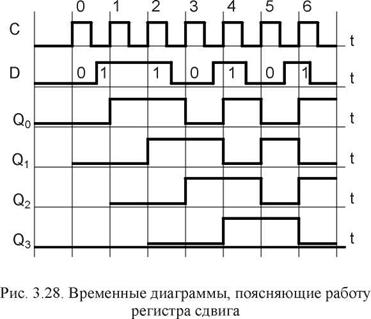
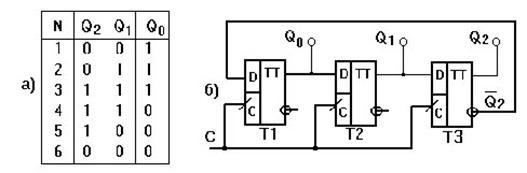
Рис. 3.29. Таблица состояний а) и схема б) счетчика Джонсона на трехразрядном регистре сдвига

 

 

  Предположим, что вначале все триггеры находятся в состоянии “0”, т.е. Q₀= Q₁=Q₂=0. При этом на входе “D” первого триггера присутствует уровень “1”, т.к  =1. Первым синхроимпульсом в триггер Т1 запишется “1”, вторым - единица запишется в первый триггер, из первого - во второй и т.д. до тех пор, пока на всех выходах регистра не будет “1”. После заполнения регистра единицами, на инверсном выходе триггера Т3 появится  =0 и четвертым синхроимпульсом в Т1 запишется логический “0” (рис. 3.29, б).

  После поступления последующих трех синхроимпульсов регистр обнуляется и на его вход “D” снова подается уровень “1”. Таким образом, цикл повторения состояния кольцевого счетчика состоит из шести тактов синхросигнала. Как видим, при работе в начале от первого триггера до последнего триггера распространяется “волна единиц”, а затем “волна нулей”. Код, в котором работает счетчик Джонсона, называют кодом Либау-Крейга.

Счетчики Джонсона широко используются в делителях частоты импульсов, генераторах случайных чисел, в устройствах памяти и так далее.