27.Сохранение связности непрерывными отображениями. Теорема о промежуточных значениях.

Т1. Непрерывный образ связного пр-ва - связн.(т.е если f:X->Y непр. и сюръект. и Х св., то У – св.)

док. (от противного)

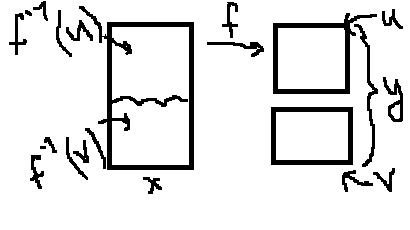Т2(о промеж. знач) Пусть Х-Т.П Если непр ф-ия f:X-> опр. на св. пр-ве Х принимает значения (a<b), то она принимает и все значения между ними.

док.(от противного)

28.Сохранение связности непрерывных отображений. Теорема о промежуточных значениях

Теорема 1. Непрерывный образ связного пространства- связен(т.е. если f : X → Y непрерывно и сюрьективно и Х – связно, то Y - свсвязно). X U

□ (от противного) Y – несвязное. Т.е. Y =u U v f^-1(u) f

Ø≠U ϵ_op Х Ø≠Vϵ_op X u v = Ø X = f^-1(u) U f^-1(V) Ø≠ f^-1(u)ϵ_op X

Ø≠ f^-1(v)ϵ_op X f^-1(u) f^-1(v)=Ø ?! ▪ f^-1(v)

V

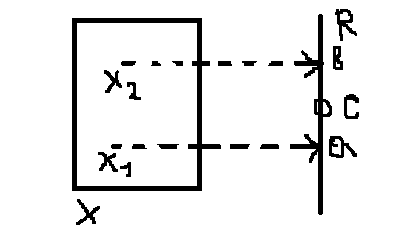
Т2. (О промежуточных значениях)

Пусть X – Т.П. Если непр. Ф-ия. f : X→ опр. На св. пр-ве.

X принимает значения a, в ϵ R (a < в) , то она принимает и все значения между ними.

X₁

X₂

F→ R

c

x □(от противного) ɏx ϵ X f(x)≠c X= f^-1 (]-∞;c[) U = f^-1(]c;+∞[). Ø = f^-1 (]-∞;c[) ϵ_op R Ø = f^-1(]c;+∞[) ϵ_op R f^-1 (]-∞;c[) Ω = f^-1(]c;+∞[) = Ø ?! ▪

29 Линейно связные пространства. Связь между связностью и линейной связностью. Сохранение линейной связности непрерывными отображениями. Примеры линейно связных пространств.

Опр 1 ТП Х называется линейно связным если ɏ х, у ϵ X существует непрерывное отображение f: [0, 1]->X| f(0)=x; f(1)=y.

Отобр f называется непрерывным путём, соед х и у, а мн-во f( [0, 1]) – носителем пути.

Утверждение 1. Любое линейно-связное Т.П. Х –связно.

□Доказательство следует из того, что ɏ х,y X соединяющие их свойство множество, а именно носителем соед. их пути▪

Утв.2 Непрерывное отображение линейно связного пространства линейно связно. Док-во. Пусть Х, Y – ТП, f:Х->Y непр и сюръективно. Х линейно связно, покажем что У линейно связно.

Пусть у₁, у₂ ϵУ, существуют х₁, х₂ ϵХ : f(x₁)=y₁, f(x₂)=y₂, существует непр ϕ:[0;1]->Y | ϕ(0)=x₁, ϕ(1)=x₂. Пусть g=f* ϕ =>g:[0;1]->Y непр. g(0)=y₁, g(1)=y₂.

Примеры. 1) линейно связно.

Пусть х,у их радиус векторы. Отобр. :[0; 1] : t = +t*( - )

 непр. (0)=х, (1)=у. Носитель пути -отрезок. Аналогично: п. св. Dⁿ(a,r), Bⁿ(a,r)

2) в Rⁿ S^n-1(c,r)-л.св. (n ≥2)-сфера r=2 ; Пусть с=(0,….,0)

Р-м, а, в ϵS¹(c,r) ϕ:[0;1]→S¹(c,r) ϕ(t)=(rcos(α+t(p-α)),rsin(α+t(β-α)))

n>2 Р-м а,в ϵ S^n-1(c,r) Ǝ двум. пл-ть. П проходящая через точки а, в,с ; ПΩ S^n-1 (с, r)-окр.в П

Любое линейно связное ТП связно

Док-во. Следует из того что ɏ х, у ϵ X существует содержащее их связное множество, а именно носитель.