
- •5. Замкнутые множества в топологическом пространстве и их свойства.
- •7. Хаусдорфовы пр-ва.
- •8.Предел последовательности.
- •9.Замыкание мн-ва
- •1) Если
- •2) Если
- •13.Всюду плотные множества в топологических пространствах. Сепарабельность. Связь между сепарабельностью и второй аксиомой счетности. Пример: существование счетной базы в
- •14 . Сравнение топологий.
- •15. Сравнение метрических топологий. Критерий топологической эквивалентности метрик
- •16. Непрерывное отображение топологических множеств. Определения. Примеры. Теорема о непрерывности композиции
- •17. Критерий непрерывности отображений топологических пространств.
- •18. Сужение отображение на подпространство топологического пространства и его непрерывность (2 теоремы)
- •19.Операции над вещественно-значимыми непрерывными функциями
- •20.Секвенциально непрерывные отображения топологических пространств.
- •21.Понятие гомеоморфизма. Пример: стереографическая проекция. Пример непрерывной биекции, не являющейся гомеоморфизмом
- •22.Метод введения топологии с помощью базы.
- •23 Определение топологии произведения топологических пространств. Теорема о метричности этой топологии. Примеры.
- •25. Проектирование на произведении топологических пространств и их непрерывность отображения в произведении.
- •27.Сохранение связности непрерывными отображениями. Теорема о промежуточных значениях.
- •28.Сохранение связности непрерывных отображений. Теорема о промежуточных значениях
- •29 Линейно связные пространства. Связь между связностью и линейной связностью. Сохранение линейной связности непрерывными отображениями. Примеры линейно связных пространств.
- •30.Связность замыкания связного множества. Свойства веера.
- •Связные компанеты
- •31) Связные компоненты топологического пространства и их свойства. Пример: связные компоненты q ( как подпространства r)
- •32) Понятие компактного топологического пространства. Характеристика компактности через центрированные семейства замкнутых множеств. Примеры.
- •33) Теорема о компактности произведения компактных пространств
- •34 Компактность замкнутого подпространства компактного пространства.
- •35 Сохранение компактности непрерывными отображениями. Теорема Вейерштрасса. Пример ограниченного непрерывного отображения из r в r, не имеющего ни точки максимума, ни точки минимума
- •36 Теорема о непрерывной биекции компактного пространства на хаусдорфово. Пример: граница выпуклого многоугольника на плоскости r2 гомеоморфна окружности
- •37.Полные метрические пространства. Примеры полных и неполных пространств. Полнота. Полнота подпространств.
- •38. Убывающие последовательности замкнутых множеств в полных метрических пространствах.
- •39.Вполне ограниченные метрические пространства. Связь между ограниченностью и вполне ограниченностью. Вполне ограниченные множества в (Rn, d) (d-евклидова метрика)
- •41 Теорема о связи между компактностью, полнотой и полной ограниченностью метрических пространств: доказательство того, что компактное метрическое пространство является полным и вполне ограниченным
- •42 Теорема о связи между компактностью, полнотой и полной ограниченностью метрических пространств: доказательство того, что полное и вполне ограниченное метрическое пространство компактно.
- •43. Критерий компактности полного метрического пространства.
- •44. Предельные точки множеств в тп. Критерий компактности метризуемого тп( последовательности и предельности).
- •45. Фактор-пространство тп по данному разбиению(1). Естественное отображение тп на его фактор-пространство и его свойства(2).
- •46.Понятие факторного отображения топологических пространств. Достаточные условия, при выполнении которых сюръективное непрерывное отображение является факторным.
- •47. Теорема о связи между конструкцией фактор-пространства и факторными отображениями. Пример фактор-пространства.
22.Метод введения топологии с помощью базы.
Если
 Утв.1
Пусть x
– непустое мн-во β -семейств.
Подмн-во
мн-ва x,
удовл. усл.
В1) Uβ=xu
В2)
Утв.1
Пусть x
– непустое мн-во β -семейств.
Подмн-во
мн-ва x,
удовл. усл.
В1) Uβ=xu
В2)
![]() V1,
V2
β
и
x
V1
∩ V2
∃
U
β | x
V
⊆
V1
∩ V2
тогда
∃
единственная топология
V1,
V2
β
и
x
V1
∩ V2
∃
U
β | x
V
⊆
V1
∩ V2
тогда
∃
единственная топология ![]() на мн-ве X,
такая что β
является базой
пр-ва (x,
)
□ Рассм. семейство
опр. по правилу:
∅
,
U
x
U
∃
U
β
| x
V
⊆
U
Покажем, что
- топология на X.
□
01) ∅
,
x
(Из В1)
02) Покажем, что пересечение
конечн. совокуп. мн-в из
принадл.
(□
индук. по числу n
мн-в пересек. совокупн.)
n=1
– выполн.
Пусть утв. верно для сов-тей
с числом мн-в n=2.
Покажем, что оно верно для совокуп. с
числ. n=k+1
Пусть
U=U1∩…∩Uk+1
, где Ui
, i=1,k+1
Обозн.
U*=
U1∩…∩Uk
, U*
U=
U*
∩ Uk+1
, пусть x
U
∃
V1
β | λ
U1
⊆
U*
∃
V2
β| x
U2
⊆
Uk+1
∃
U
β| x
U
⊆
V1∩
V2,
V
⊆
U
=> U
на мн-ве X,
такая что β
является базой
пр-ва (x,
)
□ Рассм. семейство
опр. по правилу:
∅
,
U
x
U
∃
U
β
| x
V
⊆
U
Покажем, что
- топология на X.
□
01) ∅
,
x
(Из В1)
02) Покажем, что пересечение
конечн. совокуп. мн-в из
принадл.
(□
индук. по числу n
мн-в пересек. совокупн.)
n=1
– выполн.
Пусть утв. верно для сов-тей
с числом мн-в n=2.
Покажем, что оно верно для совокуп. с
числ. n=k+1
Пусть
U=U1∩…∩Uk+1
, где Ui
, i=1,k+1
Обозн.
U*=
U1∩…∩Uk
, U*
U=
U*
∩ Uk+1
, пусть x
U
∃
V1
β | λ
U1
⊆
U*
∃
V2
β| x
U2
⊆
Uk+1
∃
U
β| x
U
⊆
V1∩
V2,
V
⊆
U
=> U
03)Пусть
U=VUt
, где где
t
Ut
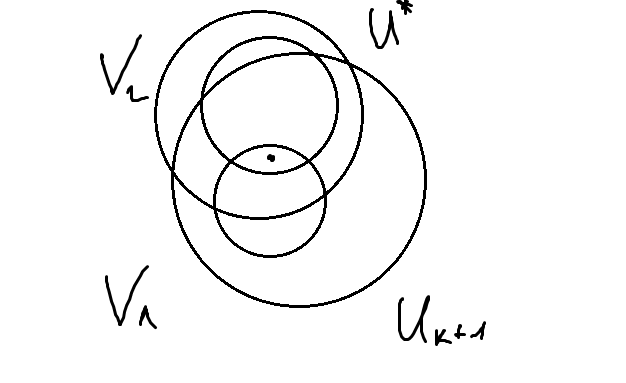
Покажем, что U , рассмотрим т.к. ∃ t0 | x U0 ∃V β|| x V ⊆ U0 V ⊆ U ▪ β – база пр-ва (x, )
Лемма: Пусть
даны т.п.
 ,
x=
,
x= Семейство βn
подмн-в мн-ва x, сост. Из
всех мн-в вида
Семейство βn
подмн-в мн-ва x, сост. Из
всех мн-в вида
 , где
i=1,n
Ui⊆xi
удл.
Условиям B1,
B2.
□B1:
βn
B2:
βn
, где
i=1,n
Ui⊆xi
удл.
Условиям B1,
B2.
□B1:
βn
B2:
βn
 βn
βn
 =
= βn ▪
βn ▪
23 Определение топологии произведения топологических пространств. Теорема о метричности этой топологии. Примеры.
Опр. Пусть даны т.п. , x= Топологией произведения на Х наз. топология r базу которой образует сем-во βn
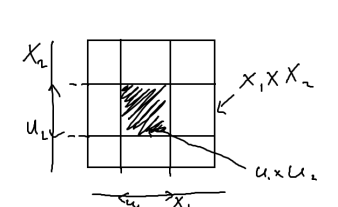 Утв.
Пусть
– т.п. x=
Если каждое из пр-в x:
метризуемо метрикой p,
то х метриз. метрикой p(x,y)=max
pi(xi,yi)
Утв.
Пусть
– т.п. x=
Если каждое из пр-в x:
метризуемо метрикой p,
то х метриз. метрикой p(x,y)=max
pi(xi,yi)
x=
y=
 □
1)покажем, что p-метрика
М1),
М2) очевидно
М3) p(x,y)
≤p(x,z)+p(z,y)
i=1,n
pi(xi,yi)
≤pi(xi,ei)+pi(zi,yi)
≤p(x,z)+p(z,y)
p(x,y)
≤p(x,z)+p(z,y)
2)Вид
шара, пусть a=(ai…ak)
X,
ε>0
x=(x1…xn)
βp(a,
ε)
p(a,x)<
ε
□
1)покажем, что p-метрика
М1),
М2) очевидно
М3) p(x,y)
≤p(x,z)+p(z,y)
i=1,n
pi(xi,yi)
≤pi(xi,ei)+pi(zi,yi)
≤p(x,z)+p(z,y)
p(x,y)
≤p(x,z)+p(z,y)
2)Вид
шара, пусть a=(ai…ak)
X,
ε>0
x=(x1…xn)
βp(a,
ε)
p(a,x)<
ε
 β(a,
ε)=
βp1(a1,
ε)*…
βpn(an,
ε)
Вывод:
a
X,
ε>0
βp(a,
ε)
βn
3)Покажем,
что
P=
n
пок.
p
пусть
G
P,
когда
a
G
∃
εa>0
| βp
(a,
εa)
G,
Т.к. все βp
(a,
εa)
βn
и G=
∪
βp(a,
ε0)
G
n
Покажем
n
⊆
P
, пусть G
p
, рассм.
a=(a1…an)
G
∃
|
a
β(a,
ε)=
βp1(a1,
ε)*…
βpn(an,
ε)
Вывод:
a
X,
ε>0
βp(a,
ε)
βn
3)Покажем,
что
P=
n
пок.
p
пусть
G
P,
когда
a
G
∃
εa>0
| βp
(a,
εa)
G,
Т.к. все βp
(a,
εa)
βn
и G=
∪
βp(a,
ε0)
G
n
Покажем
n
⊆
P
, пусть G
p
, рассм.
a=(a1…an)
G
∃
|
a
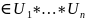 ⊆
G
Ui⊆xi
i=1,n
i=1,n
∃
εi>0|
βp(ai,
εi)
⊆
Ui
ε=min{ε1…εn},
тогда βp(a,
ε)=
⊆
G
Ui⊆xi
i=1,n
i=1,n
∃
εi>0|
βp(ai,
εi)
⊆
Ui
ε=min{ε1…εn},
тогда βp(a,
ε)=
 ⊆
⊆G▪
Примеры:
1)На
ℝn=
⊆
⊆G▪
Примеры:
1)На
ℝn= n=
n
μ(x,y)=max|xi-yi|
n(из
утв.2)
μ~d=>
n=
n
2)В
ℝn
рассм. фигуры
П:
n=
n
μ(x,y)=max|xi-yi|
n(из
утв.2)
μ~d=>
n=
n
2)В
ℝn
рассм. фигуры
П: Где
ai<bi
i=1,n
П=
Где
ai<bi
i=1,n
П= Топология произведения на П сов. с
топ., из ℝn
24
Сходимость
последовательностей в произведении
топологических пространств.
Утв.
Пусть x=
,
где
-т.п.
λ=(x1…xn)
X
(X(k))k=1
послед. в х-точек, х(к)=(х1(к)
… хn(k))
x(k)a->
x
в x
i=1,n
xi(k)->xi
в xi
□=>)fix
i
≤
n
Рассм.
окр. U
топ. xi
в Xi
Рассм.
G=
Топология произведения на П сов. с
топ., из ℝn
24
Сходимость
последовательностей в произведении
топологических пространств.
Утв.
Пусть x=
,
где
-т.п.
λ=(x1…xn)
X
(X(k))k=1
послед. в х-точек, х(к)=(х1(к)
… хn(k))
x(k)a->
x
в x
i=1,n
xi(k)->xi
в xi
□=>)fix
i
≤
n
Рассм.
окр. U
топ. xi
в Xi
Рассм.
G= -
опр. точки х в Х
∃
p
ℕ |
k
≥
p
x(k)
G
Тогда
k≥p
x1(k)
-
опр. точки х в Х
∃
p
ℕ |
k
≥
p
x(k)
G
Тогда
k≥p
x1(k) <=)Рассмотрим
окр. G=
точки х в Х
i=1,n
∃
pi
ℕ |
k≥pi
xi(k)
Ui
Пусть
p=max
{p1…pn};
k≥p
x(k)
G
▪
<=)Рассмотрим
окр. G=
точки х в Х
i=1,n
∃
pi
ℕ |
k≥pi
xi(k)
Ui
Пусть
p=max
{p1…pn};
k≥p
x(k)
G
▪
25. Проектирование на произведении топологических пространств и их непрерывность отображения в произведении.
Опр.1
Пусть Х=Х1*…*Хn,
где Х1…Хn
– ТП. fix
i Отобр.
pi:
X
Отобр.
pi:
X Xi
так. что
x=(x1,…xn)
xi
наз. i-ым
проектированием
Xi
так. что
x=(x1,…xn)
xi
наз. i-ым
проектированием
Утв.
2 Пусть
Х= Х1*…*Хn,
где Х1…Хn
– ТП.
i
проектирование pi:
X
Xi
непрерывно.
док. пок. что
 I
pi-1(W)
I
pi-1(W) p1(W)=X1*….Xi1*W*Xi+1*….*Xn
p1(W)=X1*….Xi1*W*Xi+1*….*Xn
26.
Связные пространства, Простейшие хар-ки
несвязан. Примеры : связность отрезка и несвязность ℚ(как
подпростр. ℝ)
и несвязность ℚ(как
подпростр. ℝ)
Опр.
ТП. Х наз. несвязным если его можно
представить в виде двух непустых
непересекающихся открытых мн-в(т.е. в
виде X где U
где U .
Х наз. связным если оно не явл. несвязным.
.
Х наз. связным если оно не явл. несвязным.
Утв. ТП Х след. утв. эквивалентны
а) Х несвязно
б)
Х можно представить в виде объединения
2-х непустых непересек. замкн. подмн-в(
т.е в виде X=F
в) В Х нетривиальное (непустое и отличное от всего Х) открыто- замкнутое мн-во
док.
а б)
Пусть Х=U
б)
Пусть Х=U , где ,
, где ,

б
в)
пусть Х= )
)
в
а)
пусть А⊆
Примеры:
2)Отрезок связн.
связн.
Обозначение
для
 док.(от противного). Доп. [a,b]=U
док.(от противного). Доп. [a,b]=U

Пусть
с-середина [a,b].
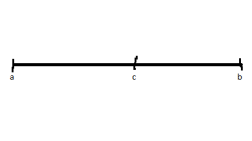 Хотя бы 1 из 2-х отрезков [a,c]или
[c,b]
пересекается и с U
и с V.
Хотя бы 1 из 2-х отрезков [a,c]или
[c,b]
пересекается и с U
и с V.
Действ.
пусть напр. а [a1,b1
]
[a1,b1
]
Построим по инд. послед. отрезков
[a1,b1] …
[an,bn]
…
Каждый из которых пересек. и с U
и с V
для которых вып. bn-an=
…
[an,bn]
…
Каждый из которых пересек. и с U
и с V
для которых вып. bn-an=
Пусть
z
– общая точка этих отрезков. Пусть, напр
z
 [an,bn]
[an,bn]
3)

![]()
в

