19.Операции над вещественно-значимыми непрерывными функциями
Пусть X-Т.П., f:X->ℝ, g:X->ℝ – непр. отобр.
Тогда непр. отображения;
А)
Г)fg
Б)
f,
Д)
если g(x)
0
x
X
В) |f| Е) max(f,g)
E)min(f,g)
Док-во
а) Пусть h=f+g. Рассмотрим ᗄт.x X, надо показать, что ᗄ ɛ>0 Ǝ окр. U т-ки X | ᗄxI U | h(x)-h(xI)|< ɛ
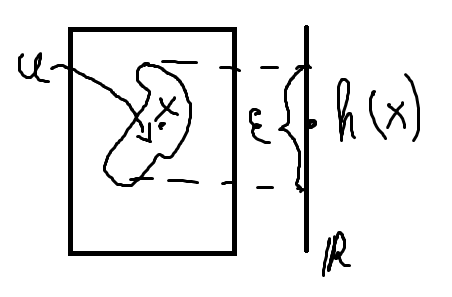
fix
ᗄ
ɛ>0. т.к. f –непр, Ǝ окр. V т-ки x | ᗄxI
V |f(x) – f(xI)|<
T.к. g- непр Ǝ
окр W т-ки x | ᗄxI
W |g(x)-g(xI)|
<
Пусть
U=V ∩ W. Тогда
ᗄxI
U |h(x)-h(xI)|
|(f(x)+g(x)-f(xI)-f(xI)|
|f(x)-f(xI)+|g(x)-g(xI)|<
ɛ
Замечание.
Предыдущее
утв. распространяется по индукции на
сумму, произведение max и min любого
конечного набора непрерывных функций.
20.Секвенциально непрерывные отображения топологических пространств.
Связь между непрерывностью и секвенциальной непрерывностью
Опр. Пусть X,Y –Т.П. Отображение f:X->Y наз секвенциально непрерывным, если ᗄx X и ᗄ посл.
точек пр-ва X
из Xn->X=>
f(xn)->f(x)
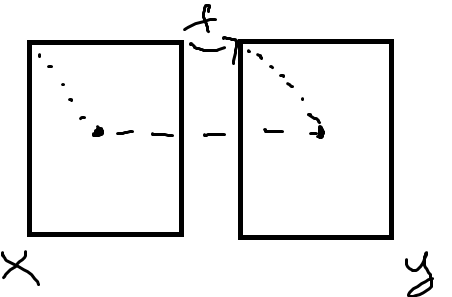
Утв. Пусть X,Y-Т.П. f:X->Y – отображения.
а) Если f непр., то f секв. непр.
б) Если X метризуемо и f секв. непр., то f-непр.
Док-во
а) Пусть f-непр => f-cекв. непр.
Пусть в X xn->x Покажем, что f(xn)->f(x) (в Y)
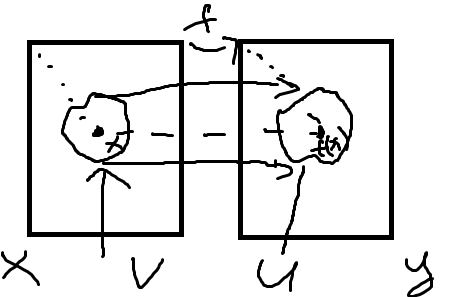
Ǝ окр V т-ки x | f(V) ⊆ U
Ǝ
p
| ᗄn
p
xn
V
Тогда ᗄn p f(xn) U, т.е. f(xn) ->f(x)
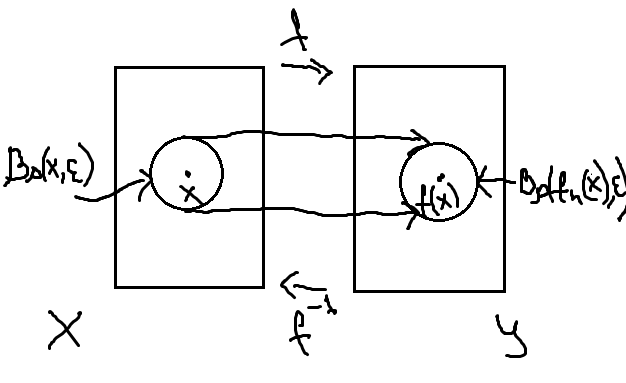
б) Пусть ρ-метрика согласованна с топологией пр-ва X От противного
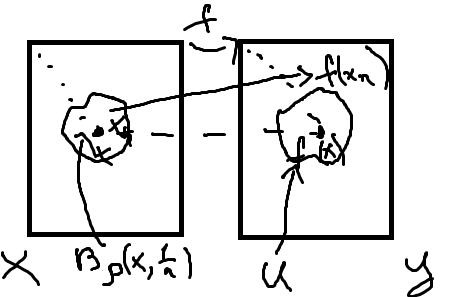
Допустим Ǝ x X | f – разр. в т. x, т.е. Ǝ окр U т-ки f(x) | ᗄокр V т-ки x вып. f(V) ⊈ U.
В
частности, ᗄn
Ǝ x1
Bp(x,
)|
f(xn)
⊈
U. Тогда xn->x,
но f(xn)
не -> f(x)
21.Понятие гомеоморфизма. Пример: стереографическая проекция. Пример непрерывной биекции, не являющейся гомеоморфизмом
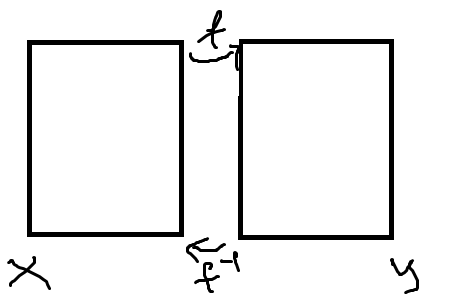
Опр. Пусть X, Y – Т.П . Отображение f : X → Y Называется гомеоморфизмом, если:
1) f-биекция
2) f-непр.
3) f-1: Y→X-непр
Если Ǝ гомеоморфизм f : X → Y то пр-ва X и Y называются гомеоморфными (X≈Y)
Замечание
1. Если X-ТП-
гомеоморфно подпр-ву В пр-ва Y, то говорим
что X гомеоморфно вкладывается в Y, а
гомеоморфизм f:X→В наз. Гомеоморфным
вложением пр-ва X в пр-во Y (X
Y).
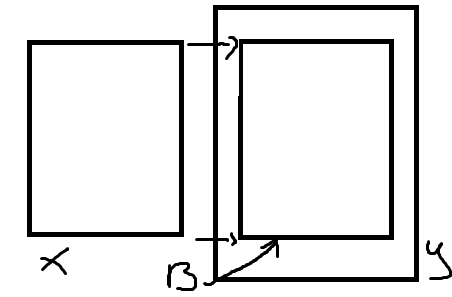
Замечание 2.
Пусть X, Y, Z – Т.П.
1)X≈X; id : X →X.
2)Если У≈X ,то и X≈Y.
3)Если X≈Y, Y≈Z, то и X≈Z.
Замечание 3.
Любая изометрия метрических пространств явл. гомеоморфизмом.
Примеры:
1) Пусть f : Rn→R-
аф. преобр.
непр.
f- непр. f-1- аф. пр-е => f-1 непр. f- гомеоморфно
Аф. Экв. Фигуры- гомеоморфны.
2)Любой интервал ]a, в[⊆ ℝ гомеоморфен ℝ
а в
R ]a, в[ ≈]0;1[
ϕ: ]0,1[→]а,b[ : t →a + t(b-а)
Пок.
что
≈ℝ
f : →ℝ ; f(t)=tg t
3)Любой шар пр-ва ℝn гомеоморфен ℝn Ǝ аф. преобразование, которое Bn(a,r) перев. В шар Bn с ц. в.т. о рад 1
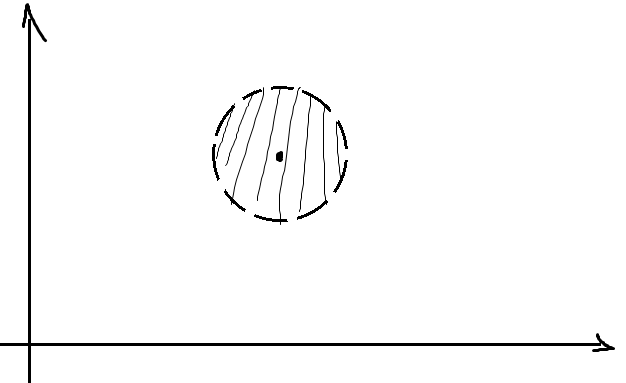
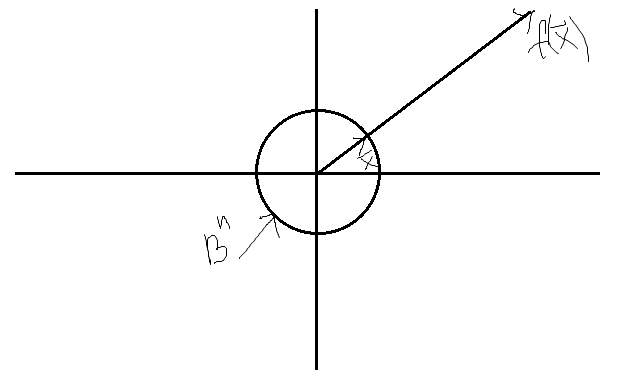
Bn≈ℝn;
f:Bn->ℝn:x.->
f-непр.;
=(x1,…,xn);
f(
)=(
-непр,
f-инъективно, пусть
⟹
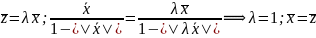
f-cюръективно,
рассмотрим
ℝn,
ищем x. | f(
)=
.
ищем в виде
,
𝜆>0
,
(
≠0,
𝜆>0)=>
=1
𝜆=1-𝜆||
||, α=
;
x.=
кончим прообраз. f-1-непрерывно.
4) Пусть M⊆ ℝ; p:M->ℝ непр. отобр.
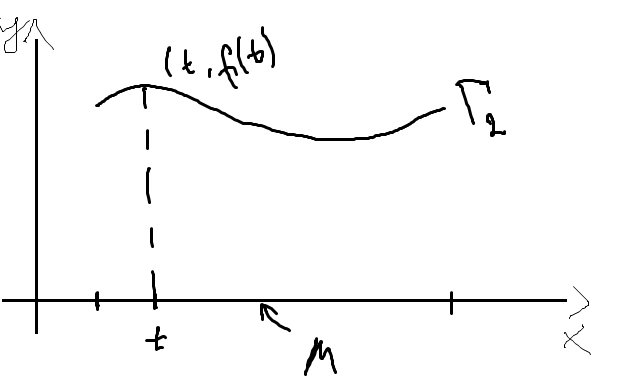
Рассмотрим на пл-ти ℝ2 фигуру Гf:y=f(x) покажем, что Гf≈M h:M->Гf; h(t)=(t,f(t)) h-гомеоморфно
4I) На пл-ти ℝ2 рассмотрим фигуру Ф:y=x2
f:ℝ->ℝ; f(x)=x2; Ф≈ℝ
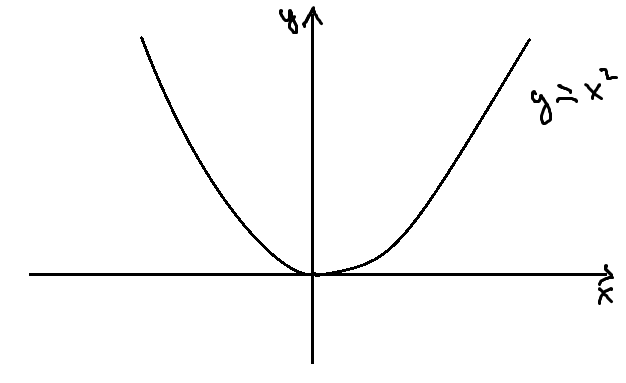
парабола гомеоморфна прямой
Рассмотрим
:
xy=1
x>0
f.:]0,
+
[->ℝ
график
.
(x)=
;
]0,+
[≈
Ф.
Заметим: ]0;+ [≈ℝ
Гомеоморфизм g:]0;+ [≈ℝ задается формулой g(x)=Ln x; Ф. ≈ℝ.
Ветвь гиперболы ≈ℝ
Парабола ≈ ветви гиперболы
5) Пусть M⊆ ℝ2; f:M->ℝ непр. отобр. Рассмотрим в ℝ3 фигуру Гf зад ур-ем z=f(x,y)
Гf≈М
h:M->Гf
h(x,y)=(x,y,f(x,y))
h – гомеоморфизм
5’)
В ℝ3
рассмотрим фигуру Ф: x2+y2-z2=-1
z 0
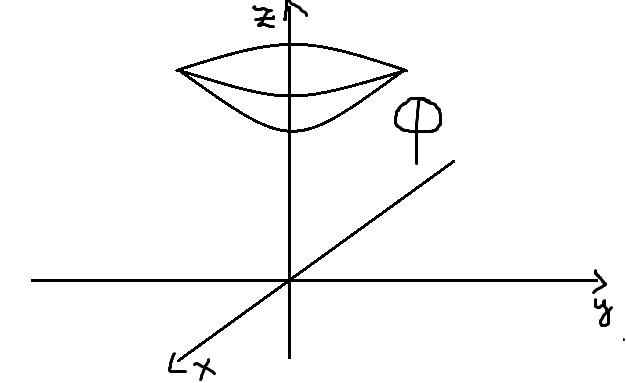
Фz=
Ф-гр. отобр f:ℝ2->ℝ опр. по правилу f(x,y)=
Ф≈ℝ2