16. Непрерывное отображение топологических множеств. Определения. Примеры. Теорема о непрерывности композиции

Опр непрерывного отображения

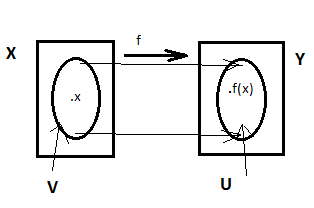
Пусть (Х,τ₁) и (Y,τ₂) – Т.П. Отображение F: Х—>Y называют непрерывным в т. х ϵ Х , если для любой окрестности U точки f(x) Ǝ окрестность V точки х ǀ f(V)c_ U. Отображение называется непрерывным, если оно непрерывно в каждой точке . Множество всех отображений из X в Y обозначатся C(X,Y). Если Y=R, то С(Х).

Замечание Пусть (Х,ρ₁) и (Y,ρ₂) – М.П. F: Х—>Y - непрерывно в т. х ϵ Х  для любого ε>0 Ǝ δ>0ǀ f(B_ρ1(x,δ)) c_ B_ρ2(f(x),ε) или: f - непрерывно в х  для любого ε>0 Ǝ δ>0ǀ для любого x’ ϵ X удовл. усл. Ρ₁(х,x’)<δ выполн ρ₂(f(x), f(x’))<ε

Примеры: 1) f:R —>R; f(x)=cos x

2) f:R —>R; f(x)=sin x

3)f:]0;+∞[ —>R; f(x)= ln x

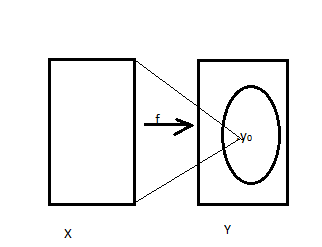
4) Пусть X,Y – Т.П. y₀ ϵY; Рассм F: Х—>Y , для любого xϵX f(x)= y₀; F – непрерывно

Непрерывность композиции

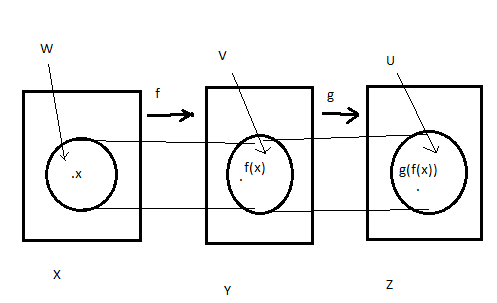
Утв1 Пуcть X,Y,Z – Т.П.; f: Х—>Y , g:Y—>Z – непрерывные отображения. Тогда g◦f:X—>Z – непрерывна.

▫ Рассмотрим для любой т. xϵX и для любой окрестности U точки( g◦f)(х) Ǝ окрестность V точки f(x) ǀg(V)c_U; Ǝ окресн W точки хǀf(W)c_V => g◦f(W)c_U ▪(конец)

17. Критерий непрерывности отображений топологических пространств.

Критерий непрерывности

Пусть X,Y – Т.П. f:X—>Y - отображение. Следующие условия эквивалентны:

1. F-непрерывно

2. Для любого Uc__opY:f^-1(U)c__opX

3. Для любого Fc__clY:f^-1(F)c__clX

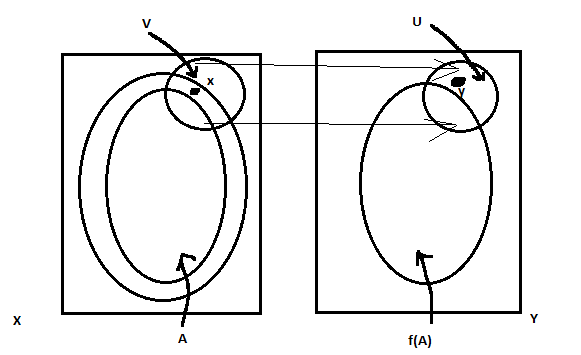
4. Для любого Ac_X:f(A^—)c_f(A)^—

▫ 1) =>4) Рассм для любого Ac_X. Пусть yϵ f(A^—) => Ǝ xϵ A^— ǀ f(x)=y. Рассм для любой окрестности U точки y Ǝ окрестность V точки x ǀf(v)c_U. т.к. xϵ A^— , V∩A≠ø => U∩f(A) ≠ø. Получаем: yϵ f(A)^—

4)=>3) Пусть Fc__clY . Покажем, что f^-1(F)^— = f^-1(F); f^-1(F) c_ f^-1(F)^— . Покажем, что f^-1(F)^— c_ f^-1(F) f(f^-1(F)^— )c_f(f^-1(F))^—; f(f^-1(F))c_F; Fc__clY => f(^f-1(F))^— c_ F => ) f(f^-1(F)^— )c_F => f^-1(F)^— c_f^-1(F).

3)=>2) Пусть Uc_Y; Y\Uc__clY; По условию f^-1(Y\U) c__clX ; ^f-1(U)=X\ f^-1(Y\U) =>f ^-1 (U)c__op X.

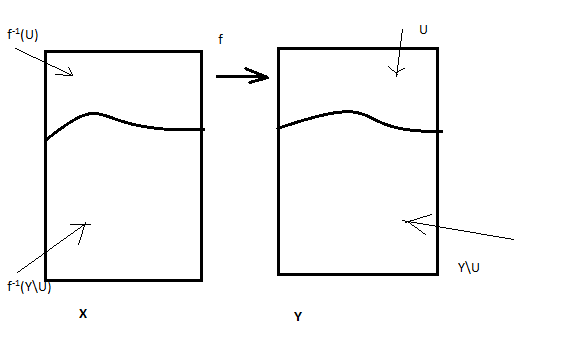
2)=>1) Рассм для любого xϵX и покажем, что f непрерывно в точке x. Рассм для любой окрестности U точку f(x). F ^-1(U)c__cl X и xϵ F ^-1(U) т.е. F ^-1(U) окрестность точки x. F(f^-1 (U))c_U

▪

18. Сужение отображение на подпространство топологического пространства и его непрерывность (2 теоремы)

Сужение непрерывного отображения на подпространство

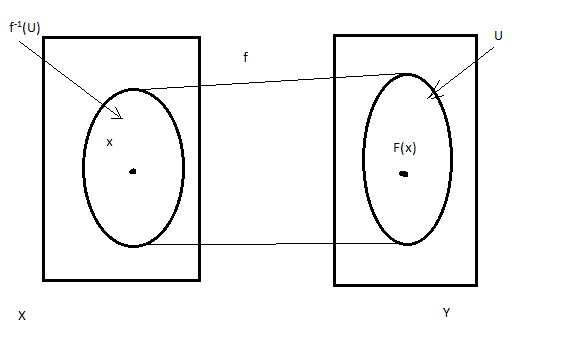
Утв1 Пусть X,Y – Т.П. f:X—>Y - непрерывное отображение, А с_Х, f(A) c_B c_Y. Тогда f_ǀA:A —>B – непрерывно.

▫ Рассм для любой точки a ϵ A. Пусть U - для любой окрестности точки f(a)в B, Ǝ окрестность Ũ точки f(a) в Yǀ Ũ∩B=U; Ǝ окрестность Ṽ точки a в X ǀf(Ṽ)c_Ũ. Пусть V=Ṽ∩A. Тогда V - окрестность точки a в A, f_ǀA(V)c_U▪

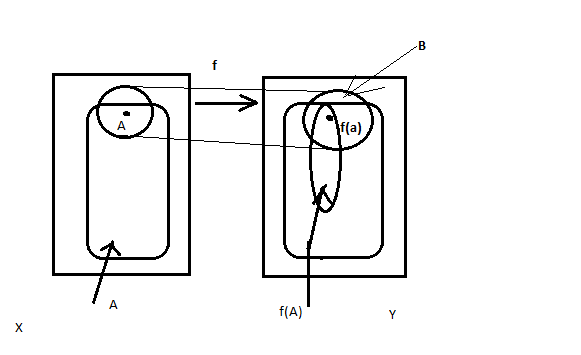
Замечание Частные случаи предыдущего утверждения:

1. f_ǀA:A —>Y – непрерывно (здесь Y=В)

2. f_ǀA:A —>f(A) – непрерывно

3. f:X—>f(X) - непрерывно

Утв2 Пусть X,Y – Т.П.; f:X—>Y - отображение

(а) Если X=F₁UF₂ …UF_n , где для любого i=1..n; F_ic__cl X и Fǀ_Fi : F_i —>Y - непрерывно, то f:X—>Y - непрерывно

(б) Если для любой точки xϵX Ǝ окрестность U_x ǀ Fǀ_Ux :U_x —>Y - непрерывно, то f - непрерывно

▫ (а) 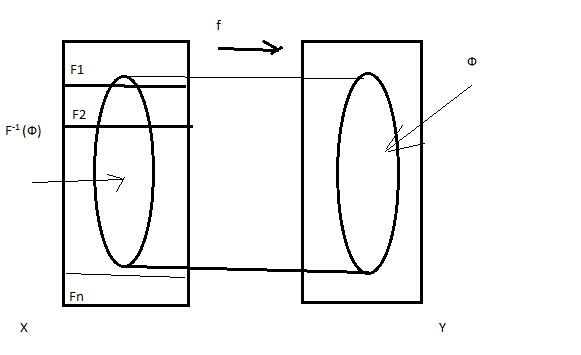Рассм для любого Фc__cl Y и покажем, что F^-1 (Ф) c__cl X. F^-1 (Ф) = (F^-1 (Ф) ∩F₁ )U..( F^-1 (Ф) ∩F_n ) для любого i=1..n F^-1 (Ф)∩F_i =(fǀ_Fi )^-1 (Ф){в конспекте не видно} F_i c__cl X => f^-1 (Ф)∩F_i c__cl X f^-1 (Ф)∩X▪