1) Если
2) Если
1)
Пусть
.
G можно представить в
виде:
2) Аналогично.
Следствие. Если топологическое пр-во X удовлетворяет 1 и 2 аксиомам счетности, то этим же свойством обладает и любое его подпространство.
13.Всюду плотные множества в топологических пространствах. Сепарабельность. Связь между сепарабельностью и второй аксиомой счетности. Пример: существование счетной базы в
Опр.: 1) пусть X-топологическое пространство, множество A X называется всюду плотным, если 1/A=X; 2)X – сепарабельно, если в X конечное или счетное всюду плотное множество.
Замечание:
пусть X
– топологическое пространство, A
X.
A
– всюду плотное в Х
точки х∈Х
∀ окрестности U
точки х U
A
.
Теорема: 1) Любое топологическое пространство, удовлетворяющее 2-ой аксиоме счетности, сепарабельно. 2) Сепарабельность метризуемого топологического пространства удовлетворяет 2-ой аксиоме счетности
1)
пусть В – конечная или счетная база в
Х. В={
|
n∈N}
∀ n∈N
fix
∈
и рассмотрим А={
},
А-не более чем счетно. Если U
открыто в Х, то U∩A≠∅, таким образом А
– всюду плотно. 2) Пусть Х-метризуемо
метрикой β и пусть А={
|n∈N}
всюду плотно в Х, рассмотрим β={
.
Рассмотрим
точку х∈Х и ∀ окрестность U точки Х.
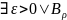(x,
)
⊆U,
выберем k∈N|
1/k<
/2,
то есть
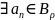(x,1/k)
⇒x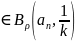
Покажем, что
,
ρ(x,
)<1/k,
ρ(
,y)<1/k
Прим.:
имеет счетную базу. (
счетная база в
Утверждение: Любое подпространство сепарабельно метризуемого пространства сепарабельно.
Пусть А – подпространство сепарабельно метризуемого пространства Х. Т.к. Х – сепарабельно и метризуемо, в Х есть счетная база⇒ в А есть счетная база ⇒А-сепарабельно.
Замечание: подпространство сепарабельно неметризуемого пространства может не быть сепарабельно.
14 . Сравнение топологий.
Опр.
: Пусть
– 2 топологии на множестве Х. Если
,
обозначается
Замечание:
отношение
сильнее
и
то
говорят, что
Бывает,
что для
и
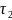не выполняется ни одно из соотношений,
тогда говорят, что они несравнимы.
Утверждение:
пусть
х
выбраны: β1
(х)
– локальная база(х,
1)
в точке х, β2
(х) – локальная база(х, τ2)
в точке х, тогда
1
2
х
Х
и
2(x)
V
β1(x)|
V
W
рассмотрим
точки
х
Х
и ∀ W∈ β2(x)
W-окрестность
точки в смысле τ1,
т.к.
β1(x)
– локальная база (х,
)в
точке х. ∃ V∈ β1(x)| V ⊆W
Рассмотрим
U⊆
τ2;
∀х∈U
∃ Wx∈
β2(x)|
Wx⊆U.
∀х∈U
fix
Vx∈
β1(x)|
Vx
⊆Wx
Vx=U (x∈U) ∀х∈U Vx∈ 1 ⇒U⊆ τ1
Cледствие: в условиях утверждения τ1=τ2 ∀ х∈Х выполняется: ∀ W∈ β2(x) ∃ V∈ β1(x)| V ⊆W и ∀ V’∈ β1(x) ∃ W’∈ β2(x)| W’⊆V’
15. Сравнение метрических топологий. Критерий топологической эквивалентности метрик
Утверждение:
пусть ρ1
и
ρ2
–
метрики на множестве Х, тогда
последовательности (xn)
от n=1
до n=
точек Х из ρ1
(хn,
x)
0
ρ2
(хn,
x)⟶0
пусть
ρ1
(хn,
x)
0,
fix
рассмотрим
шар
ρ1
(хn,
x)
0
ρ1(хn,
x)<
так как xn
xn
ρ2
(хn,
x)<
пусть
U
Покажем,
что U ∈
От противного: допустим, U
;
не
(на
х,
т.е. ρ2(хn,
x)
не
?!
Следствие:
метрики ρ1
и
ρ2
на
множестве Х порождают одну топологию
(хn)
от n=1
до n=
в Х условия ρ1
(хn,
x)
0
и ρ2(хn,
x)
равносильны.