7. Хаусдорфовы пр-ва.

Определение. Т. П. Х наз. хаусдорфовым если у любых двух различных точек этого пространства существуют непересекающиеся окрестности.

Теорема. Любое метризуемое Т. П. Х – хаусдорфово. Кроме того у любых 2-ух не пересекающихся замкнутых под-тв метризуемого про-ва Х существуют непересекающиеся окрестности .

□Пусть ρ- метрика, согл. с топологией пр-ва Х:

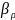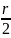1)Хаусдорфовость . Рассмотрим х,у € Х, х≠у . Пусть r=ρ(х,у) Покажем что (х , )∩ (у , )=Ø

От противного: Допустим существует z € (х , )∩ (у , ); ρ(х,у)≤ ρ(х,z)+ ρ(z,у)<r; r<r WTF!?

2)Пусть F замкн-ое под-во Х, Φ замкн под-во Х, F∩Φ= Ø ,для любого х€F, существ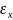ует >0 такое то (х , )∩Φ= Ø и существует >0 такое что (у , )∩F= Ø Пусть U=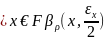 , V=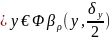 ; F под-во U,U открытое под-во Х; Φ под-во V ,V открытое под-во Х. Покажем что U∩V= Ø .От противного: Допустим существует z € U∩V => сущ x € F и y € Φ такие что z€ 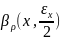∩ . Пусть тогда ρ(х,у)≤ ρ(х,z)+ ρ(z,у)≤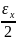 + 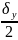≤ ; ρ(х,у)≤ ;х € )!?█

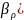Замечание: 1)Т.П. Х наз. 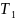-про-вом если для любого х€Х,{x} замкн в Х, любое хаусдорфаво пр-во есть пр-во.

2)Т.П. Х наз. нормальным если Х есть про-во и в любых 2-ух не пересекающихся замкнутых под-ств Х существует не пересек. окрестн. Любое метризуемое про-во не только хаусдорфово, но и нормальное.

8.Предел последовательности.

Опр. Последовательностью точек Т.П. ( Х, τ) наз отображение N→X, n--> . Запись .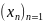

Говорят что сходится к точке х€Х для любой окрестности U точки х существует p€N такое что для любого n>p € U, где х - предел последовательности.

Зам.В хаусдорфовом ТП Х любая последовательность может иметь не более одного предела.

□От противного : Допустим →х, →у , х≠у, U,V !?

Зам. Если Т.П. Х метризуемо метрикой ρ и →х то ρ( ,х)→0

9.Замыкание мн-ва

Опр. Пусть ( Х, τ) – Т.П. А – подм-во Х. Точка х€Х наз. близкой к А, если для любой окрестности U точки х верно: U∩A≠ Ø Совокупностью всех близких к мн-ву А точек наз. замыканием мн-ва А и обозн. :

Св-ва замыкания:

1)Замыкание мн-ва А есть наименьшее по включению замкнутое мн-ва содержащее А.

□Покажем что замкнуто в Х. Рассмотрим G=X\ , пусть х € G. Существует окрестность точки х такая что U∩A≠ Ø . Покажем что U∩ ≠ Ø От противного. Допустим существует z € U∩ => U-окрестность z и z € => U∩A≠ Ø !?. Таким образом для любого х€ G существует окрестность 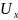являющаяся под-вом G=> Gоткрыто в Х => замкнуто в Х. Пусть A под-во F, F замкнуто в Х, Покажем что под-во F. Рассмотрим произвольную х не принадл. F. Точки U=X\F –окрестность точки х и U∩A= то есть х не принадлежит █

Следствие: пересечение всех замкнутых мн-тв содержащих А

2)А замкнуто в Х↔ =А

□=>1)очевидно<=2)А= , замкн в Х=>А замкн в Х█

3)Пусть Х-метризуемо. Тогда х€ ↔существует последовательость точек А сходящаяся к х.

□=>)х€А, для любого ε>0, (х,ε)∩A≠ для любого n€ N существует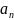 € (х,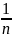 )∩A, получили последовательность такую что ρ( ,х)< => x.

<=)Рас-им для любой окр U точки х существует p€N такое что для любого p≤n, € U=>U∩A≠ Ø █

Следствие: Подмножество метризуемого праст. замкнуто ↔ когда вместе с каждой сходящейся последовательностью точек оно содержит и ее предел.

№10. Внутренность множества в топологическом пространстве и её св-ва (в том числе характеристика открытых множеств, через понятие внутренности)

Определение. Пусть 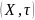-топологическое пр-во. называется внутренней т. Мн-ва A если Ǝ окрестность U т-ки 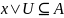. Совокупность всех внутренних точек мн-ва A называется внутренностью мн-ва A и обознач. .

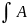Свойства: Пусть X топологическое пр-во

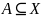
1) Внутренность A есть наибольшее по включению открытое мн-во пр-ва X содержащееся в A.

(Т.е. )

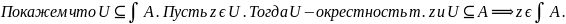
2)

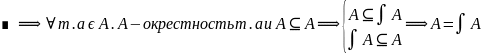
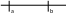Примеры:

1) Рассм.

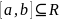
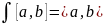
2) ) Рассм.

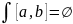
3) Рассм.

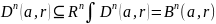
n=2

№

{Задачи.

Пусть X- топологическое пр-во подмн-ва X

2) 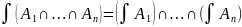}-возможно не надо

№11. Граница множества в топологическом пространстве и её св-ва (в том числе формула связывающая замыкание, внутренность и границу множества)

Определение. Пусть X-топологическое пр-во. подмн-во X. Точка называется граничной точкой множества A если окр. U т-ки x выполняется 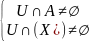. Совокупность всех границ точек мн-ва A, называется границей мн-ва A и обозначается .

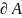Свойства границы: Пусть X топологическое пр-во

1)

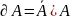
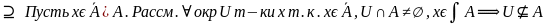
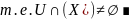
2)

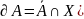
3)

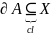
4)

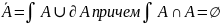
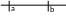Примеры:

1) Рассм.

2) Рассм. В 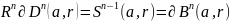n=2

№12. База топологического пр-ва. Утверждение, характеризующее базы. Локальная база пр-ва в данной точке. Первая и вторая аксиомы счётности и связь между ними. Первая аксиома счётности и метризуемость. Аксиомы счётности и подпространства.

Определение 1. Пусть -топологическое пр-во. Семейство называется базой пр-ва X, если любое непустое открытое множество можно представить в виде объединения некоторого подсемейства семейства P.

Утверждение 1. Пусть -топологическое пр-во. Семейство явл. базой пр-ва X ⇔

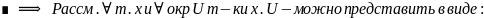
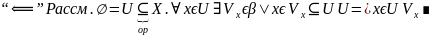
Следствие. Если топологическое пр-во X метризуемо метрикой ρ то

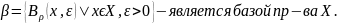
Пример:

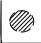
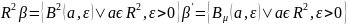
Определение 2. 1) Пусть X-топологическое пр-во, . Семейство 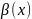- окрестностей т-ки x наз. локальной базой пр-ва X и в т.x если окр. U т-ки

2)Если в каждый т-ке пр-ва X Ǝ конечная или счётная локальная база, то говорят, что X удовлетворяет 1-ой аксиоме счётности.

Замечание. Из утверждения 1 следует, что если

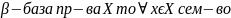
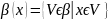явл. локальной базой пр-ва X в т-ке x.

Поэтому, если в X cущ. конечная или счётная база то X удовлетворяет 1-ой аксиоме счётности. Если в пр-ве X существует конечная или счетная база то говорят, что X удовл. 2-ой аксиоме счётности.

Пример. Рассм. ℝ. Пусть -счётно. Пок-ть что -база. Воспольз. Утв.1. Пусть

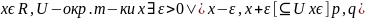
Утверждение 2. метризуемое топологическое пр-во X удовлетворяет 1-ой аксиоме счётности.

Пусть ρ-метрика, согл. с тополог. X. Рассм.

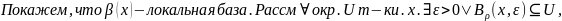
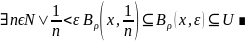
Утверждение 3. Пусть X-топологическое пр-во, A-подпр-во пр-ва X,