41 Теорема о связи между компактностью, полнотой и полной ограниченностью метрических пространств: доказательство того, что компактное метрическое пространство является полным и вполне ограниченным

Метрическое пространство (Х, ρ) компактно когда оно полное и вполне ограниченное

Доказательство:

) 1) Полнота. Пусть, - фундаментальная последовательность. Построим центрированное семейство замкнутых множеств. Обозначим: 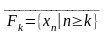. Семейство ξ= - центрированное семейство замкнутых множеств. Так как Х – компактно, то (пересечение семейств не пусто). Покажем, что . Рассмотрим ε > 0. Так как последовательность фундаментальная, то

ρ(х_n, x_m) < ε/2. Покажем, что , ρ(х_n, x) < ε. Так как В (х, ε/2). Пусть , тогда ρ (x_n,x) ρ(x_n,x_k)+ ρ(x_k,x) < ε

2) Вполне ограниченность. fix ε > 0. Рассмотрим семейство . - открытое покрытие для Х содержит конечное подпокрытие. Так как х – компактно, то х₁…х_n В (х₁, ε) .. В (х_n, ε).

42 Теорема о связи между компактностью, полнотой и полной ограниченностью метрических пространств: доказательство того, что полное и вполне ограниченное метрическое пространство компактно.

Метрическое пространство (Х, ρ) компактно когда оно полное и вполне ограниченное

Доказательство:

) «От противного». Пусть Х – некомпактно. открытое покрытие пространства Х, не содержащее конечного подпокрытия. В качестве замкнутого множества возьмем Х. Х можно представить в виде: Х = D₁ .. D_n, где D_i Х и diam D_i 1. Хотя бы одно из множеств D_i не покрывается никаким конечным подсемейством семейства . Обозначим его F₁. Строим последовательность замкнутых множеств. Построим по индукции последовательность F_i замкнутых множеств, удовлетворяющих условиям:

1) F_i F_i+1 2) F_i не покрывается никаким конечным подсемейством семейства для 3) diam F_i 1/i .

Множество F1 – определено. Пусть для k N определены F₁…F_k, которые для соответствующих значений i удовлетворяют условиям 1)-3). F_k можно представить в виде F_k= k₁ … k_m, где x_i X diam k_{i .} Хотя бы одно из этих множеств не покрываются никаким конечным подсемейством семейства . Обозначим его F_k+1. Последовательность F_i, удовлетворяющая условиям 1)-3), построена. В силу полноты . . Так как U – открыто В(х,r) U. Рассмотрим . Тогда множество F_p В(х,r) U, что противоречит условию.

43. Критерий компактности полного метрического пространства.

М.П.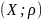 компактно <=> оно полное и вполне ограниченное.

=>) 1). Полнота

Пусть - фунд. послед. Обозначим k N . – центр. семейство замкн. мн. Т.К. Х- компактно . Покажем что .

Рассмотрим | . Покажем что . Т.к. . Пусть ,

2).Вполне огр. Fix . Рассмотрим . – открытое порк. для X. Т.к. Х- компактно | .

<=). От противн. Допустим открытое покрытие пр-ва Х не содержащее конечного подпокрытия. В силу Леммы 1 Х можно представить в виде , где . Хотя бы 1 из множеств не покр. Никаким конечным подсемейством семейства . Обозначим его . Построим последовательность замкнутых множеств, уд-х условиям:

1).

2). 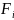не покрыто никаким конечным полсемейством семейства

3).

Множество уже определено. Пусть для опред. кот. для соотв. знач. i уровн. услов. 1-3. По лемме 1 можно представить в виде , где Хотя бы 1 из этих мн-в не покрыто никаким конечным подсемейством семейства . Обозначим его . Последовательность удовлетворяющая условиям 1-3 построена. В силу полноты последовательность .

. Рассмотрим

?!