№1. Понятие метрического пр-ва. Примеры. Шары и сферы. Ограниченные и неограниченные мн-ва в метрическом пр-ве. Диаметр мн-ва. Изометрия и изометрическое вложение.
Определение.
Пусть X
непустое мн-во, элементы которого будем
наз. точками. Метрикой на X
наз. Отображение
удовл. аксиомам:
М1)
M2)
M3)
Пара (X, ρ) называется метрическим пространством
Примеры:
ℝ
d- евклидова метрика
Радиус вектор т-ки
.
В данном случае норма вектора
d-евклидова метрика
На
существует и другие метрики
-
наибольший из катетов
-сумма
катетов
-мн-во
всех непрерывных ф-ий из [a,b]
M1)
M2)
M3)
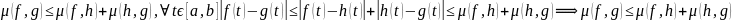
X- непустое мн-во
М3)
.
Если
-
верно неравенство. Если
Неравенство верно. δ-
дискретная метрика.
Определение.
Пусть
-метрическое
пр-во,
Открытым шаром в центре x
с радиусом r
называется мн-во
.
Замкнутым шаром в центре x
с радиусом r
наз. мн-во
.
Сферой в центре x
с радиусом r
наз. мн-во
.
Примеры:
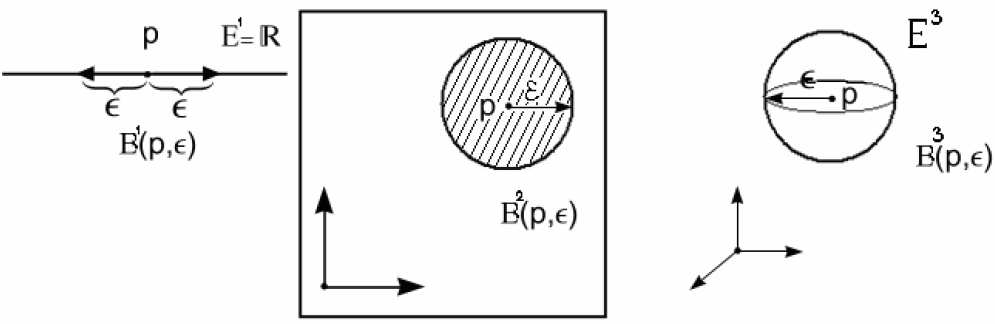
n=1 n=2 n=3
n=2
Определение.
Пусть
-топологическое
пр-во.
называется ограниченным если
.
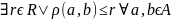Диаметром ограниченного мн-ва А называется
число
.
Если A не ограниченное то
Примеры:
Определение.
Пусть
и
метрические пр-ва. Отображение
называется изометрией, если
f-биекция
. Если существует изометрия
,
то метрики пр-ва X и
Y называется
изометричными.
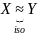
Замечание
1. Пусть
-
метрические пр-ва
Если
Если
Замечание
2. Пусть
-
метрические пр-ва. Если существует
изометрия
пр-ва
на некоторое подпр-во пр-ва
то говорят, что
изометрично вкладывается в
,
а отображение
называется изометричным вложением
в
.
№2. Топология метрического пр-ва. Открытый шар как открытое мн-во. Св-ва открытых мн-в.
Определение.
Пусть
-метрическое
пр-во.
называется открытым, если
Пустое мн-во по определению считаем
открытым. Совокупность всех открытых
мн-в метрического пр-ва
называется топологией этого пр-ва и
обозначается
.
-открытое
подмн-во пр-ва
Пример.
-
евклидова метрика.
Утверждение
1. В
метрическом пр-ве
открытый щар является открытым мн-ом.
Рассм.
.
Рассм
т.
.
Покажем, что
Рассм
Пусть
Утверждение 2.(св-ва открытых множеств) Пусть метрика пространства.
Пересечение любой конечной совокупности открытых множеств есть открытое множество.
Объединение любой совокупности открытых множеств есть открытое множество.
2) Пусть
,
где
3) Пусть
где
Терминология.
Пусть
-метрическое
пр-во,
Окрестностью
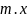будем называть любое открытое множество
содержащее эту точку.Шар
-Будем
называть -окрестностью
.
№3. Подпространство метрического пр-ва и его топология.
Определение.
Пусть
-топологическое
пр-во.
.
Обозначим через
-
сужение
на
Метрическое пр-во
-
называется подпространством метрического
пространства
.
Метрика
-называется
индуцированной метрикой.
Утверждение.
Рассм. подпространство
-метрика
пространства
.
Пусть
.
Тогда
Заметим
если
Тогда
Примеры:
Метрическое пр-во
евклидова
метрика.
-прямая
евклидова
метрика.
4. Топологические пространства. Окрестности. Метризуемые и неметризуемые пространства. Примеры метризуемого и неметризуемого пространств. Естественная топология на R^n. Понятие топологической эквивалентности метрик. Пример топологически эквивалентных метрик на R^n.
Опр. Пусть Х множество, элементы которого будем называть точками. Топологией на Х называется семейство τ подмножеств множества Х, удовлетворяющее аксиомам:
1.Ø
τ, ч
τ
2.Пересечение любой конечной совокупности множеств из τ, принадлежит τ.
3.Объединение любой совокупности множеств из τ принадлежит τ.
Опр. Пара (Х, τ) называется топологическим пространством , а множество семейства τ – открытыми множествами пространства (Х, τ).
Опр. Окрестностью точки х Х называется любое открытое множество содержащее эту точку.
Опр.
Окрестностью
множества
А
Х называется любое открытое множество
содержащее А.
U (под символом указать ор) Х – U открытое подмножество пространства Х.
Замечание
1.Любое метрическое пространство (Х, ) можно рассматривать как топологическое в следующих списках: Х наделяется топологией , порожд. метрикой .
2.Топологическое
пространство (Х,
τ) называется метризуемым,
если на Х
метрика , порождающая его топологию.
Если
метрика
-
пространство неметризуемо.
Если метрика , порождпет топологию пространства (Х, τ), то будем говорить, что согласованно с τ .
3.Метрики
,
на множестве Х называется топологически
эквивалентными, если они порождают одну
и ту же топологию
Примеры.
1)Топологию,
порожд. на R
евклидовой метрикой d
, обознач.
и называется естественной топологией
прямой R.
Пространство (R, ) обозначим R.
2)
Топологию порожденную на
евклидовой метрикой d
обозначим
и называется естественной топологией
пространства
.
Пространство (
,
)
обозначим
.
5. Замкнутые множества в топологическом пространстве и их свойства.
Опр. Пусть Х- топологическое пространство; Множество F Х называется замкнутым, если его дополнение Х\F открыто. F Х( под знаком указать cl)-F является замкнутым множеством пространства Х.
Замечание. Пусть Х- топологическое пространство F Х.
1)F
Х(
под знаком
указать cl)
F=X\U,
где U
Х(
под знаком
указать op).
2)
F
Х(
под знаком
указать cl)
т. x
F
окр. Vx
| Vx
F=Ø.
Утверждение. Пусть Х-топологическое пространство.
Свойство 1. Ø и Х замкнуты.
Свойство 2. Объединение любой конечной совокупности замкнутых множеств, является замкнутым множеством.
Свойство 3. Пересечение любой совокупности замкнутых множеств, является замкнутым множеством.
□ 1)
Ø=Х\Х, Х-открытое
Ø-замкнутое . Х=Х\Ø, Ø-открытое
Х-замкнутое.
2)
Пусть F=F1
..
Fn
, где
i
n
Fi
U
(под символом
указать ор) X.
X\F=( X\F1) .. ( X\Fn) i =1,n X\Fi U (под символом указать ор)X ( аксиома2: Пересечение любой конечной совокупности множеств из τ, принадлежит τ.) X\F (под символом указать ор) X
3 ) Пусть F= ( под знаком указать t T) Ft , где t T, Ft (под символом указать cl) X.
X\F= ( под знаком указать t T) ( X\Ft) , t T; X\Ft (под символом указать ор) Х
( аксиома3: Объединение любой совокупности множеств из τ принадлежит τ.) Х\F (под символом указать ор) Х.
Замечание 2. В любом топологическом пространстве Х, Ø и Х являются одновременно открытыми и замкнутыми множествами. Множества, которые открыты и замкнуты одновременно, называются открыто-замкнутыми.
6. Подпространства топологического пространства. Индуцированная топология. Замкнутые множества в подпространстве. Примеры: Z как подпространство R. Пример открыто-замкнутого множества в подпространстве Q прямой R.
Опр. Пусть (Х, τ) топологическое пространство , А Х – подмножество из Х. Семейство
τ/А={ u A| u τ} является топологией на А. Топологической пространство (А, τ/А ) над подпространством пространства (Х, τ) , а топология τ/А индуцированной топологией.
Таким образом u A выполняется : U А( под знаком указать op). Ũ ( под знаком указать op) Х | Ũ(u с волной) A=u.
Замечание 1 Топологическое пространство Х метризуемо метрикой ρ, то произвольное его подпространство А, метризуемо метрикой ρ /А .
Замечание 2 Пусть (Х, τ)-топологической пространство , B A X. Топология, индуцированная на В из (Х, τ) совпадает с топологией, индуцированной на В из (А, τ/А ).
Утв. Пусть Х –топологическое пространство, А-подпространство пространства Х, F A. Тогда
F
A
( под знаком
указать cl)
множество F(с
волной)
( под знаком
указать cl)
Х|
F(с волной) A=F
□
)
F
( под знаком
указать cl)A
A\F
( под знаком
указать op)
A
Ũ(u
с волной)
A=
A\F.
Пусть F( с волной)=X\ Ũ; F( с волной) ( под знаком указать cl)X и F( с волной) ) A= F.
F=
F(
с волной) )
A,
где F(
с волной)
( под знаком
указать cl)X.
Пусть Ũ
( под знаком
указать op)
и Ũ
A=A\F
A\F
( под знаком
указать op)
A
F
( под знаком
указать cl)
A
Следствие Пусть Х-топологическое пространство, А-подпространство Х, В А
Если В ( под знаком указать op) Х, то В ( под знаком указать op) А, если В ( под знаком указать cl) Х, то В ( под знаком указать cl) А.
Если В ( под знаком указать op) A, A ( под знаком указать op) X В ( под знаком указать op) X,
если В ( под знаком указать cl) A, A ( под знаком указать cl) X В ( под знаком указать cl) X.
□ 1) B A B=B A; B ( под знаком указать op) X B A ( под знаком указать op) A
2) так как В ( под знаком указать op) А; В(с волной) В ( под знаком указать op) Х|
В( с волной) А=В
В
(
под знаком
указать op)
Х
Примеры:
Z как подпространство R.
n-1 n n+1
n
;
={n}
{n}
τ 1|z=τ* - дискретная топология.
Пример открыто-замкнутого множества в подпространстве Q прямой R
Рассмотрим
пространство
как пространство
;
М=
;
М
;
М=[-
;
]
;
[-
;
]
М
;M-открыто-замкнуто
в
.