
2. Винеровский процесс.
Представьте себе мелкую частицу, взвешенную в однородной жидкости. Частица испытывает хаотические столкновения с молекулами жидкости, в результате чего она находится в непрерывном беспорядочном движении, называемым броуновским движением.
Дискретным аналогом этого процесса может служить следующая модель случайного блуждания. Частица меняет свое положение лишь в дискретные моменты времени, кратные t. Изменение положения происходит таким образом, что находясь в точке х, частица, независимо от предшествующего поведения, переходит с равными вероятностями в одну из соседних точек х+х или х-х (речь идет лишь об одной координате частицы.) В пределе t0, х0, получается непрерывное случайное движение, характерное для процесса броуновского движения.
Обозначим (t) – положение частицы в момент времени t. Пусть (0)=0. При дискретном блуждании частица за время t совершает n=t/t шагов. Пусть Sn - число шагов, совершаемых в положительном направлении.
Тогда (t)=Snх-(n- Sn)х=(2Sn-n)х.
Поскольку (0)=0, то (t)=[(t)-(s)]+ [(s)-(0)] для любого s в интервале [0,t].
В описанной модели случайного блуждания с.в. [(t)-(s)] и [(s)-(0)] являются независимыми. Причем распределение вероятностей приращения [(t)-(s)] такое же, как и приращения [(t-s)-(0)]. Поэтому
D(t)=2(t)=2(s+(t-s))=D[(t)-(s)]+D[(s)-(0)]=2(s)+2(t-s).
Следовательно, дисперсия есть линейная функция времени:
D(t)=2t,
где 2>0 - некоторая постоянная, называемая коэффициентом диффузии.
С другой стороны, дисперсия с.в. (t), описывающей смещение за n=t/t шагов, имеет вид
D(t)=D((2Sn-n)х)= D(2Snх -nх)=4(х)2DSn=(х)2n=(х)2t/t.
В итоге получаем следующее соотношение между х и t: 2=(х)2/t.
Положение частицы описывается формулой (t)=(2Sn-n)х, где Sn – число успехов в n испытаниях Бернулли.
Согласно теореме
Бернулли с.в.
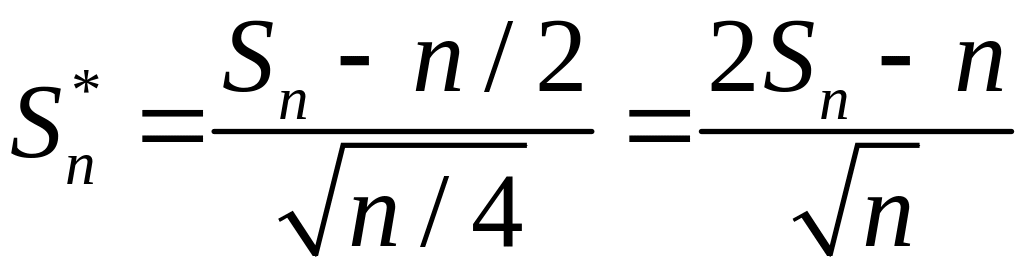 имеет стандартное нормальное распределение
и
имеет стандартное нормальное распределение
и
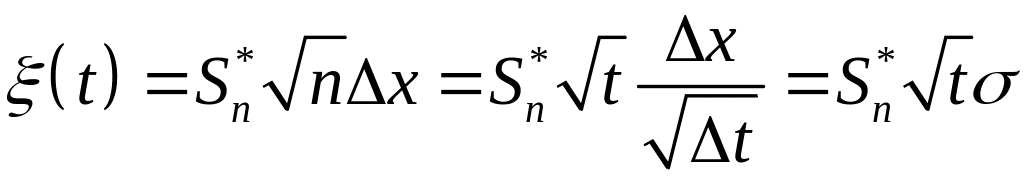 .
.
Т.О.
![]() и
и

Т.О. (t) – нормальная с.в. N(0,t2).
Т.О., для моделирования броуновского движения можно определить следующий процесс.
Определение. Винеровским процессом называется случайный процесс с независимыми приращениями, обладающий следующими свойствами:
(0)=0.
t>s с.в. [(t)-(s)] имеет нормальное распределение N(0,2(t-s)).
Моментные функции Винеровского процесса.
1. mt=0.
2. Если t>s, то
R(t,s)= M(t)(s) = M((t)-(s))(s)+M((s))2 = M((t)-(s))M(s)+M((s))2= D(s)=2s.
Если t<s, то R(t,s)=2t.
Окончательно получим R(t,s)=2min(t,s).
Т.О. корреляционные функции Пуассоновского и Винеровского процесса совпадают, но это совершенно разные процессы.
Пример на Винеровский процесс.
Пусть x – время первого достижения частицей точки х, то есть (x)=х.
Найдем распределение для с.в. x.
Если (t)х, то xt поскольку траектории частицы непрерывны.
P((t)х|xt)= P((t)х)/P(xt).
Если в момент времени x частица находилась в точке х, то далее она могла смещаться как вправо, так и влево, и поэтому могла с равной вероятностью оказаться как справа, так и слева от точки х.
Поэтому P((t)х|xt)=1/2= P((t)х)/P(xt) и
P(xt)=
P((t)х)/(1/2)=2P((t)х) .
.
Плотность вероятности с.в. x найдем, продифференцировав последнее выражение по t:
 .
.
Замечание. Винеровский процесс является представителем еще одного класса процессов, так называемых Гауссовских с.п.
Гауссовским с.п. называется процесс, у которого все распределения являются гауссовскими многомерными распределениями.
Для Винеровского процесса это очевидно выполняется, так как любое значение может быть представлено как сумма приращений, а сумма гауссовских с.в. есть гауссовская с.в.
Гауссовский и винеровские процессы имеют очень широкие области применения, включающие радиотехнику, теорию диффузии, модели шумов и.т.д.
