Лекция по случайным процессам (СП) № 1

1. Определение СП. Сечения и реализации СП. Моментные функции и их свойства.

2. СП с независимыми значениями.

3. СП с независимыми приращениями. Пуассоновский и Винеровский СП.

1. Определение сп. Сечения и реализации сп.

Не все встречающиеся на практике ситуации можно описать в терминах с.в. или случайных векторов.

Реальный эксперимент часто заключается в том, что прибор непрерывно регистрирует какую-либо характеристику и выдает ее либо в виде последовательности отсчетов через некоторые промежутки времени, либо в виде непрерывной кривой, которую рисует, например, самописец.

Если строить теоретико-вероятностную модель таких опытов, то мы придем к необходимости рассматривать одновременно бесконечное множество с.в. Это бесконечное множество может быть счетным (как последовательность отсчетов) или несчетным (как точки на непрерывной кривой).

Такого рода модели изучает теория случайных процессов. С простейшим представителем случайных процессов мы уже встречались, когда рассматривали последовательности независимых с.в. Но это самый простой случай, так как он ни имеет никакой вероятностной связи между отдельными с.в. Рассмотрим общий случай.

Определение. Пусть имеется некоторое множество Т вещественных чисел. Пусть по некоторому правилу каждому tT ставится в соответствие с.в. X_t=X_t(), определенная на некотором вероятностном пространстве (,F,P). Семейство таких с.в. X_t() называется случайной функцией X_t или случайным процессом.

Множество Т может быть счетным или несчетным. Если Т счетно, то X_t, tT называется СП с дискретным временем. Если Т несчетно, то X_t, tT называется СП с непрерывным временем.

Определенный выше СП можно рассматривать как функцию двух аргументов – числа tT и элементарного исхода .

Если зафиксировать t=t₀, то мы получим с.в. X_t0 (), которая называется сечением СП. Если зафиксировать элементарное событие =₀, то получим неслучайную функцию X_t=X_t(₀), которая называется реализацией СП.

Если рассмотреть несколько сечений СП как с.вектор , то для него существует совместная функция распределения

.

Если взять другие моменты t₁,…,t_m и другое их число, то получим другую функцию распределения.

Определение. Совокупность функций распределения сечений СП для всех n1 и любых t₁,…,t_nT называется семейством конечномерных распределений СП. Оно полностью определяет СП подобно тому как функция распределения полностью определяет с.величину или с.вектор.

Семейство конечномерных распределений обладает следующими свойствами, которые называются условиями согласования:

1. Для любой перестановки индексов (1,…,n)(k₁,…,k_n)

2. Для любых m, n, m<n

.

Кроме такой исчерпывающей характеристики как семейство конечномерных распределений используются характеристики СП, аналогичные моментам с.в. и с.векторов.

Определение. Функция

называется начальной моментной функцией k-го порядка для СП X_t (при условии, что МО в правой части существует).

Определение. Функция

₁(t)=MX_t

называется МО СП и обозначается m_t.

Определение. Функция

₁₁(t,s)=M X_tX_s

называется ковариационной функцией СП обозначается В(t,s).

Определение. Если для СП существует МО m_t, то функция

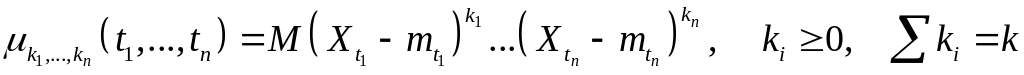
называется центральной моментной функцией k-го порядка для СП X_t (при условии, что МО в правой части существует).

Определение. Функция

называется корреляционной функцией СП X_t и обозначается R(t,s).

Легко видеть, что

R(t,s)= В(t,s)- m_tm_s.

Свойства корреляционной функции.

1. R(t,t)0tT.

2. R(t,s)=R(s,t).

3. |R(t,s)|²R(t,t)R(s,s)=DX_tDX_s, где DX_t= R(t,t) – дисперсия СП.

(Мы доказали ранее, что коэффициент корреляции по модулю меньше 1, откуда и следует свойство 3).

4. R(t,s) – положительно определенная функция, то есть для любых t₁,…,t_nT и для любых z₁,…,z_n справедливо .

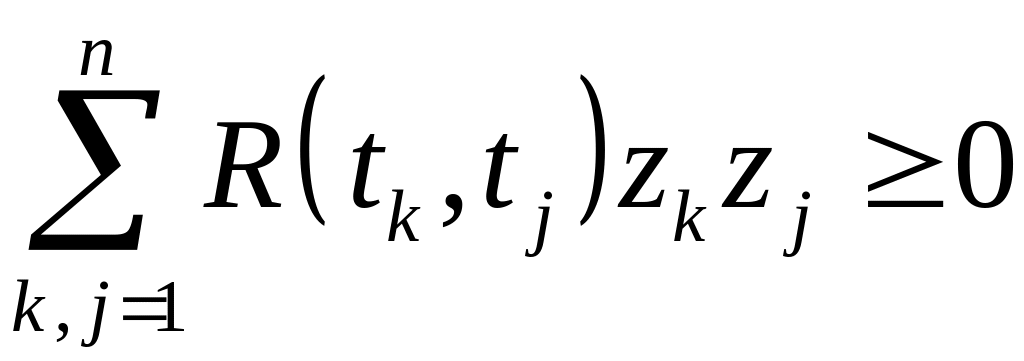Свойство 4 легко доказывается если вспомнить, что корреляционная матрица с.вектора есть положительно определенная функция.

Определение. Функция

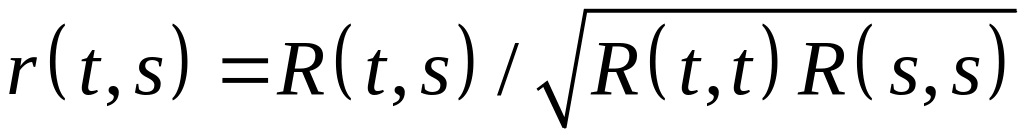
называется нормированной корреляционной функцией СП X_t.

Определение. Функция

называется взаимной корреляционной функцией СП X_t и Y_t.

Если R_XY(t,s)0, то СП X_t и Y_t называются некоррелированными.

Для комплекснозначных СП: