4. Моделирование s-образного роста

Часто поведение системы описывается S-образной или логистической кривой, показанной на рис. 7.10.

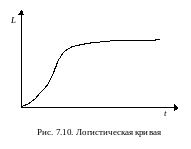
Кривая имеет два участка: начальный участок экспоненциального роста, характерный для положительной обратной связи, и участок асимптотического роста, характерный для отрицательной обратной связи. Типичным примером S-образной кривой является рост численности популяции на замкнутой территории или рост производительности однотипного оборудования по мере его амортизации. Такое поведение системы означает, что в ней сначала действует положительная обратная связь, а затем отрицательная. Диаграмма потока и уровня для простейшей системы с S-образным ростом приведена на рис. 7.11.

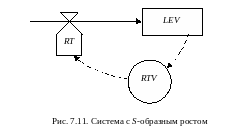
Такого рода поведение обеспечивается специальным способом определения темпа. Величина темпа задается таблично в виде функции RTV, зависящей от значения уровня LEV. На начальном участке темп нарастает, а затем уменьшается.

5. Моделирование запаздывания

В реальных системах всегда имеется запаздывание, связанное с тем, что принимаемое решение реализоваться мгновенно не может, так как все процессы в природе инерционны. Смысл запаздывания состоит в том, что любой входящий поток появляется на выходе не сразу, а через некоторое время. Типичные случаи запаздывания показаны на рис. 7.12. Для учета запаздывания в модели системной динамики вводятся специальные элементы запаздывания.

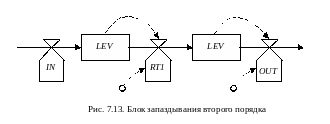
Запаздывание реализуется путем перетекания потока через ряд промежуточных резервуаров. Пример реализации блока запаздывания приведен на рис. 7.13.

6. Построение модели

Весь процесс построения модели системной динамики можно разбить на ряд этапов.

1. Анализ вербального описания моделируемой системы с целью выделения отдельных элементов и выяснения способов их взаимодействия.

2. Построение диаграммы причинно-следственных связей, определение полярностей связей и контуров причинно-следственных связей.

3. Выделение среди переменных уровней и потоков.

4. Построение на основе диаграммы причинно-следственных связей диаграммы потоков и уровней.

5. Перевод диаграммы потоков и уровней в математическую форму, т.е. написание уравнений динамики модели.

Задавая различные варианты поведения модели, меняя ее уравнения и структуру, можно изучать поведение моделируемого объекта и находить управленческие решения, приводящие объект в желаемое состояние.

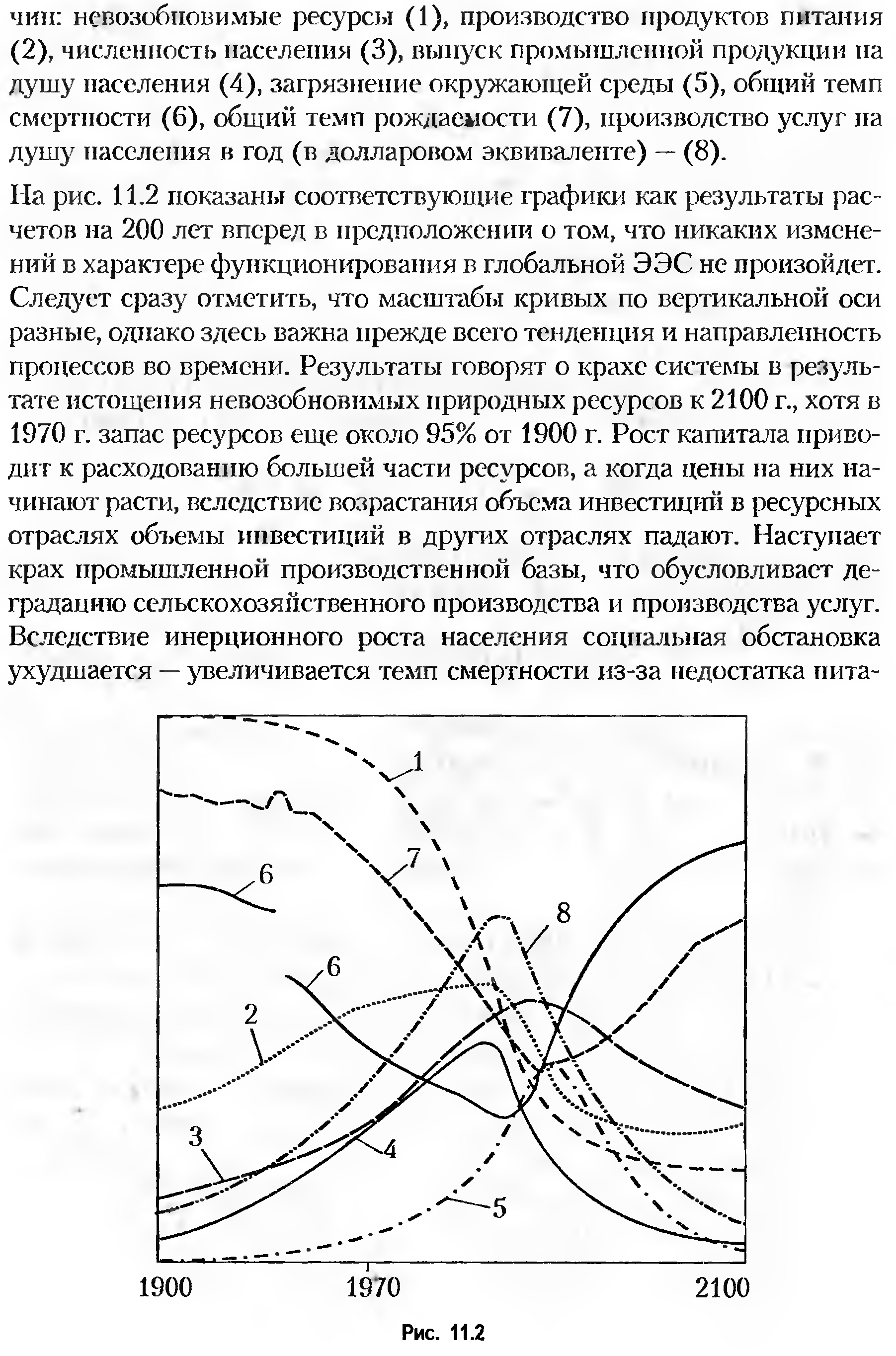
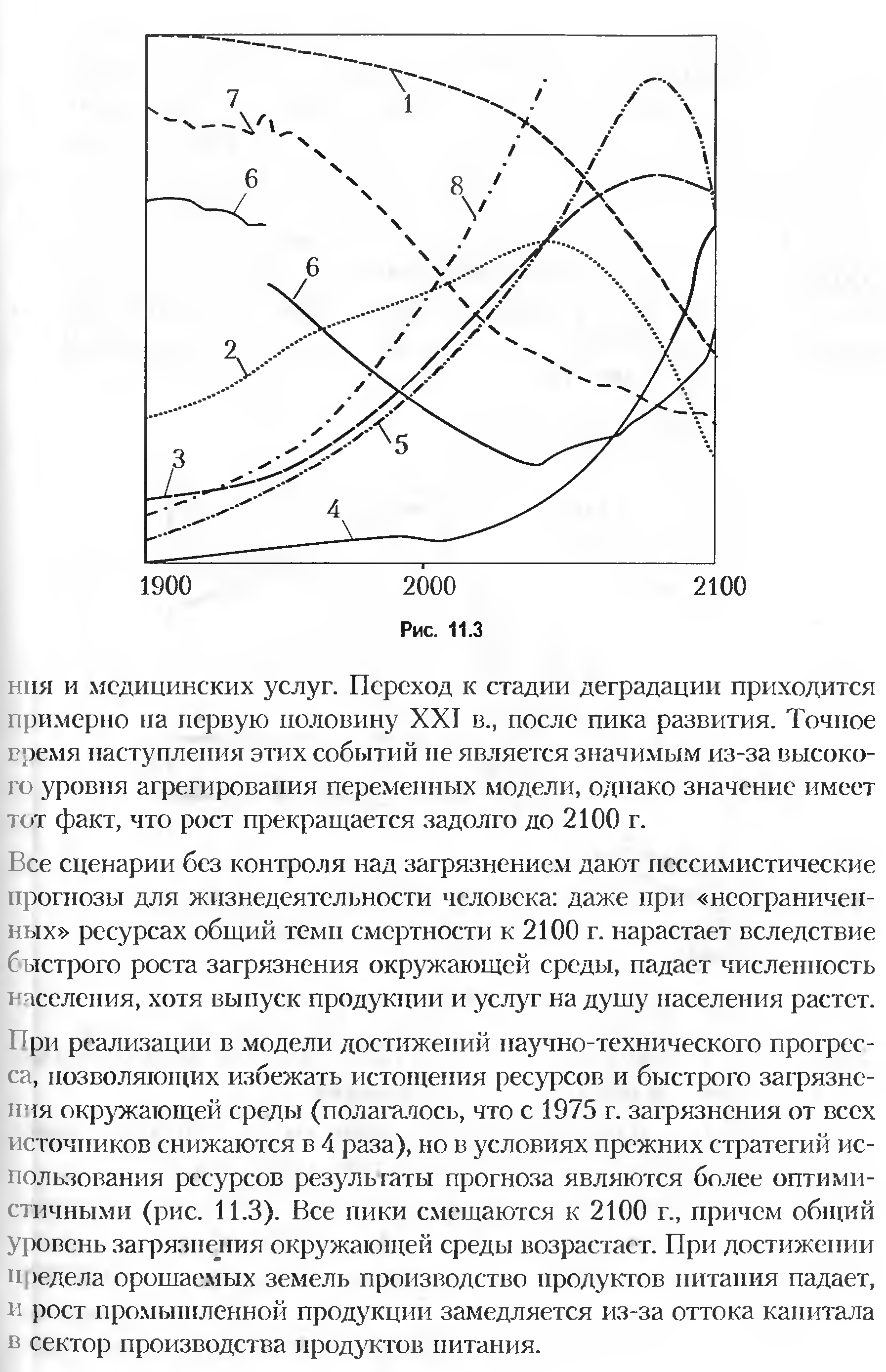
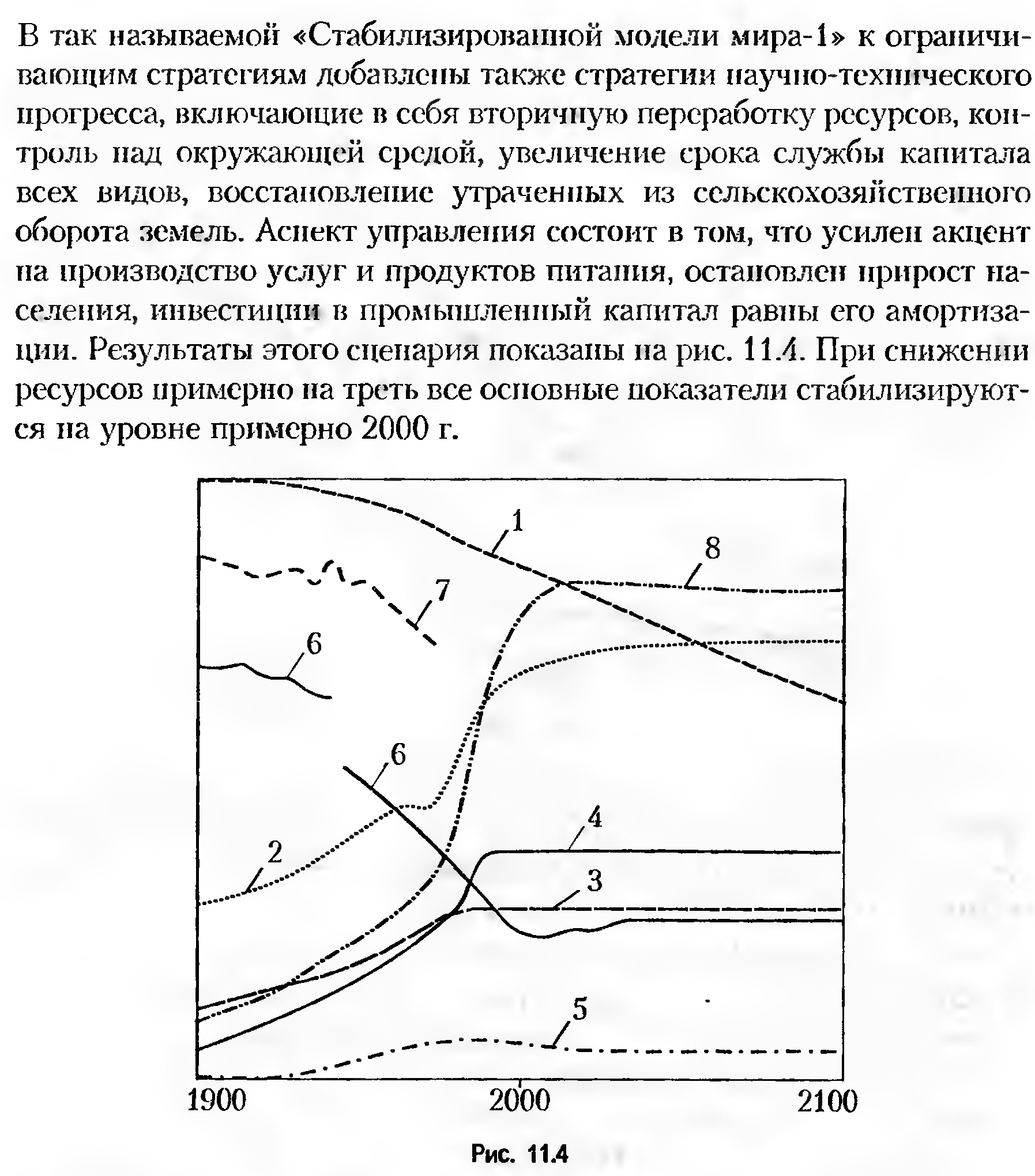
7. Модели мировой динамики

В этом пункте мы рассмотрим модели мировой динамики, предложенные Дж. Форрестером и Д. Медоузом. В основе этих моделей лежит рассмотренный выше метод системной динамики.

Структура системно-динамических моделей ЭЭС включает в себя шесть секторов: население, капиталовложения (фонды), сельскохо­зяйственные фонды, ресурсы, загрязнение и управление. Такая струк­тура была впервые предложена Дж. Форрестером и реализована в мо­дели «Мир-2».

Математическим аппаратом системной динамики являются обыкно­венные дифференциальные уравнения первого порядка. Модель «Мир-2» была построена с использованием 82 уравнений, описываю­щих взаимосвязи между элементами системы. Первоначально построе­ние и анализ системно-динамических моделей носили скорее алгорит­мический, нежели аналитический характер. Сейчас, благодаря созданию объектно-ориентированных языков программирования, стало возмож­ным создание больших моделей, включающих тысячи переменных, которые могут на достаточно достоверном уровне описывать динами­ку сложных систем.

В качестве иллюстрации приведем модель одного из шести указанных выше секторов — модель использования природных ресурсов в ре­сурсном секторе модели «Мир-3», разработанной в МГУ и включаю­щей в себя всего около 280 уравнений.

1. Пусть P_N(t) — потенциально используемые ресурсы, V_d — скорость (интенсивность) открытия новых ресурсов, V_r — скорость восстанов­ления ресурсов, зависящая от потраченных ресурсов. Тогда динамика потенциально используемых ресурсов описывается задачей Коши для дифференциального уравнения первого порядка: