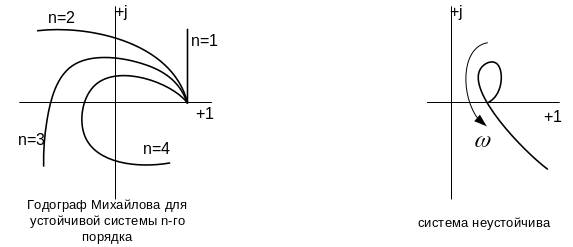4. Математическое условие устойчивости линейных систем

Как отмечалось ранее, для линейной САР общее уравнение движения может быть записано в виде:

(1)

Решением этого уравнения является:

В соответствии с определением устойчивости, система будет устойчивой, если

(2)

является решением уравнения (1) без правой части.

(3)

Каждому слагаемому в решении (4) с вещественным корнем соответствует процесс:

Каждому слагаемому в решении (4) с комплексным сопряженным корнем соответствует процесс:

Таким образом, для устойчивости САР, описываемой линейным дифференциальным уравнением (1), необходимо и достаточно чтобы все вещественные корни характеристического уравнения и все вещественные части комплексно-сопряженных корней были отрицательны. Это условие и есть математическое условие устойчивости.

Если изобразить корни на комплексной плоскости, то математическое условие устойчивости может быть сформулировано так: для устойчивости САР, описываемой линейным дифференциальным уравнением (1) необходимо и достаточно, чтобы все корни характеристического уравнения располагались слева от мнимой оси комплексной плоскости корней. Мнимая ось является в этом случае границей устойчивости.

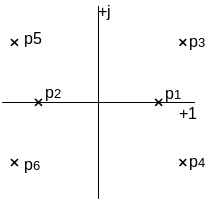
Непосредственное использование сформулированного условия возможно лишь для систем относительно невысокого порядка.

Для анализа устойчивости реальных систем используют критерии устойчивости.

5. Алгебраический критерий устойчивости Гурвица

Теорема Гурвица гласит: все корни уравнения

будут иметь отрицательные действительные части тогда и только тогда, когда все диагональные определители главного определителя положительны.

Главный определитель определяется следующим образом:

1. По главной диагонали в порядке возрастания индексов выписываются все коэффициенты от а₁ до а_n.

2. Каждая из строк дополняется влево коэффициентами с убывающими индексами, вправо – с возрастающими.

3. На месте отсутствующих коэффициентов ставятся нули.

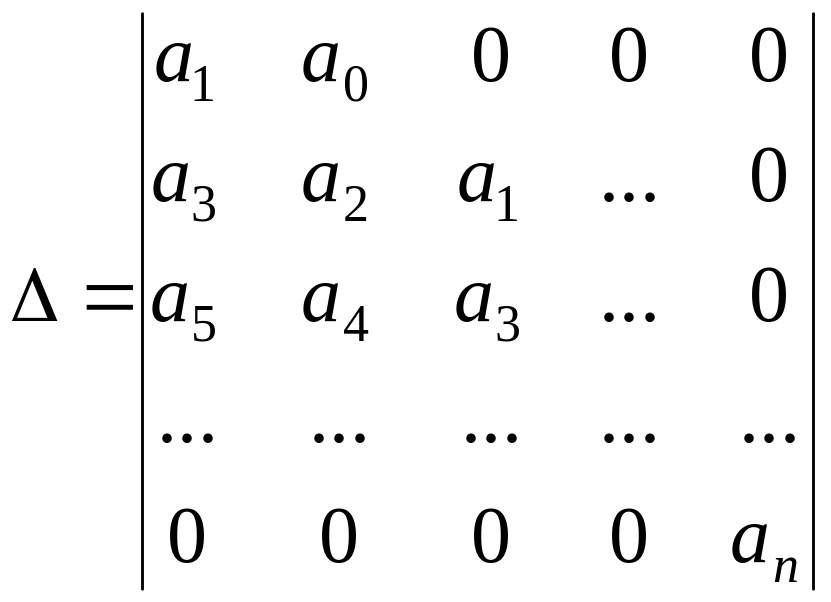
Таким образом, условием устойчивости (отрицательности действительных частей корней) по критерию Гурвица являются:

1. Все коэффициенты характеристического уравнения должны быть положительны – необходимое условие.

2. Все диагональные определители должны быть >0 – достаточное условие, то есть:

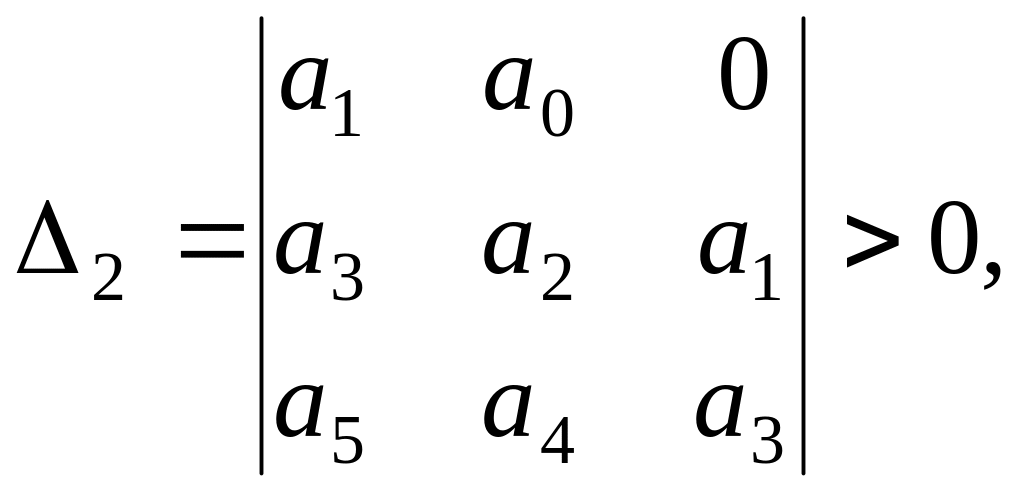
Частотный критерий устойчивости Михайлова

Заменим в полиноме А(р) на , тогда:

, где U – вещественная часть полинома ,

V – мнимая часть полинома .

На комплексной плоскости он может быть представлен в виде вектора. При изменении от до вектор своим концом опишет в комплексной плоскости кривую, которая называется годографом Михайлова или характеристической кривой. Поскольку функция является чётной функцией , а - нечётная, то годограф Михайлова симметричен относительно вещественной оси. Поэтому нет необходимости рассматривать весь годограф Михайлова, а достаточно рассмотреть лишь одну его часть, которая вычерчивает вектор при изменении от до . Тогда из уравнения (*) следует, что для установившейся системы приращение аргумента вектора при изменении от до должно быть:

Полученное выражение и есть частотный критерий устойчивости Михайлова, в математической форме. Словами его можно выразить так:

САР устойчива тогда и только тогда, когда характеристический вектор при изменении от 0 до последовательно обходит число квадрантов, равное порядку характеристического уравнения, нигде не обращается в нуль