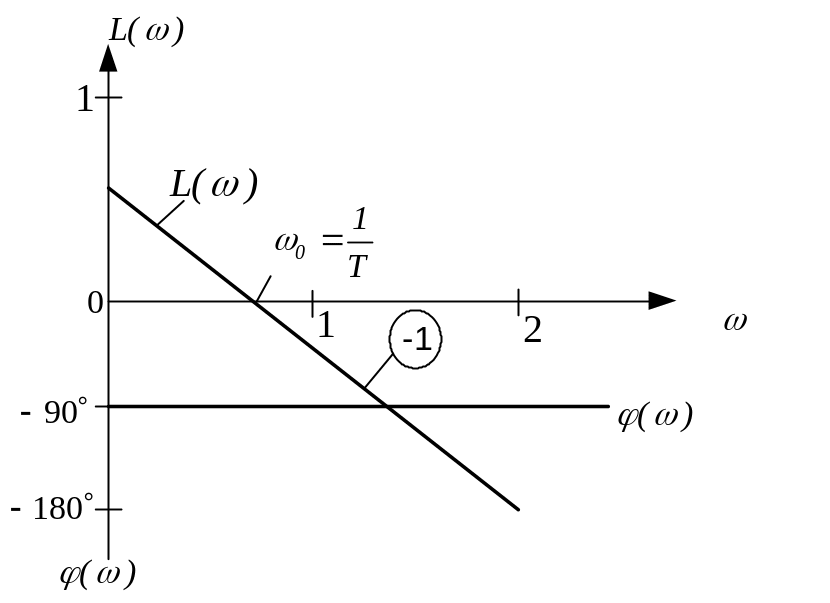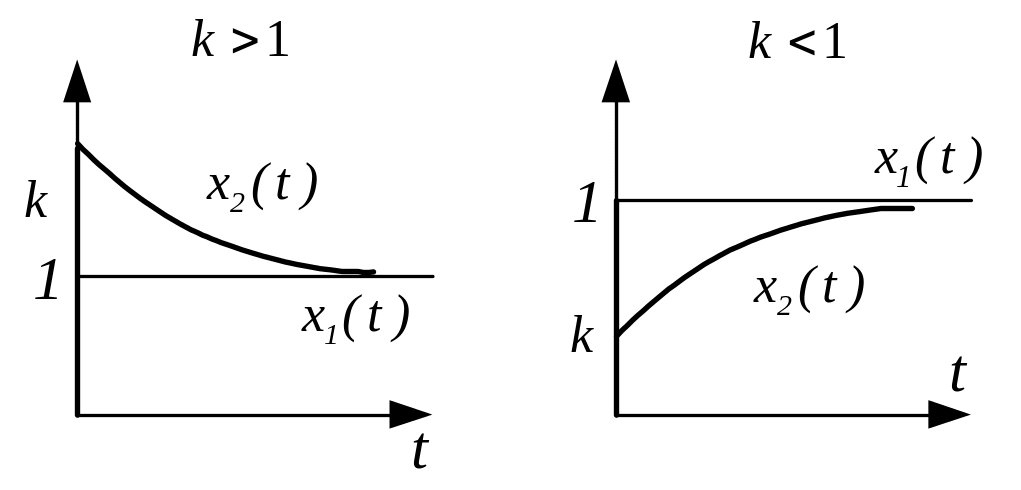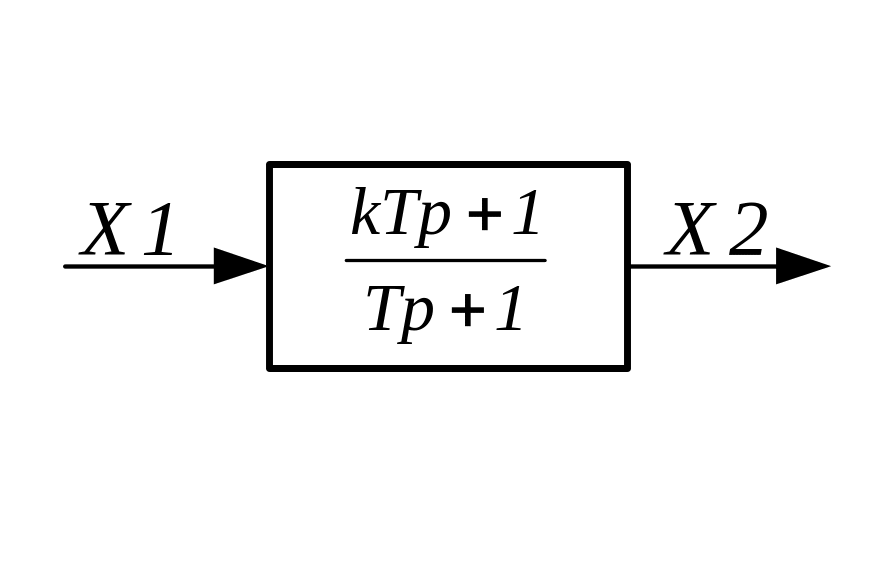- •1. Понятие о передаточной функции
- •2. Математическое описание идеальных звеньев.
- •3.Передаточные функции и чх при различных соединениях звеньев.
- •4. Математическое условие устойчивости линейных систем
- •5. Алгебраический критерий устойчивости Гурвица
- •Частотный критерий устойчивости Найквиста
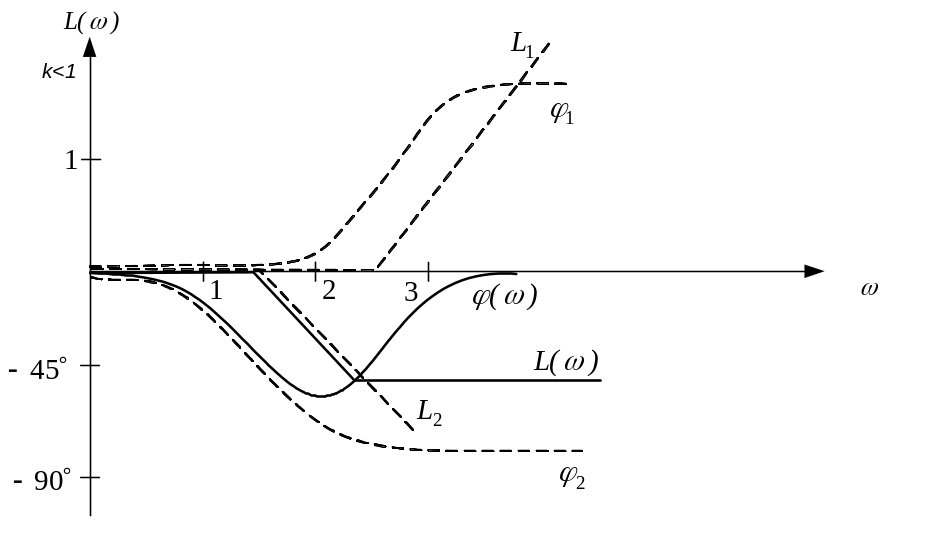
- •Критерий Найквиста можно использовать и по отношению к лчх. Согласно критерию устойчивости Найквиста сар устойчива, если при .
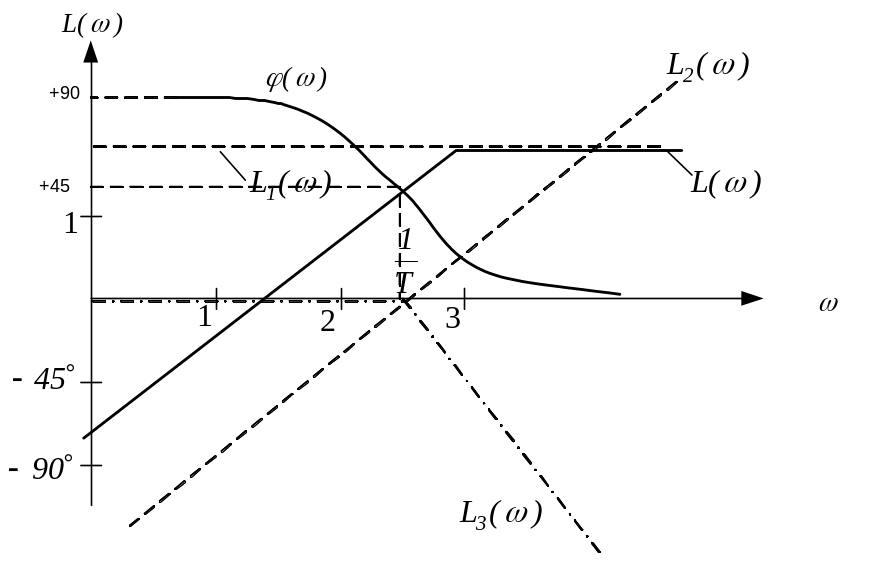
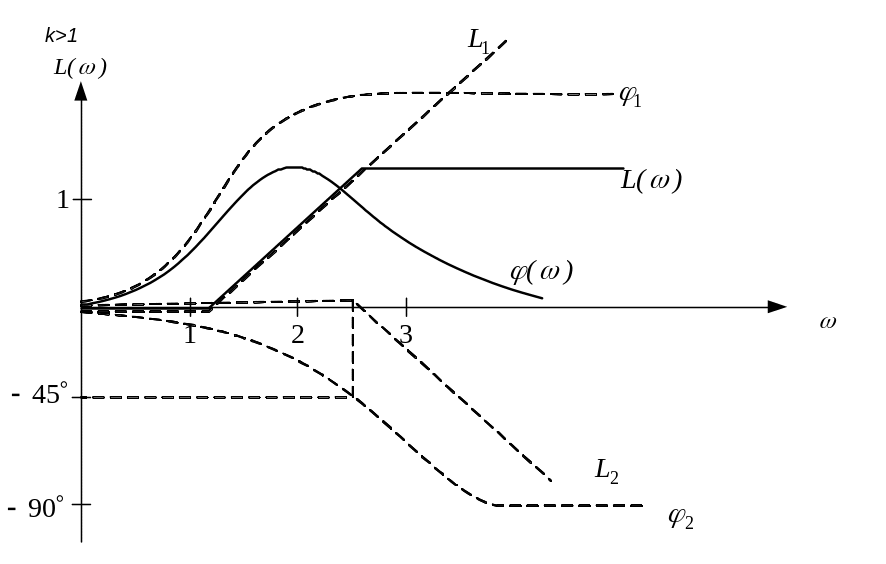
- •7. Типовые желаемые лачх.
- •Последовательная коррекция
- •Простейшими звеньями, с помощью которых обеспечивается запаздывающая коррекция сар, являются звенья с перед. Функцией вида:
- •3. Комбинированная последовательная коррекция.
- •8.Оценка качества регулирования
1. Понятие о передаточной функции

Передаточной функцией САУ по задающему воздействию называется отношение операторного изображения выходной величины САУ к операторному изображению входной величины САУ при нулевых начальных условиях, т.е.:
 .
(3)
.
(3)
Т.к. при записи уравнений линейной САУ в операторной форме дифференциальные уравнения становятся алгебраическими, то с ними можно оперировать совершенно так же, как с линейными уравнениями для установившегося режима.
![]() Обозначим
соответственно
Обозначим
соответственно
![]() ;
;
![]() - полиномы n-ой
и m-ой
степени от
р.
- полиномы n-ой
и m-ой
степени от
р.
Тогда
![]()
где Аn(р)=0 – характеристическое уравнение.
При синтезе и анализе систем используются частотные методы, для этого к уравнению (1) следует применить преобразование Фурье Для получения АФЧХ расчетным путем необходимо в передаточной функции САУ положить p = j.
![]()
Комплексная функция W(j) называется комплексным коэффициентом передачи звена или САУ или амплитудно-фазовой частотной характеристикой (АФЧХ) звена или САУ. Модуль этой функции представляет собой АЧХ, а аргумент – ФЧХ.
В общем случае W(j) может быть представлен в виде числа
![]() ,
,
где P() – называется вещественной частотной характеристикой звена или САУ (ВЧХ);
Q() – называется мнимой частотной характеристикой звена или САУ (МЧХ).
Между собой ВЧХ, МЧХ и АЧХ, ФЧХ связаны

![]()

График
![]() называется годографом - год
=
называется годографом - год
=![]()
2. Математическое описание идеальных звеньев.
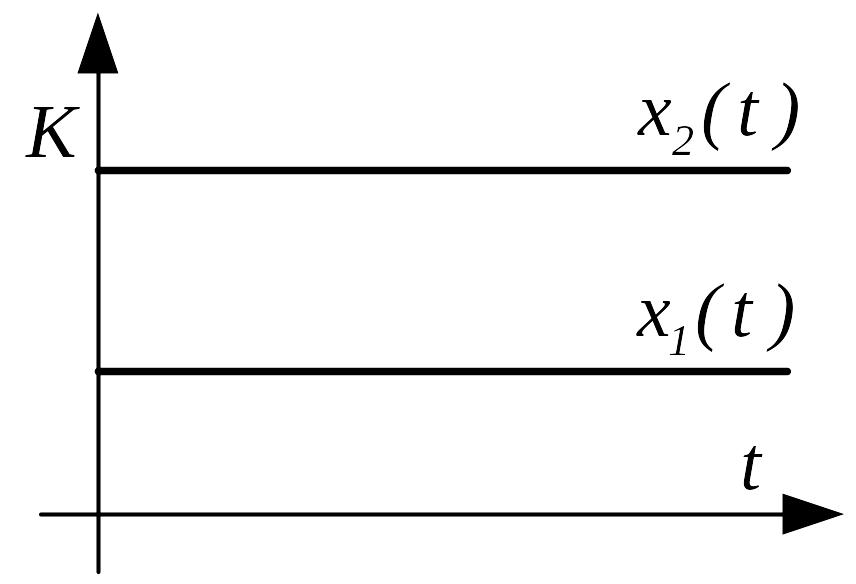
Безынерционное звено
|
x2(t) = kx1(t), в операторной форме X2(p) = kX1(p) |
|
|
Передаточная
функция Комплексный
коэффициент передачи
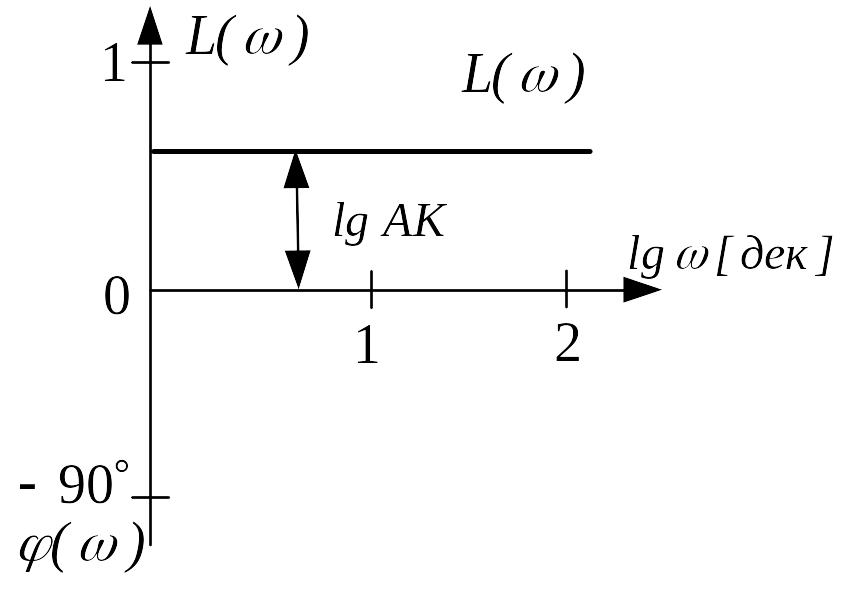
В
логарифмическом масштабе
ЛАЧХ
безинерционного звена представляет
собой прямую, параллельную оси абсцисс
и отстоящую от неё на расстоянии
|
|
Интегрирующее звено
Идеальным интегрирующим звеном называется звено, выходная величина которого пропорциональна интегралу входной величины.
![]() ;
;
![]() ,
,
|
|
|
|
|
|
|
|
|
То есть в
логарифмическом масштабе ЛАЧХ –
прямая линия. ЛАЧХ интегрирующего
звена представляет собой прямую
проходящую с наклоном
ЛФЧХ
представляет собой прямую, параллельную
оси абсцисс и отстоящую от неё на
|
||
Дифференцирующее звено
Идеальным дифференцирующим звеном называется звено, выходная величина которого пропорциональна скорости изменения входной величины.
![]() ;
; ![]() ;
;
![]() .
.
|
|
|
|
|
|
Реальные динамические звенья представляют собой соединения из элементарных звеньев.
Инерционное (апериодическое) звено 1 – го порядка
Инерционным (апериодическим) звеном 1 – го порядка называется такое звено, связь между выходом и входом определяется линейным заданным уравнением 1 – го порядка вида:
![]() ,
где Т – постоянная времени инерционного
звена. ( 1 )
,
где Т – постоянная времени инерционного
звена. ( 1 )
При ступенчатом
изменении входного сигнала
![]() и при нулевыхых условиях
и при нулевыхых условиях
![]() решение уравнения ( 1 ) может быть
представлено в виде:
решение уравнения ( 1 ) может быть
представлено в виде:
|
|
В операторной форме
![]()
|
 ;
;
.
|
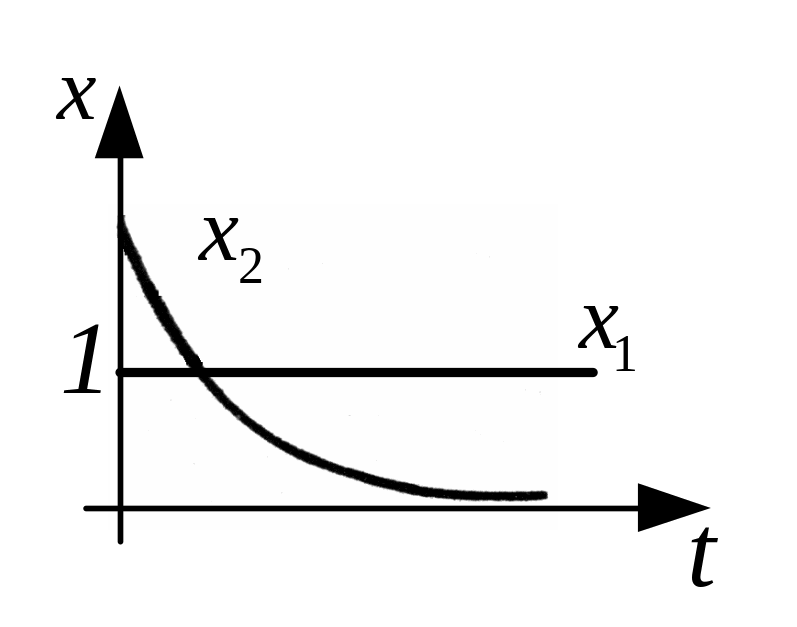
Реальное дифференцирующее звено 1 – го порядка
Это
звено, у которого связь между выходной
и входной величиной определяется
уравнением вида:
![]() ,
,
где Т – постоянная времени звена
k -эффициент усиления звена
Рассмотрим
переходный процесс в таком звене при
![]() и
и
![]()
При этих условиях решение может быть записано в виде
![]() ,
то есть при ступенчатом изменении
входного сигнала выходная величина
изменяется по экспоненциальной кривой.
,
то есть при ступенчатом изменении
входного сигнала выходная величина
изменяется по экспоненциальной кривой.
В
операционной форме
![]() ;
;
![]()
![]() ,
,
![]()
|
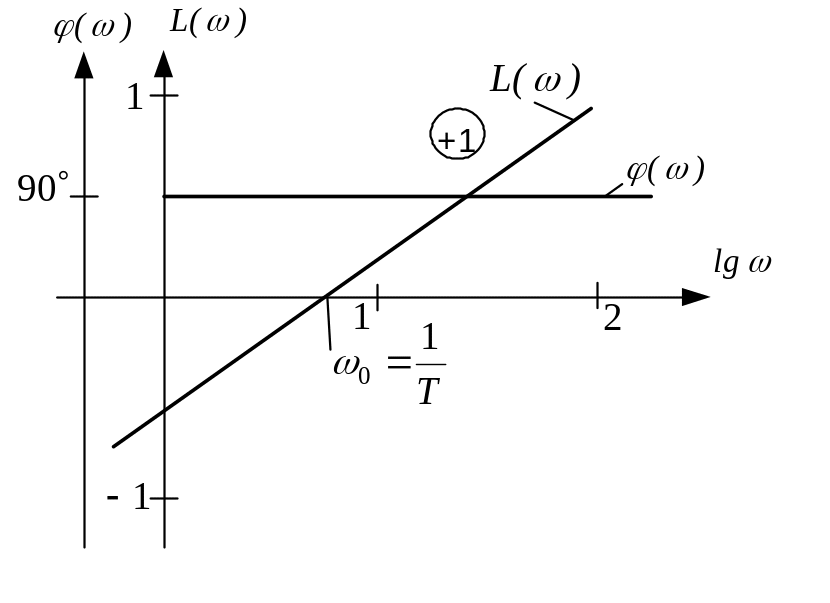
Реальное форсирующее звено 1 – го порядка
Это звено, у которого связь между выходом и входом выражается уравнением вида:
![]()
при
![]() и
и
![]()
Решение
может быть представлено в виде
![]()
при ![]()
![]()
![]()
![]()
|
В
операторной форме:
![]()
![]()
|
![]()
 ;
;![]() ,
,
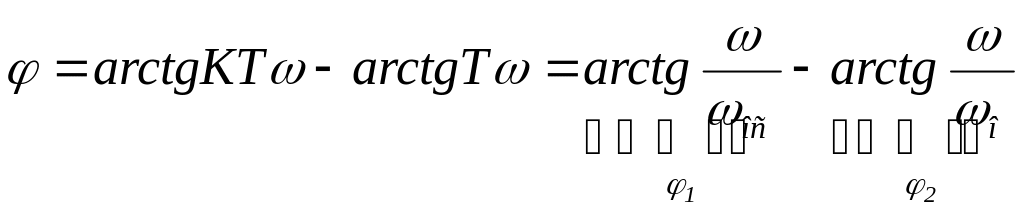
|
|