19. Дифракция Френеля на крае полуплоскости и на щели. Спираль Корню. Дифракция Фраунгофера (с помощью векторной диаграммы). Дифракционная решетка (с помощью векторной диаграммы).

Дифракция Френеля на щели. Спираль Корню.

Бесконечно длинную щель мож­но образовать, расположив рядом две обращенные в раз­ные стороны полуплоскости. Следовательно, задача о ди­фракции Френеля от щели может быть решена с помо­щью спирали Корню. Волновую поверхность падающего света, плоскость щели и экран, на котором наблюдается дифракционная картина, будем считать параллельными друг другу :

Для точки Р, лежащей против середины щели, на­чало и конец результирующего вектора находятся в сим­метричных относительно начала координат точках спи­рали (рис. 5.24). Если сместиться в точку Р', лежащую против края щели, начало результирующего вектора пе­реместится в середину спирали О. Конец вектора, переместится по спирали в направлении полюса F₁.При углублении в область геометрической тени начало и конец результирующего вектора будут скользить по спирали и в конце концов окажутся на наименьшем расстоянии друг от друга (см. на рис. вектор, соответствующий точке Р"). Интенсивность света достигнет при этом минимума. При дальнейшем скольжении по спирали начало и конец вектора снова отойдут друг от друга и интенсивность будет расти. То же самое будет происходить при смещении из точки Р в противоположную сторону, так как дифракцион­ная картина симметрична относительно середины щели.

Если изменять ширину щели, сдвигая полуплоскости в противоположные стороны, интенсивность в средней точке Р будет пульсировать, проходя попеременно через максимумы и отличные от нуля минимумы :

Итак, френелевская дифракционная картина от щели представляет собой либо светлую , либо относительно темную (в случае, изо­браженном на рис. 5.25 б) центральную полосу, по обе стороны которой располагаются симметричные относительно нее чередующиеся темные и светлые полосы.

При большой ширине щели начало и конец результиру­ющего вектора для точки Р лежат на внутренних витках спирали вблизи полюсов F₁ и F₂. Поэтому интенсивность света в точках, расположенных против щели, будет прак­тически постоянной. Только на границах геометрической тени образуется система густо расположенных узких свет­лых и темных полос.

Заметим, что все полученные в ре­зультаты справедливы при условии, что радиус когерент­ности падающей на преграду световой волны намного пре­восходит ширину щели.

.Дифракция Френеля на крае полуплоскости.

Считаем падающую волну плоской. Разобьем волновую поверхность на зоны – узкие полосы, параллельные краю полуплоскости. Их ширина d₁, d₂,… выбирается, чтобы разность хода между соседними была А. => Колебания от зон в точке Р имеют одинаковый сдвиг фаз δ.

вначале амплитуда убывает сильно, потом – слабо. Для зон, лежащих справа от Р:

=> учитывая еще и те, которые лежат слева, получим:

При ∆→0 – ломаная превратится в спираль Корню.

- интегралы Френеля.

v – отсчитывается из (0,0) по спирали. - пределы v при .

20. Естественный и поляризованный свет. Частично поляризованный свет.

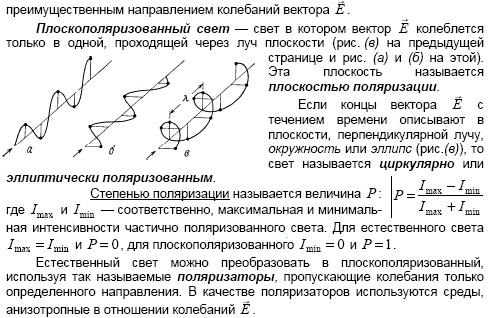
21. Поляризаторы. Степень поляризации. Поляризация при отражении и преломлении. Угол Брюстера (качественно).

22. Интерференция поляризованных лучей. Прохождение плоскополяризованного света через кристаллическую пластинку.

23. Пластинки в четверть волны и в полволны.

24. Искусственное двойное лучепреломление. Эффект Керра.

25. Вращение плоскости поляризация (естественное, магнитное). Групповая скорость. Элементарная теория дисперсии

26. Поглощение света. Закон Бугера. Коэффициент поглощения. Рассеяние света. Закон Рэлея